利用PINNs求解二维带点源泊松方程
问题描述
本案例演示如何利用PINNs方法求解二维带点源的泊松方程：
\[\Delta u = - \delta(x-x_{src})\delta(y-y_{src}).\]
其中 \((x_{src}, y_{src})\) 为点源位置对应的坐标。 点源在数学上可以用狄拉克 \(\delta\) 函数来表示：
\[\begin{split}\delta(x) = \begin{cases}
+\infty, & x = 0 \\
0, & x \neq 0
\end{cases}
\qquad
\int_{-\infty}^{+\infty}\delta(x)dx = 1.\end{split}\]
当求解域 \(\Omega=[0,\pi]^2\) 时， 二维带点源的泊松方程的解析解为：
\[u(x,y) = \frac{4}{\pi^2} \sum_{i=1}^{\infty} \sum_{j=1}^{\infty}\frac{\sin{(i x)}\sin{(i x_{src})}\sin{(j y)}\sin{(j y_{src})}}{i^2 + j^2}.\]
技术路径
MindSpore Flow求解该问题的具体流程如下：
创建训练数据集。
构建模型。
优化器。
约束。
模型训练。
模型推理及可视化。
[1]:
import time
from mindspore import context, nn, ops, jit
from mindflow import load_yaml_config
from src.dataset import create_train_dataset, create_test_dataset
from src.poisson import Poisson
from src.utils import calculate_l2_error, visual
context.set_context(mode=context.GRAPH_MODE, save_graphs=False, device_target="GPU")
# Load config
file_cfg = "poisson_cfg.yaml"
config = load_yaml_config(file_cfg)
创建数据集
本案例在求解域、边值条件、点源区域（以点源位置为中心的矩形区域）进行随机采样，生成训练数据集。具体方法见src/dataset.py。
[2]:
# Create the dataset
ds_train = create_train_dataset(config)
构建模型
本案例采用结合了sin激活函数的多尺度神经网络。
[3]:
from mindflow.cell import MultiScaleFCSequential
# Create the model
model = MultiScaleFCSequential(config['model']['in_channels'],
config['model']['out_channels'],
config['model']['layers'],
config['model']['neurons'],
residual=True,
act=config['model']['activation'],
num_scales=config['model']['num_scales'],
amp_factor=1.0,
scale_factor=2.0,
input_scale=[10., 10.],
)
约束
在利用mindflow求解PDE时，我们需要写一个mindflow.PDEWithLloss的子类来定义控制方程和边界条件分别对应的损失函数项（loss_pde和loss_bc）。因为点源区域需要加密采样点，所以我们额外增加了一个损失函数项（loss_src）。
当PINNs方法将控制方程的残差作为损失函数项来约束神经网络时，狄拉克\(\delta\)函数的奇异性使得神经网络的训练无法收敛，因此我们采用二维拉普拉斯分布的概率密度函数去近似狄拉克 \(\delta\) 函数，即：
\[\eta_{\alpha}(x, y) = \frac{1}{4\alpha^2} exp({-\frac{|x-x_{src}|+|y-y_{src}|}{\alpha}}) \qquad \underrightarrow{approx} \qquad \delta(x-x_{src})\delta(y-y_{src}).\]
其中 \(\alpha\) 为核宽度。理论上来说，只要核宽度 \(\alpha\) 充分小，那么上述概率密度函数就能很好地近似狄拉克 \(\delta\) 函数。但是实际上核宽度 \(\alpha\) 的选取对于近似效果有着重要影响。当 \(\alpha\) 太大时，概率密度函数 \(\eta_{\alpha}(x, y)\) 与狄拉克 \(\delta\) 函数之间的近似误差会变大。但如果 \(\alpha\) 太小，训练过程可能不会收敛，或者收敛后的精度可能很差。因此，\(\alpha\) 需要进行手工调参。我们这里将其确定为 \(\alpha=0.01\)。
在求解区域内、边界、点源区域均采用L2损失，并利用mindflow的MTLWeightedLoss多目标损失函数将这三个损失函数项结合起来。
[4]:
import sympy
from mindspore import numpy as ms_np
from mindflow import PDEWithLoss, MTLWeightedLoss, sympy_to_mindspore
class Poisson(PDEWithLoss):
"""Define the loss of the Poisson equation."""
def __init__(self, model):
self.x, self.y = sympy.symbols("x y")
self.u = sympy.Function("u")(self.x, self.y)
self.in_vars = [self.x, self.y]
self.out_vars = [self.u,]
self.alpha = 0.01 # kernel width
super(Poisson, self).__init__(model, self.in_vars, self.out_vars)
self.bc_nodes = sympy_to_mindspore(self.bc(), self.in_vars, self.out_vars)
self.loss_fn = MTLWeightedLoss(num_losses=3)
def pde(self):
"""Define the gonvering equation."""
uu_xx = sympy.diff(self.u, (self.x, 2))
uu_yy = sympy.diff(self.u, (self.y, 2))
# Use Laplace probability density function to approximate the Dirac \delta function.
x_src = sympy.pi / 2
y_src = sympy.pi / 2
force_term = 0.25 / self.alpha**2 * sympy.exp(-(
sympy.Abs(self.x - x_src) + sympy.Abs(self.y - y_src)) / self.alpha)
poisson = uu_xx + uu_yy + force_term
equations = {"poisson": poisson}
return equations
def bc(self):
"""Define the boundary condition."""
bc_eq = self.u
equations = {"bc": bc_eq}
return equations
def get_loss(self, pde_data, bc_data, src_data):
"""Define the loss function."""
res_pde = self.parse_node(self.pde_nodes, inputs=pde_data)
res_bc = self.parse_node(self.bc_nodes, inputs=bc_data)
res_src = self.parse_node(self.pde_nodes, inputs=src_data)
loss_pde = ms_np.mean(ms_np.square(res_pde[0]))
loss_bc = ms_np.mean(ms_np.square(res_bc[0]))
loss_src = ms_np.mean(ms_np.square(res_src[0]))
return self.loss_fn((loss_pde, loss_bc, loss_src))
# Create the problem and optimizer
problem = Poisson(model)
poisson: Derivative(u(x, y), (x, 2)) + Derivative(u(x, y), (y, 2)) + 2500.0*exp(-100.0*Abs(x - pi/2))*exp(-100.0*Abs(y - pi/2))
Item numbers of current derivative formula nodes: 3
bc: u(x, y)
Item numbers of current derivative formula nodes: 1
优化器
本案例采用Adam优化器，并在训练进行到40%、60%、80%时，学习率衰减为初始学习率的1/10、1/100、1/1000。
[5]:
n_epochs = 250
params = model.trainable_params() + problem.loss_fn.trainable_params()
steps_per_epoch = ds_train.get_dataset_size()
milestone = [int(steps_per_epoch * n_epochs * x) for x in [0.4, 0.6, 0.8]]
lr_init = config["optimizer"]["initial_lr"]
learning_rates = [lr_init * (0.1**x) for x in [0, 1, 2]]
lr_ = nn.piecewise_constant_lr(milestone, learning_rates)
optimizer = nn.Adam(params, learning_rate=lr_)
模型训练
使用MindSpore>= 2.0.0的版本，可以使用函数式编程范式训练神经网络。
[6]:
def train():
grad_fn = ops.value_and_grad(problem.get_loss, None, optimizer.parameters, has_aux=False)
@jit
def train_step(pde_data, bc_data, src_data):
loss, grads = grad_fn(pde_data, bc_data, src_data)
if use_ascend:
loss = loss_scaler.unscale(loss)
is_finite = all_finite(grads)
if is_finite:
grads = loss_scaler.unscale(grads)
loss = ops.depend(loss, optimizer(grads))
loss_scaler.adjust(is_finite)
else:
loss = ops.depend(loss, optimizer(grads))
return loss
def train_epoch(model, dataset, i_epoch):
local_time_beg = time.time()
model.set_train()
for _, (pde_data, bc_data, src_data) in enumerate(dataset):
loss = train_step(pde_data, bc_data, src_data)
print(
f"epoch: {i_epoch} train loss: {float(loss):.8f}" +
f" epoch time: {time.time() - local_time_beg:.2f}s")
for i_epoch in range(1, 1 + n_epochs):
train_epoch(model, ds_train, i_epoch)
time_beg = time.time()
train()
print(f"End-to-End total time: {time.time() - time_beg:.1f} s")
epoch: 1 train loss: 27463.34765625 epoch time: 21.84s
epoch: 2 train loss: 22351.10351562 epoch time: 12.35s
epoch: 3 train loss: 15621.81347656 epoch time: 12.36s
epoch: 4 train loss: 11910.88671875 epoch time: 12.41s
epoch: 5 train loss: 7340.56933594 epoch time: 12.45s
epoch: 6 train loss: 7032.89843750 epoch time: 12.44s
epoch: 7 train loss: 3993.34130859 epoch time: 12.46s
epoch: 8 train loss: 2885.75390625 epoch time: 12.43s
epoch: 9 train loss: 1879.61999512 epoch time: 12.40s
epoch: 10 train loss: 3002.69677734 epoch time: 12.36s
...
epoch: 241 train loss: 6.00261974 epoch time: 12.34s
epoch: 242 train loss: 6.08083344 epoch time: 12.38s
epoch: 243 train loss: 6.05793428 epoch time: 12.36s
epoch: 244 train loss: 6.05963135 epoch time: 12.36s
epoch: 245 train loss: 5.88465643 epoch time: 12.43s
epoch: 246 train loss: 6.06778002 epoch time: 12.36s
epoch: 247 train loss: 5.94315052 epoch time: 12.40s
epoch: 248 train loss: 6.28999186 epoch time: 12.44s
epoch: 249 train loss: 5.82442093 epoch time: 12.47s
epoch: 250 train loss: 5.86588335 epoch time: 12.44s
End-to-End total time: 3099.2 s
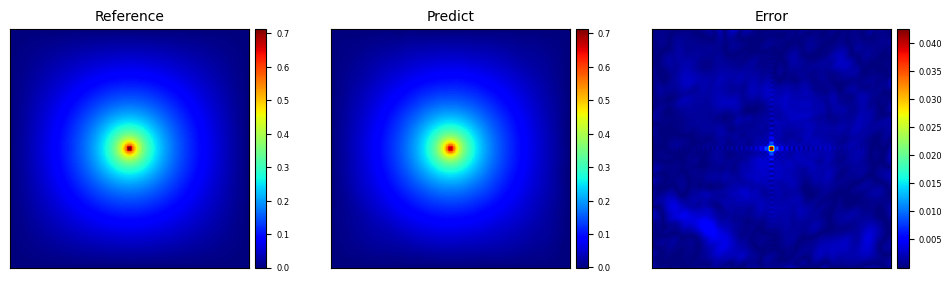
模型推理及可视化
计算相对L2误差以及绘制参考解和模型预测结果的对比图。
[7]:
from src.utils import calculate_l2_error, visual
# Create the dataset
ds_test = create_test_dataset(config)
# Evaluate the model
calculate_l2_error(model, ds_test)
# Visual comparison of label and prediction
visual(model, ds_test)
Relative L2 error: 0.0154
