AI工业流体仿真模型——东方御风

概述

“东方·御风” 是基于昇腾AI打造的面向大型客机翼型流场高效高精度AI预测仿真模型，并在昇思MindSpore流体仿真套件的支持下，有效提高了对复杂流动的仿真能力，仿真时间缩短至原来的二十四分之一，减小风洞实验的次数。同时，“东方·御风”对流场中变化剧烈的区域可进行精准预测，流场平均误差降低至万分之一量级，达到工业级标准。

本教程将对“东方·御风”的研究背景和技术路径进行介绍，并展示如何通过MindSpore Flow实现该模型的训练和快速推理，以及流场可视化分析，从而快速获取流场物理信息。

背景介绍

民用飞机气动设计水平直接决定飞机的“四性”，即安全性，舒适性，经济性，环保性。飞机的气动设计作为飞机设计中最基础，最核心的技术之一，在飞机飞行包线（起飞-爬升-巡航-下降-降落等）的不同阶段有着不同的研究需求和重点。如起飞阶段工程师将更关注外部噪声和高升阻比，而巡航阶段则关注油耗效率和能耗效率。流体仿真技术在飞机的气动设计的应用广泛，其主要目的在于通过数值计算的方法获取仿真目标的流场特性（速度、压力等），进而分析飞机的气动性能参数，实现飞行器的气动性能的优化设计。

目前，飞行器的气动仿真通常采用商业仿真软件对流体的控制方程进行求解，得到相应的气动性能参数（升阻力，压力，速度等）。无论基于何种CFD的仿真软件，都包含以下几个步骤：

物理建模：将物理问题抽象简化，对相关几何体的2D/3D的流体和固体计算域进行建模。
网格划分：将计算域划分为相应大小的面/体积单元，以便解析不同区域不同尺度的湍流。
数值离散：将流体控制方程中的积分，微分项，偏导项通过不同阶的数值格式离散为代数形式，组成相应的代数方程组。
流体控制方程求解：利用数值方法（常见的如SIMPLE算法，, PISO 算法等）对离散后的控制方程组进行迭代求解，计算离散的时间/空间点上的数值解。
流场后处理：求解完成后，使用流场后处理软件对仿真结果进行定性和定量的分析和可视化绘图，验证结果的准确性。

然而，随着飞机设计研制周期的不断缩短，现有的气动设计方法存在诸多局限。为使大型客机的气动设计水平赶超波音和空客两大航空巨头，必须发展先进的气动设计手段，结合人工智能等先进技术，建立适合型号设计的快速气动设计工具，进而提高其对复杂流动的仿真能力，减少风洞试验的次数，降低设计研发成本。

在飞行器的设计中，机翼的阻力分布约占整体飞行阻力的52%，因此，机翼形状设计对飞机整体的飞行性能而言至关重要。然而，三维翼型高精度CFD仿真需划分成百上千万量级的计算网格，计算资源消耗大，计算周期长。为了提高仿真设计效率，通常会先针对三维翼型的二维剖面进行设计优化，而这个过程往往需要对成千上万副的翼型及其对应工况进行CFD的重复迭代计算。其中，超临界翼型在高速巡航阶段的有着重要的应用。因为相较于普通翼型，超临界翼型的头部比较丰满，降低了前缘的负压峰值，使气流较晚到达声速，即提高了临界马赫数；同时，超临界翼型上表面中部比较平坦，有效控制了上翼面气流的进一步加速，降低了激波的强度和影响范围，并且推迟了上表面的激波诱导边界层分离。因此，超临界翼型有着更高的临界马赫数，可大幅改善在跨音速范围内的气动性能，降低阻力并提高姿态可控性，是机翼形状中必须考虑的设计。

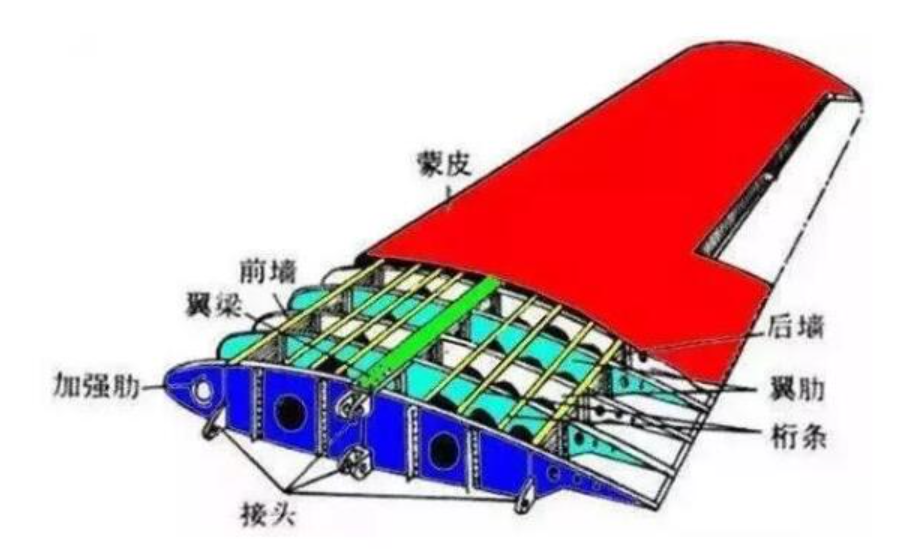
然而，二维超临界翼型的气动设计需要针对不同的形状参数和来流参数进行仿真，依然存在大量的重复迭代计算工作，设计周期长。因此，利用AI天然并行推理能力，缩短设计研发周期显得尤为重要。基于此，商飞和华为联合发布了业界首个AI工业流体仿真模型– “东方·御风” ，该模型能在超临界翼型的几何形状、来流参数（攻角/马赫数）发生变化时，实现大型客机翼型流场的高效高精度推理，快速精准预测翼型周围的流场及升阻力。

技术难点

为了实现超临界翼型的的AI高效高精度流场预测，需要克服如下的技术难点：

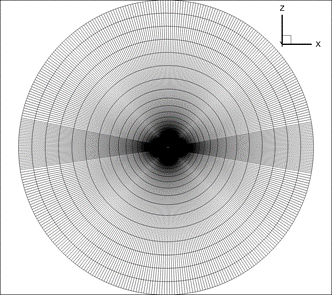
翼型网格疏密不均，流动特征提取困难。 二维翼型计算域的流体仿真网格常采用O型或C型网格。如图所示，为典型的O型网格剖分。为了精准地计算流动边界层，对翼型近壁面进行了网格加密，而来流远场的网格则相对稀疏。这种非标的网格数据结构增加了提取流动特征的困难程度。
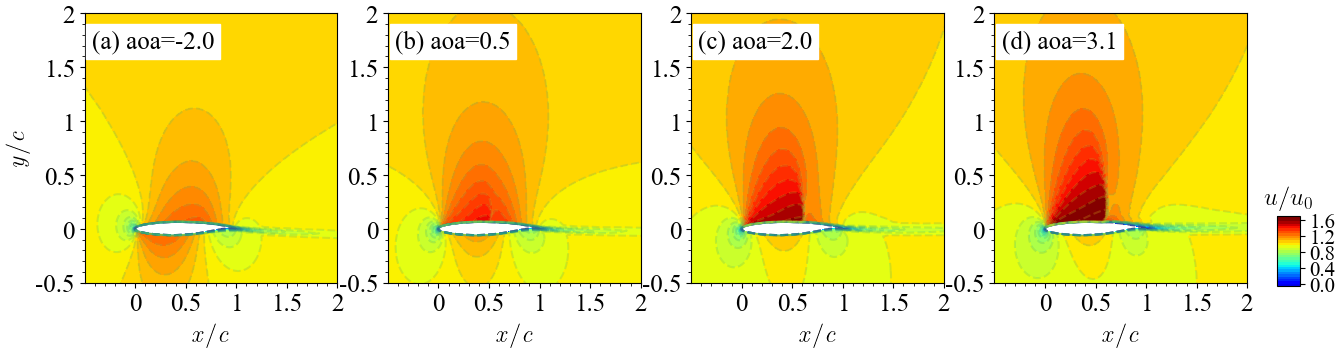
不同气动参数或翼型形状发生改变时，流动特征变化明显。 如图所示，当翼型的攻角发生变化时，流场会发生剧烈的变化，尤其当攻角增大到一定程度时，会产生激波现象：即流场中存在明显的间断现象，流体在波阵面上的压力、速度和密度形成明显的突跃变化。
激波区域流场变化剧烈，预测困难。 由于激波的存在对其附近的流场影响显著，激波前后的流场变化剧烈，流场变化复杂，导致AI预测困难。激波的位置直接影响着翼型的气动性能设计和载荷分布。因此，对激波信号的精准捕捉是十分重要但充满挑战的。

技术路径

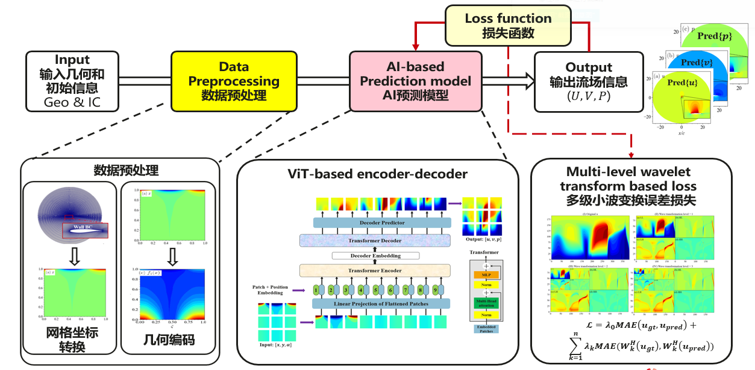
针对如上所述的技术难点，我们设计了基于AI模型的技术路径图，构建不同流动状态下翼型几何及其对应流场的端到端映射，主要包含以下几个核心步骤：

首先，设计AI数据高效转换工具，实现翼型流场复杂边界和非标数据的特征提取，如图数据预处理模块。先通过曲线坐标系网格转换程序实现规则化AI张量数据生成，再利用几何编码方式加强复杂几何边界特征的提取。
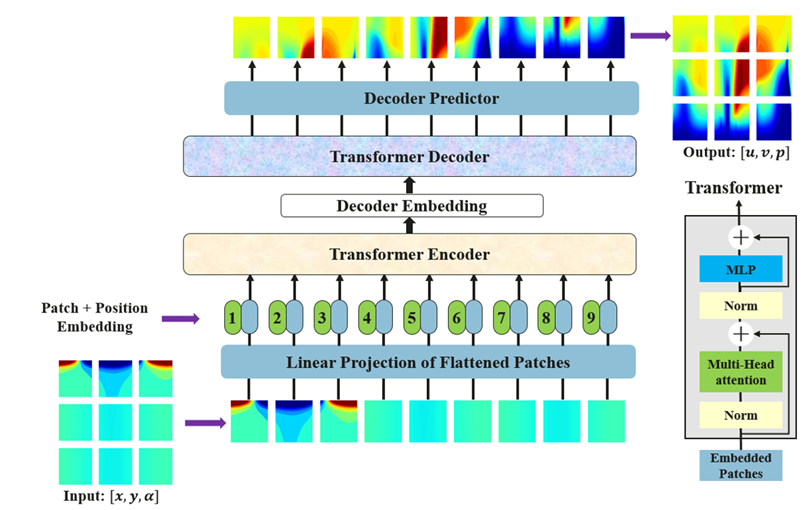
其次，利用神经网络模型，实现不同流动状态下翼型构型和流场物理量的映射，如图ViT-based encoder-decoder所示；模型的输入为坐标转换后所生成的翼型几何信息和气动参数；模型的输出为转换后生成的流场物理量信息，如速度和压力。
最后，利用多级小波变换损失函数训练网络的权重。对流场中突变高频信号进行进一步地分解学习，进而提升流场剧烈变化区域（如激波）的预测精度，如图loss function对应的模块；

准备环节

实践前，确保已经正确安装最新版本的MindSpore与MindSpore Flow。如果没有，可以通过：

MindSpore安装页面安装MindSpore。
MindSpore Flow安装页面安装MindSpore Flow。

“东方·御风”MindSpore Flow实现

“东方·御风”MindSpore Flow实现分为以下6个步骤：

配置网络与训练参数
数据集制作与加载
模型构建
模型训练
结果可视化
模型推理

[1]:

import os
import time
import numpy as np

import mindspore.nn as nn
import mindspore.ops as ops
from mindspore import context
from mindspore import dtype as mstype

from mindspore import save_checkpoint, jit, data_sink
from mindspore import set_seed

from mindflow.common import get_warmup_cosine_annealing_lr
from mindflow.pde import SteadyFlowWithLoss
from mindflow.loss import WaveletTransformLoss
from mindflow.cell import ViT
from mindflow.utils import load_yaml_config

以下src文件可以在applications/data_driven/airfoil/2D_steady/src中下载。

[2]:

from src import AirfoilDataset, calculate_eval_error, plot_u_and_cp, get_ckpt_summ_dir

set_seed(0)
np.random.seed(0)

context.set_context(mode=context.GRAPH_MODE,
                    save_graphs=False,
                    device_target="Ascend",
                    device_id=6)
use_ascend = context.get_context("device_target") == "Ascend"

配置网络与训练参数

从配置文件中读取四类参数，分别为模型相关参数（model）、数据相关参数（data）、优化器相关参数（optimizer）、输出相关参数（ckpt）、验证相关参数（eval）。您可以从config获取这些参数。

[3]:

config = load_yaml_config("config.yaml")
data_params = config["data"]
model_params = config["model"]
optimizer_params = config["optimizer"]
ckpt_params = config["ckpt"]
eval_params = config["eval"]

数据集制作与加载

数据集下载地址：data_driven/airfoil/2D_steady/dataset

数据为mindrecord类型文件，读取和查看数据形状的代码如下：

[4]:

mindrecord_name = "flowfiled_000_050.mind"
dataset = ds.MindDataset(dataset_files=mindrecord_name, shuffle=False)
dataset = dataset.project(["inputs", "labels"])
print("samples:", dataset.get_dataset_size())
for data in dataset.create_dict_iterator(num_epochs=1, output_numpy=False):
    input = data["inputs"]
    label = data["labels"]
    print(input.shape)
    print(label.shape)
    break

该文件包含2808个流场数据，为51个超临界翼型在Ma=0.73和不同攻角范围内（-2.0~4.6）的流场数据。其中，input的数据维度为（13, 192, 384），192和384为经过雅格比转换后的网格分辨率，13为不同的特征维度，分别为(\(AOA\), \(x\), \(y\), \(x_{i,0}\), \(y_{i,0}\), \(\xi_x\), \(\xi_y\), \(\eta_x\), \(\eta_y\), \(x_\xi\), \(x_\eta\), \(y_\xi\), \(y_\eta\))。

Label的数据维度为（288，768），可以经过utils.py中的patchify 函数(16×16)操作后所得的流场数据（u,v,p），可以通过utils.py中的unpatchify操作还原成（3, 192, 384），用户可根据自身网络输入输出设计进行个性化配置和选择。

首先将CFD的数据集转换成张量数据，然后将张量数据转换成MindRecord。设计AI数据高效转换工具，实现翼型流场复杂边界和非标数据的特征提取，转换前后的x，y和u的信息如下图所示。

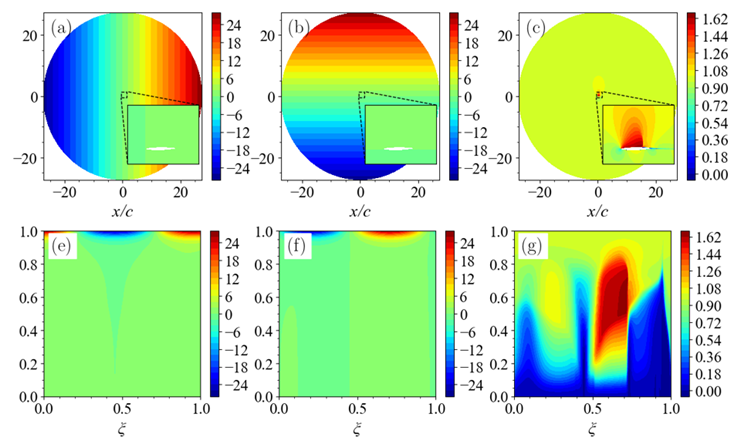
AI流体仿真目前支持使用本地数据集训练，通过MindDataset接口可以配置相应数据集选项，需要指定MindRecord数据集文件位置。

config.yaml中的“train_size”字段默认为0.8，表示在“train”模式下训练集和验证集的默认比例为4:1，用户可自定义修改；config.yaml中的“finetune_size”默认为0.2，表示在“finetune”模式下训练集和验证集的默认比例为1:4，用户可自定义修改；训练模式设置为“eval”时，数据集全部作为验证集。

config.yaml中的“min_value_list”字段和“min_value_list”字段分别表示攻角、几何编码后x信息、几何编码后y信息的最大和最小值。 config.yaml中的“train_num_list”字段和“test_num_list”字段分别表示训练和验证所对应的数据集翼型起始编号列表，每组数据包含50个翼型数据，例如“train_num_list”字段为[0]，表示训练集为0-49所对应的50个翼型数据。

[5]:

method = model_params['method']
batch_size = data_params['batch_size']
model_name = "_".join([model_params['name'], method, "bs", str(batch_size)])
ckpt_dir, summary_dir = get_ckpt_summ_dir(ckpt_params, model_name, method)
max_value_list = data_params['max_value_list']
min_value_list = data_params['min_value_list']
data_group_size = data_params['data_group_size']
dataset = AirfoilDataset(max_value_list, min_value_list, data_group_size)

train_list, eval_list = data_params['train_num_list'], data_params['test_num_list']
train_dataset, eval_dataset = dataset.create_dataset(data_params['data_path'],
                                                     train_list,
                                                     eval_list,
                                                     batch_size=batch_size,
                                                     shuffle=False,
                                                     mode="train",
                                                     train_size=data_params['train_size'],
                                                     finetune_size=data_params['finetune_size'],
                                                     drop_remainder=True)

model_name: ViT_exp_bs_32
summary_dir: ./summary_dir/summary_exp/ViT_exp_bs_32
ckpt_dir: ./summary_dir/summary_exp/ViT_exp_bs_32/ckpt_dir
total dataset : [0]
train dataset size: 2246
test dataset size: 562
train batch dataset size: 70
test batch dataset size: 17

模型构建

这里以ViT模型作为示例，该模型通过MindSpore Flow的模型定义的ViT接口构建，需要指定ViT模型的参数。您也可以构建自己的模型。其中ViT模型最重要的参数为encoder和decoder的depth、embed_dim和num_heads，分别控制模型中layer数、隐向量的长度以及多头注意力机制的头数。具体参数配置含义默认值如下：

[7]:

if use_ascend:
    compute_dtype = mstype.float16
else:
    compute_dtype = mstype.float32
model = ViT(in_channels=model_params[method]['input_dims'],
            out_channels=model_params['output_dims'],
            encoder_depths=model_params['encoder_depth'],
            encoder_embed_dim=model_params['encoder_embed_dim'],
            encoder_num_heads=model_params['encoder_num_heads'],
            decoder_depths=model_params['decoder_depth'],
            decoder_embed_dim=model_params['decoder_embed_dim'],
            decoder_num_heads=model_params['decoder_num_heads'],
            compute_dtype=compute_dtype
            )

损失函数与优化器

为了提升对流场高低频信息的预测精度，尤其是改善激波区域的误差，我们使用多级小波变换函数wave_loss作为损失函数，其中wave_level可以确定使用小波的级数，建议可以使用2级或3级小波变换。在网络训练的过程中，我们选取了Adam。

[8]:

# prepare loss scaler
if use_ascend:
    from mindspore.amp import DynamicLossScaler, all_finite, init_status
    loss_scaler = DynamicLossScaler(1024, 2, 100)
else:
    loss_scaler = None
steps_per_epoch = train_dataset.get_dataset_size()
wave_loss = WaveletTransformLoss(wave_level=optimizer_params['wave_level'])
problem = SteadyFlowWithLoss(model, loss_fn=wave_loss)
# prepare optimizer
epochs = optimizer_params["epochs"]
lr = get_warmup_cosine_annealing_lr(lr_init=optimizer_params["lr"],
                                    last_epoch=epochs,
                                    steps_per_epoch=steps_per_epoch,
                                    warmup_epochs=1)
optimizer = nn.Adam(model.trainable_params() + wave_loss.trainable_params(), learning_rate=Tensor(lr))

训练函数

使用MindSpore>= 2.0.0的版本，可以使用函数式编程范式训练神经网络，单步训练函数使用jit装饰。数据下沉函数data_sink，传入单步训练函数和训练数据集。

[6]:

def forward_fn(x, y):
    loss = problem.get_loss(x, y)
    if use_ascend:
        loss = loss_scaler.scale(loss)
    return loss

grad_fn = ops.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=False)

@jit
def train_step(x, y):
    loss, grads = grad_fn(x, y)
    if use_ascend:
        status = init_status()
        loss = loss_scaler.unscale(loss)
        if all_finite(grads, status):
            grads = loss_scaler.unscale(grads)
    loss = ops.depend(loss, optimizer(grads))
    return loss

train_sink_process = data_sink(train_step, train_dataset, sink_size=1)

模型训练

模型训练过程中边训练边推理。用户可以直接加载测试数据集，每训练n个epoch后输出一次测试集上的推理精度。

[7]:

print(f'pid: {os.getpid()}')
print(f'use_ascend : {use_ascend}')
print(f'device_id: {context.get_context("device_id")}')

eval_interval = eval_params['eval_interval']
plot_interval = eval_params['plot_interval']
save_ckt_interval = ckpt_params['save_ckpt_interval']
# train process
for epoch in range(1, 1+epochs):
    # train
    time_beg = time.time()
    model.set_train(True)
    for step in range(steps_per_epoch):
        step_train_loss = train_sink_process()
    print(f"epoch: {epoch} train loss: {step_train_loss} epoch time: {time.time() - time_beg:.2f}s")
    # eval
    model.set_train(False)
    if epoch % eval_interval == 0:
        calculate_eval_error(eval_dataset, model)
    if epoch % plot_interval == 0:
        plot_u_and_cp(eval_dataset=eval_dataset, model=model,
                      grid_path=data_params['grid_path'], save_dir=summary_dir)
    if epoch % save_ckt_interval == 0:
        ckpt_name = f"epoch_{epoch}.ckpt"
        save_checkpoint(model, os.path.join(ckpt_dir, ckpt_name))
        print(f'{ckpt_name} save success')

pid: 71126
use_ascend : True
device_id: 6
total dataset : [0]
train dataset size: 2246
test dataset size: 562
train batch dataset size: 70
test batch dataset size: 17
model_name: ViT_exp_bs_32
summary_dir: ./summary_dir/summary_exp/ViT_exp_bs_32
ckpt_dir: ./summary_dir/summary_exp/ViT_exp_bs_32/ckpt_dir
epoch: 1 train loss: 2.855625 time cost: 99.03s
epoch: 2 train loss: 2.7128317 time cost: 11.67s
epoch: 3 train loss: 2.5762033 time cost: 11.34s
epoch: 4 train loss: 2.4458356 time cost: 11.62s
epoch: 5 train loss: 2.3183048 time cost: 11.35s
...
epoch: 996 train loss: 0.07591154 time cost: 10.27s
epoch: 997 train loss: 0.07530779 time cost: 10.57s
epoch: 998 train loss: 0.07673213 time cost: 11.10s
epoch: 999 train loss: 0.07614599 time cost: 10.56s
epoch: 1000 train loss: 0.07557951 time cost: 10.25s
================================Start Evaluation================================
mean l1_error : 0.00028770750813076604, max l1_error : 0.09031612426042557, average l1_error : 0.015741700749512186, min l1_error : 0.002440142212435603, median l1_error : 0.010396258905529976
mean u_error : 0.0003678269739098409, max u_error : 0.1409306526184082, average u_error : 0.02444652929518591, min u_error : 0.002988457679748535, median u_error : 0.018000304698944092
mean v_error : 0.0001693408951670041, max v_error : 0.025479860603809357, average v_error : 0.0065298188753384985, min v_error : 0.0011983513832092285, median v_error : 0.005558336153626442
mean p_error : 0.0003259546544594581, max p_error : 0.11215704679489136, average p_error : 0.016248753842185524, min p_error : 0.0014863014221191406, median p_error : 0.009315729141235352
mean Cp_error : 0.0004100774693891735, max Cp_error : 0.052939414978027344, average Cp_error : 0.00430003712501596, min Cp_error : 0.0008158683776855469, median Cp_error : 0.0018098950386047363
=================================End Evaluation=================================
predict total time: 27.737457513809204 s
================================Start Plotting================================
./summary_dir/summary_exp/ViT_exp_bs_32/U_and_Cp_compare.png
================================End Plotting================================
Plot total time: 27.499852657318115 s
Train epoch time: 122863.384 ms, per step time: 1755.191 ms
epoch_1000.ckpt save success

结果可视化

翼型几何形状发生改变时，AI和CFD预测的表面压力分布，流场分布及其误差统计如下：

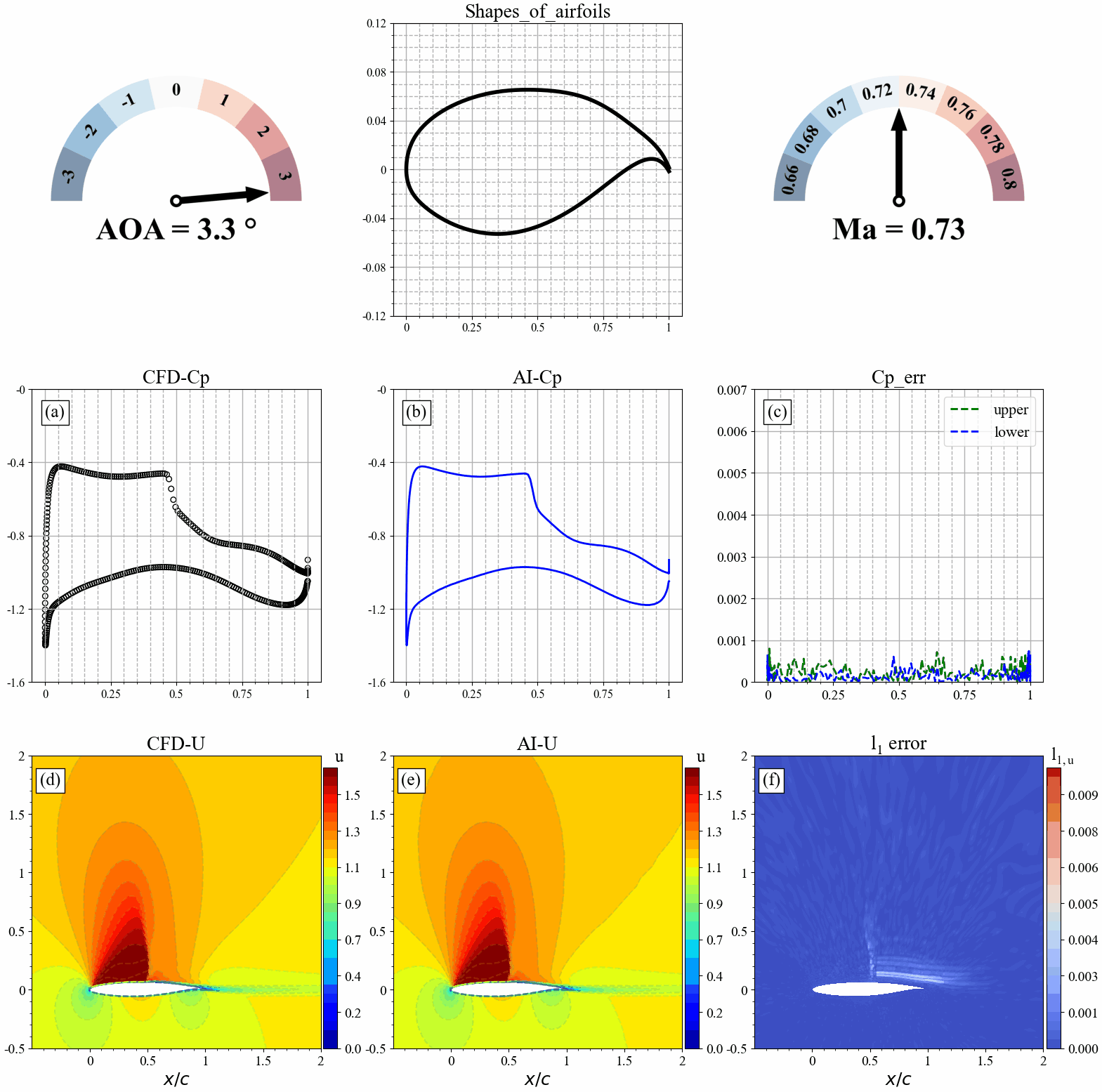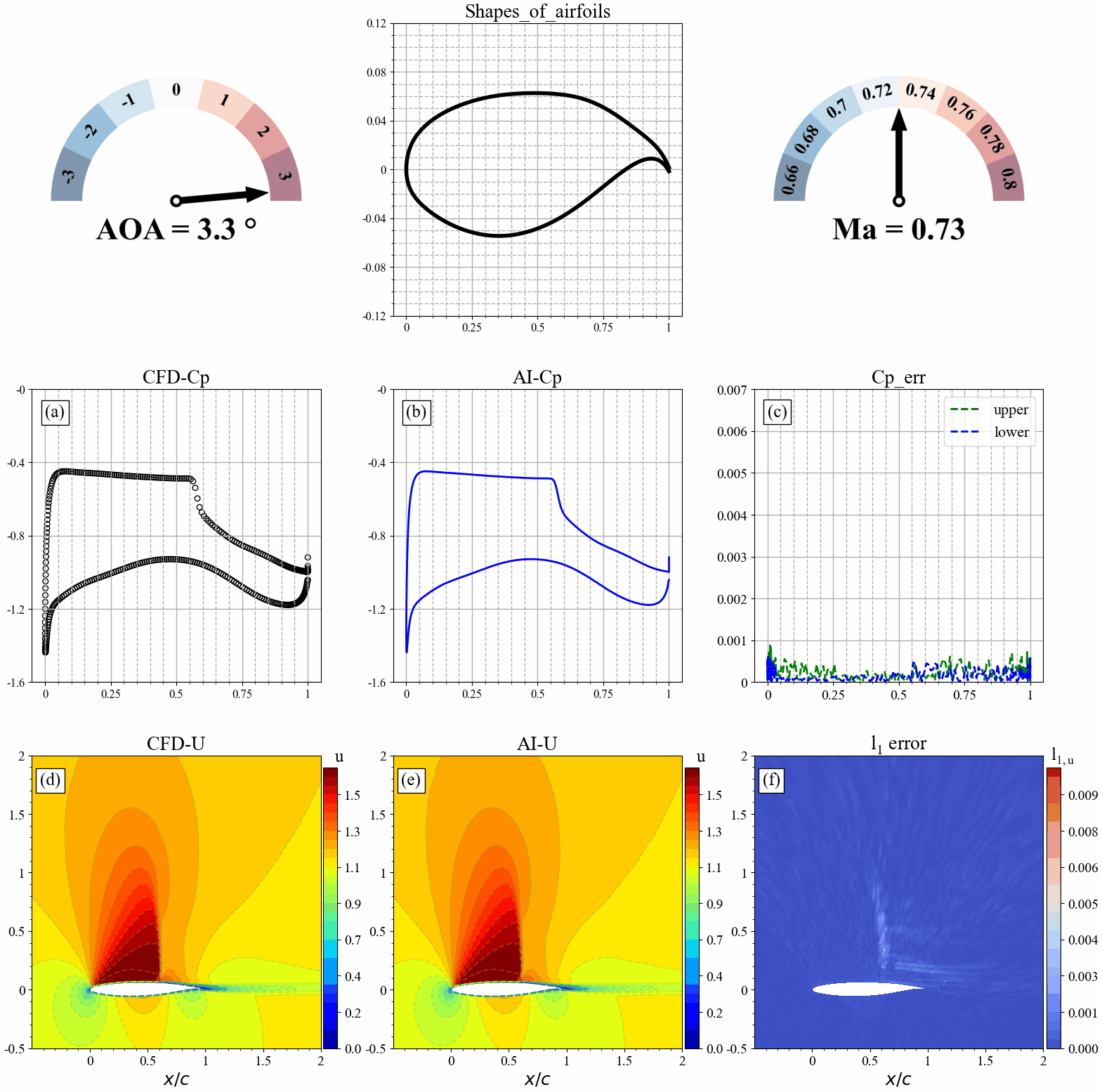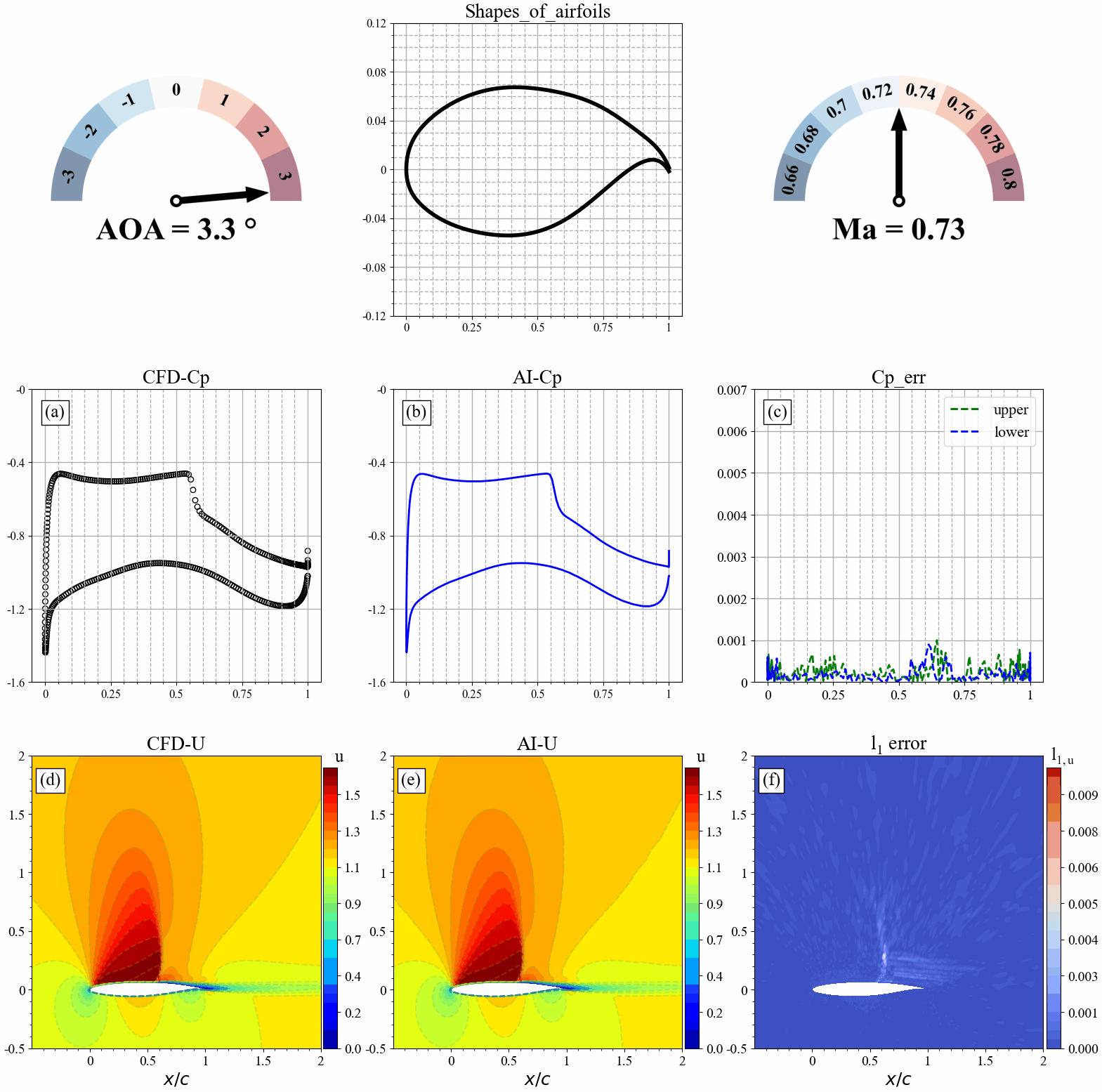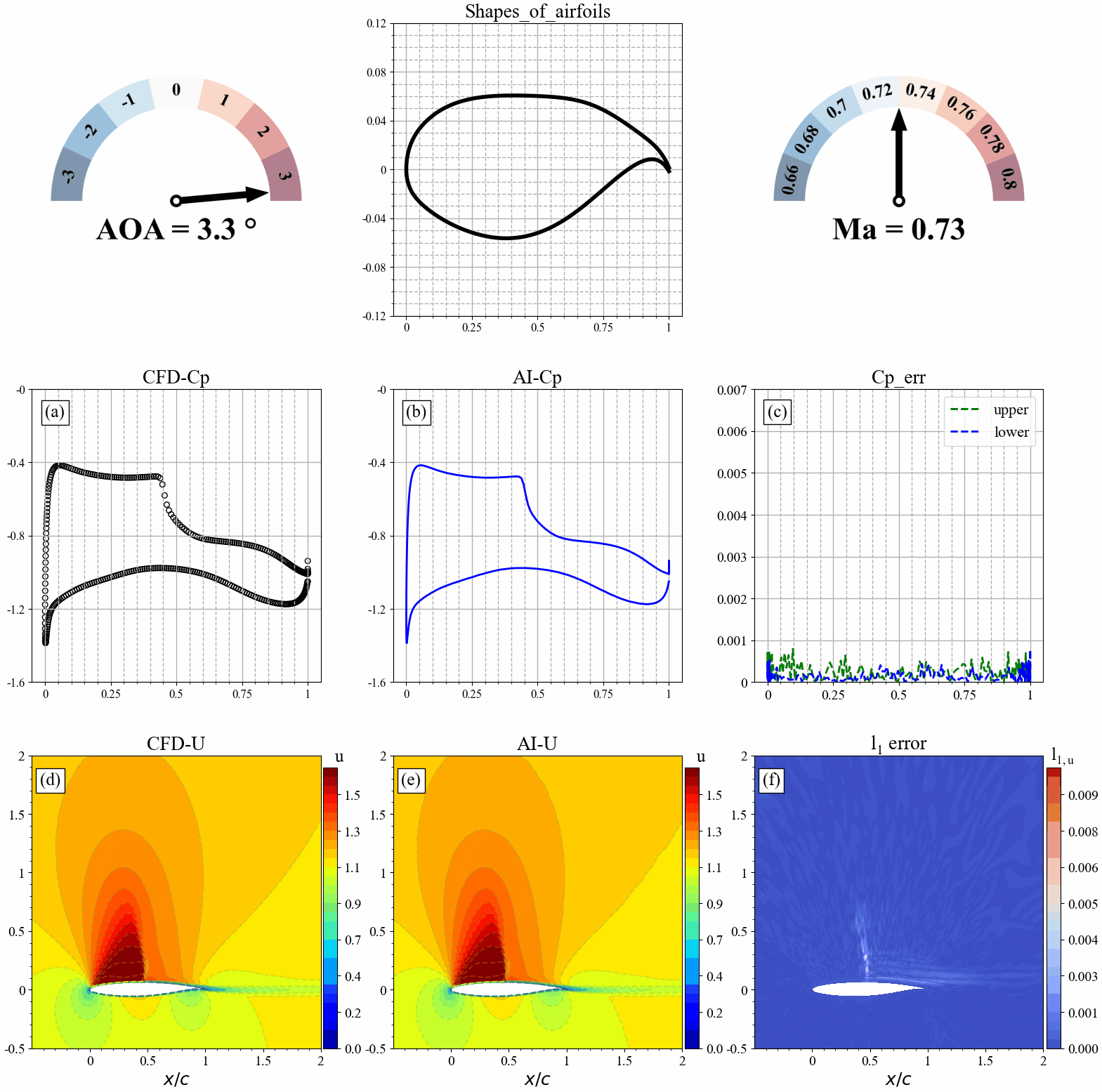
来流攻角发生改变时，AI和CFD预测的表面压力分布，流场分布及其误差统计如下：

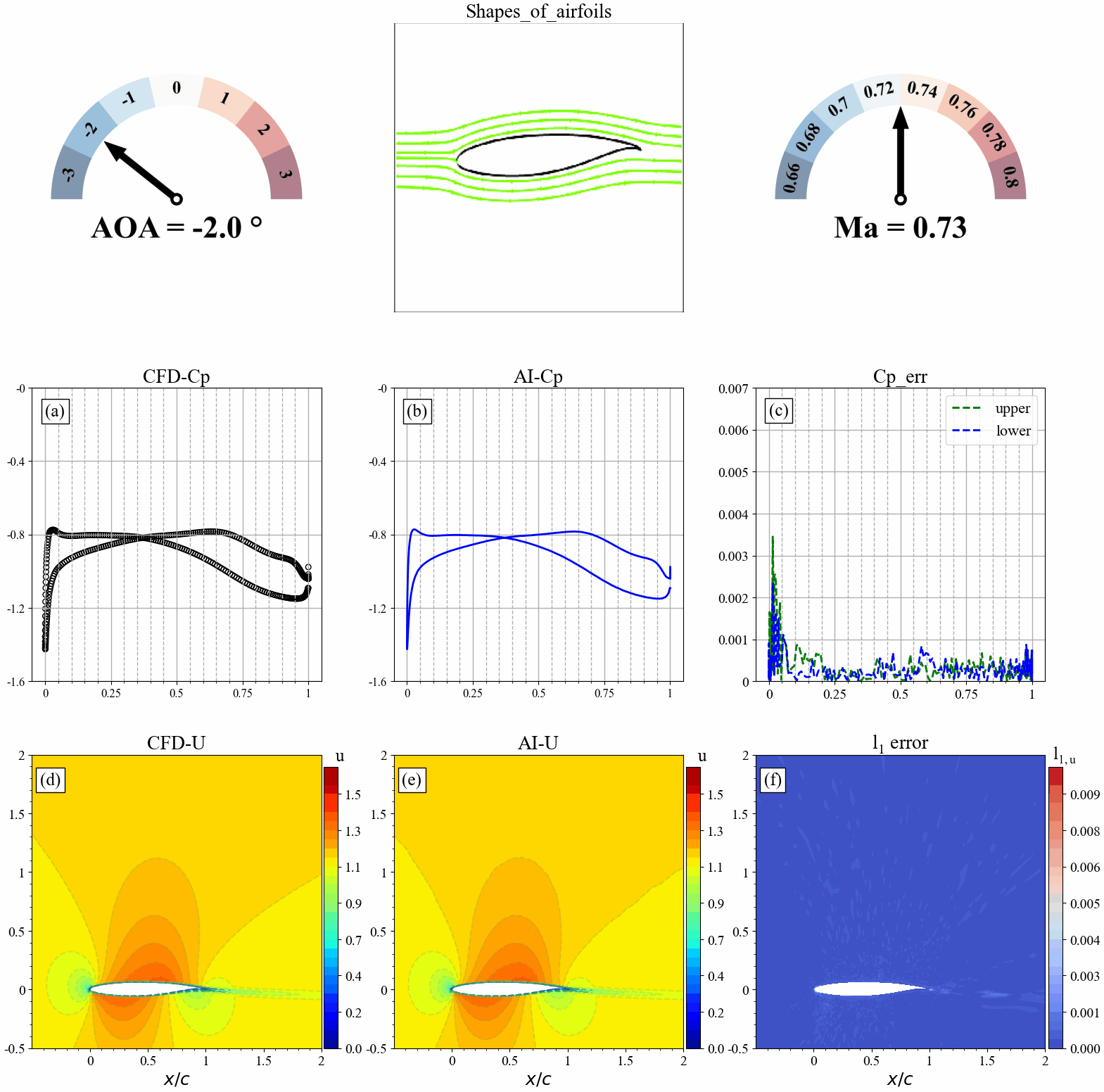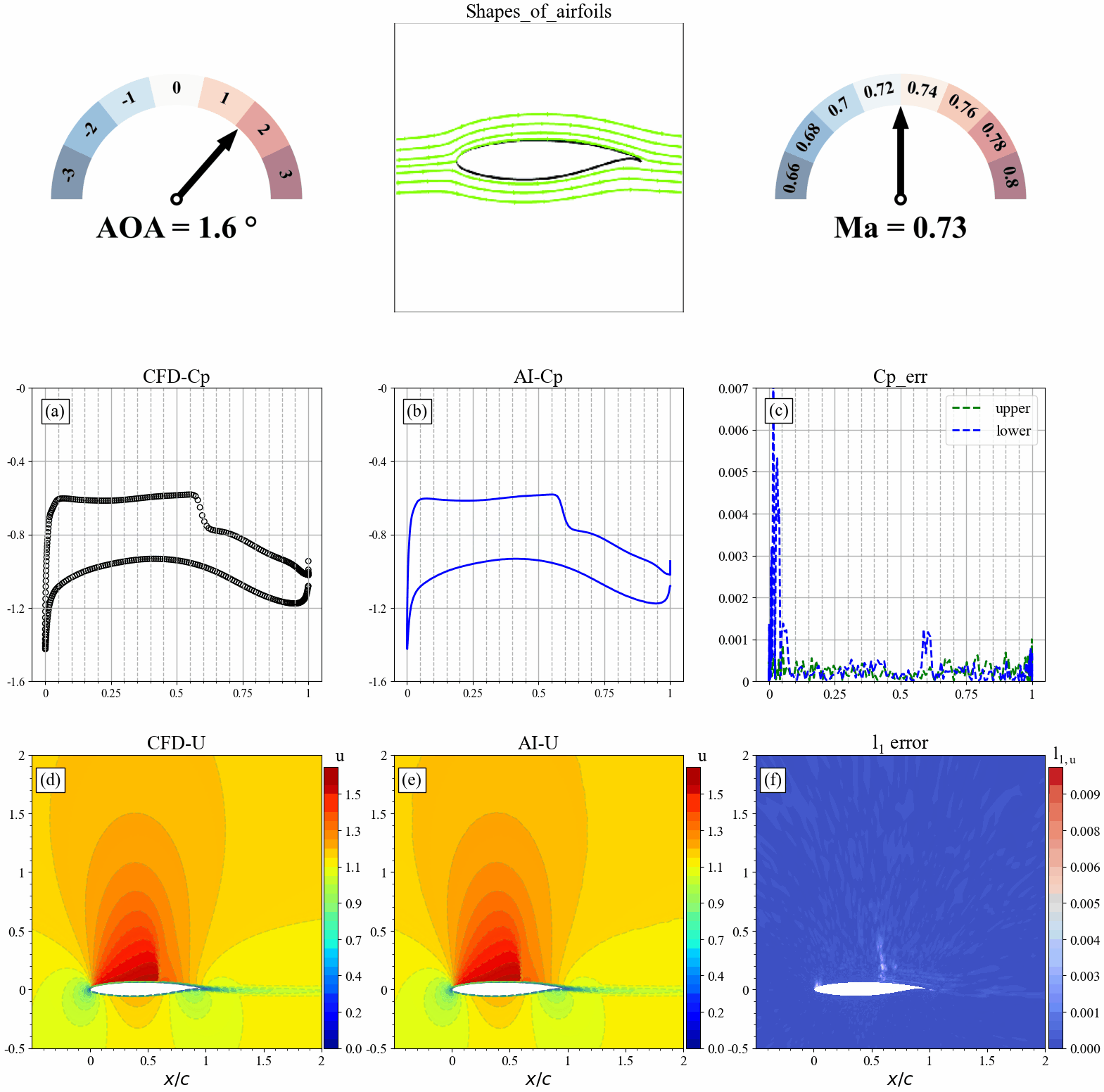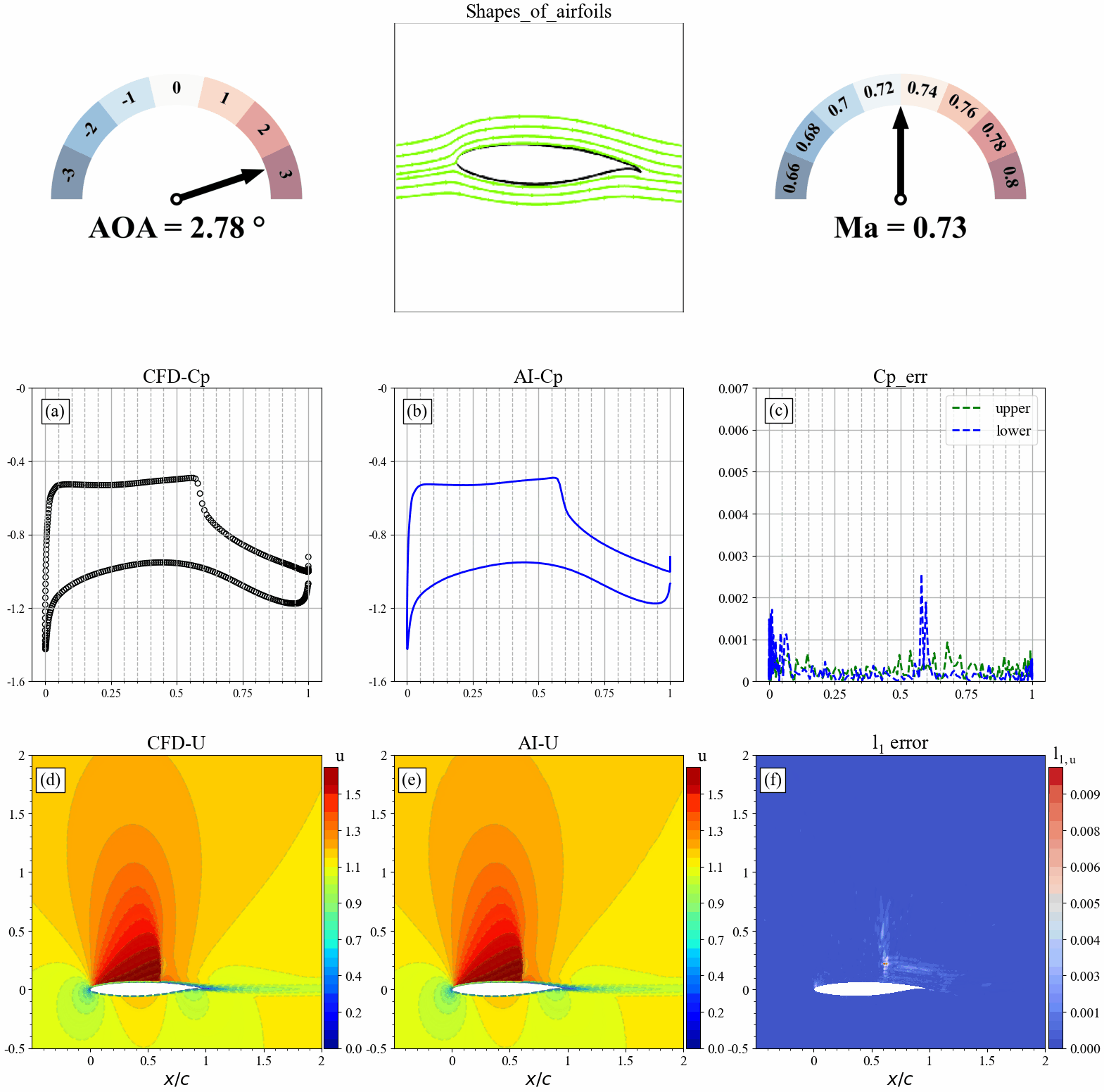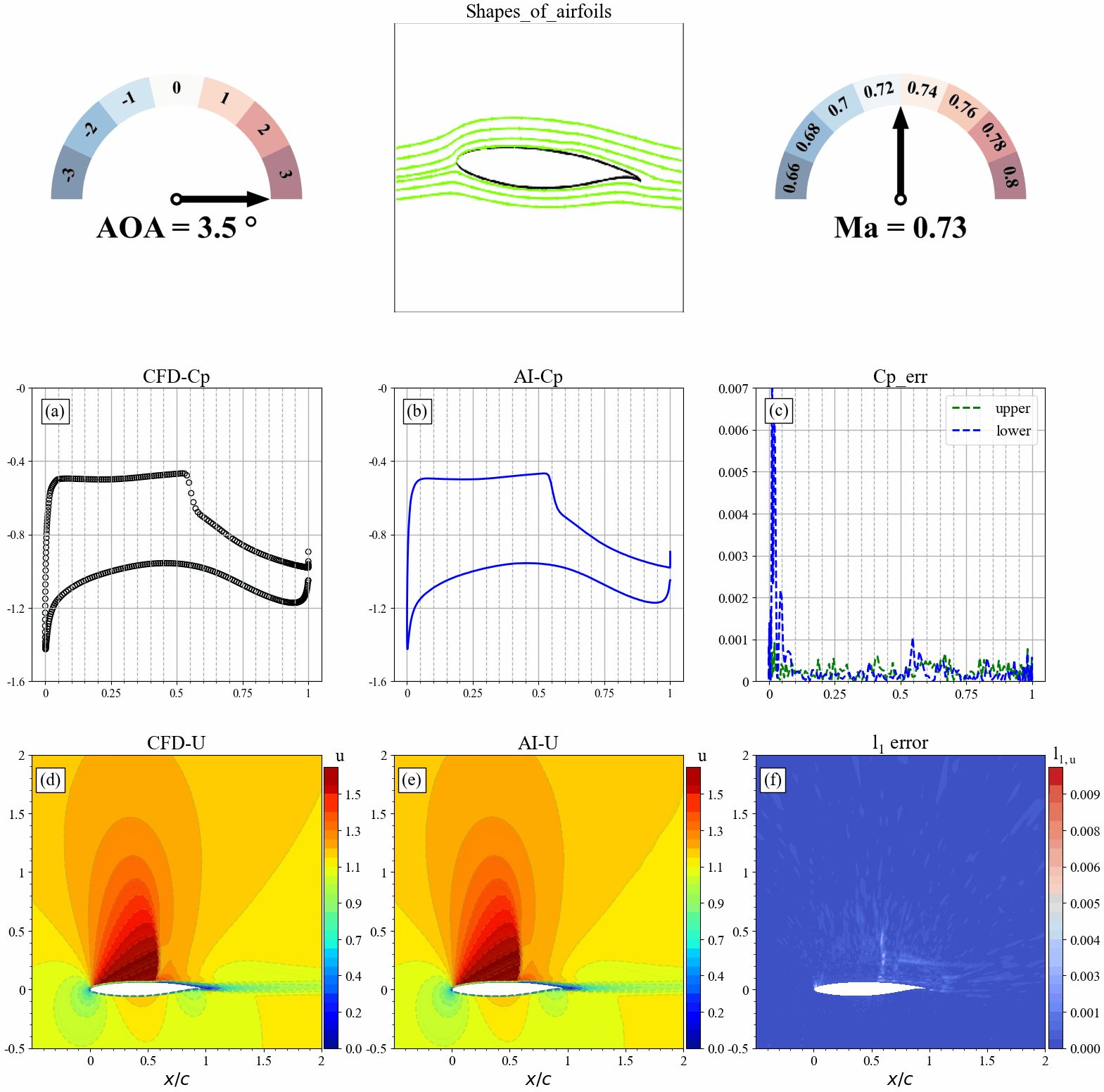
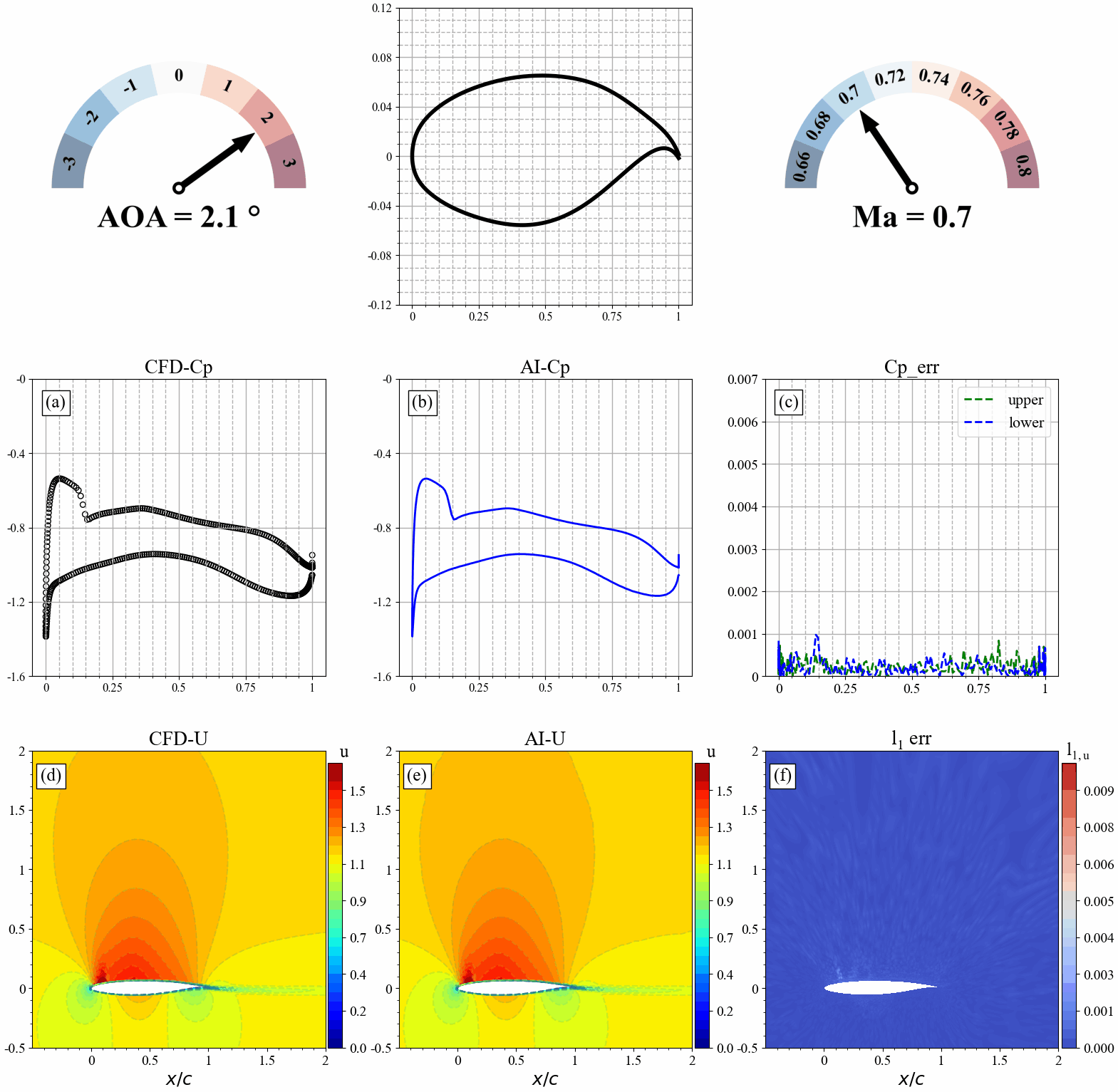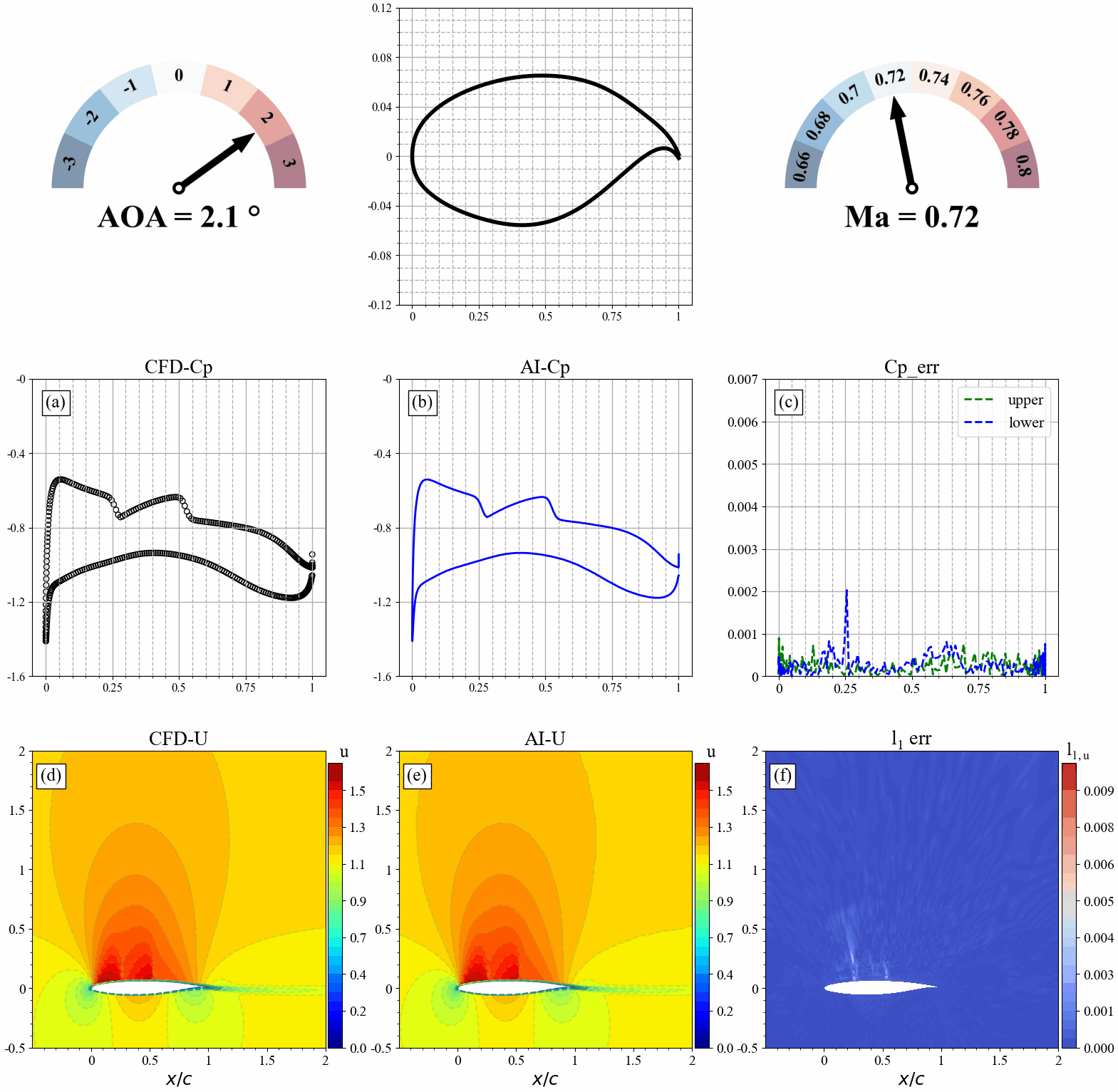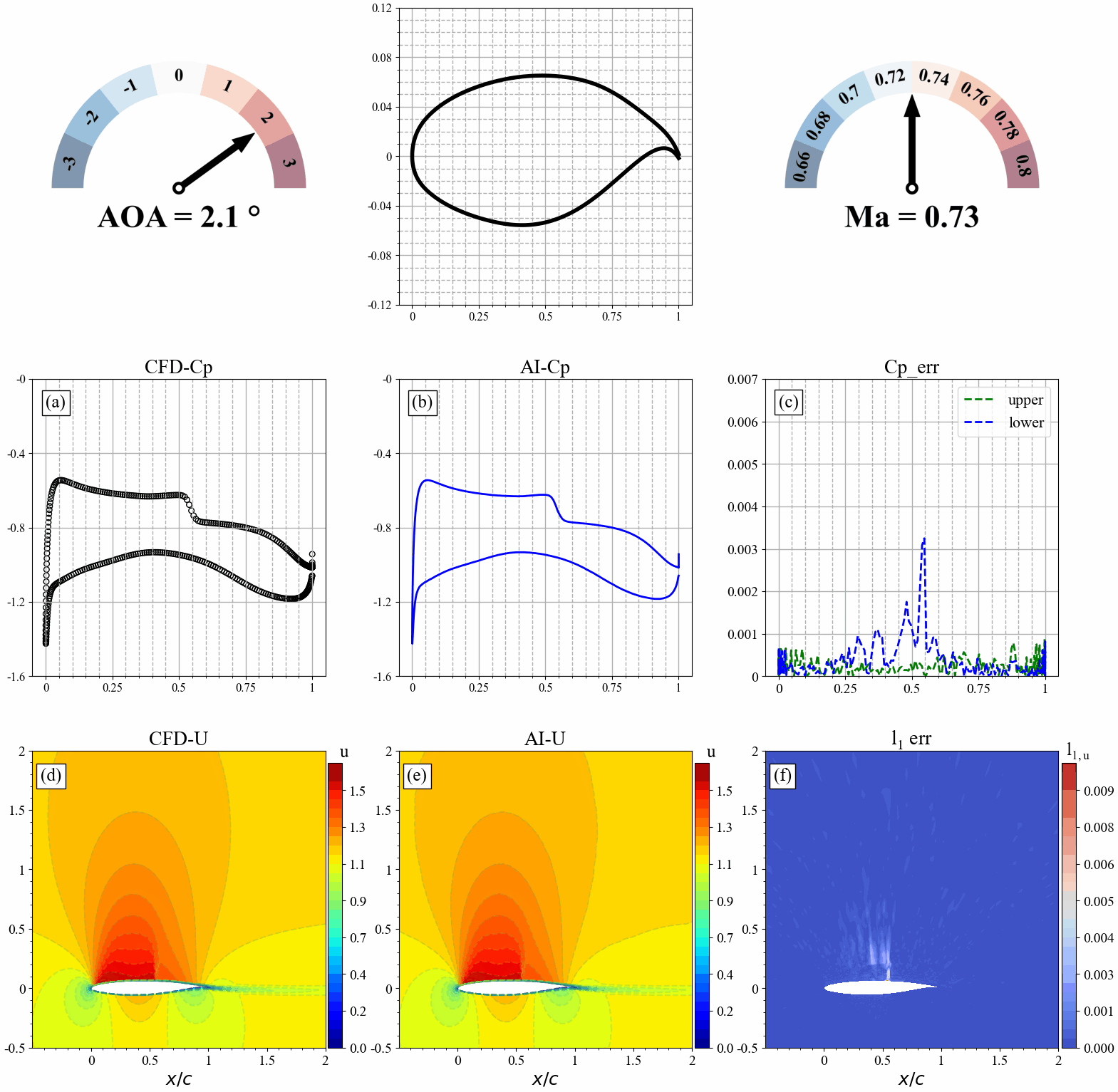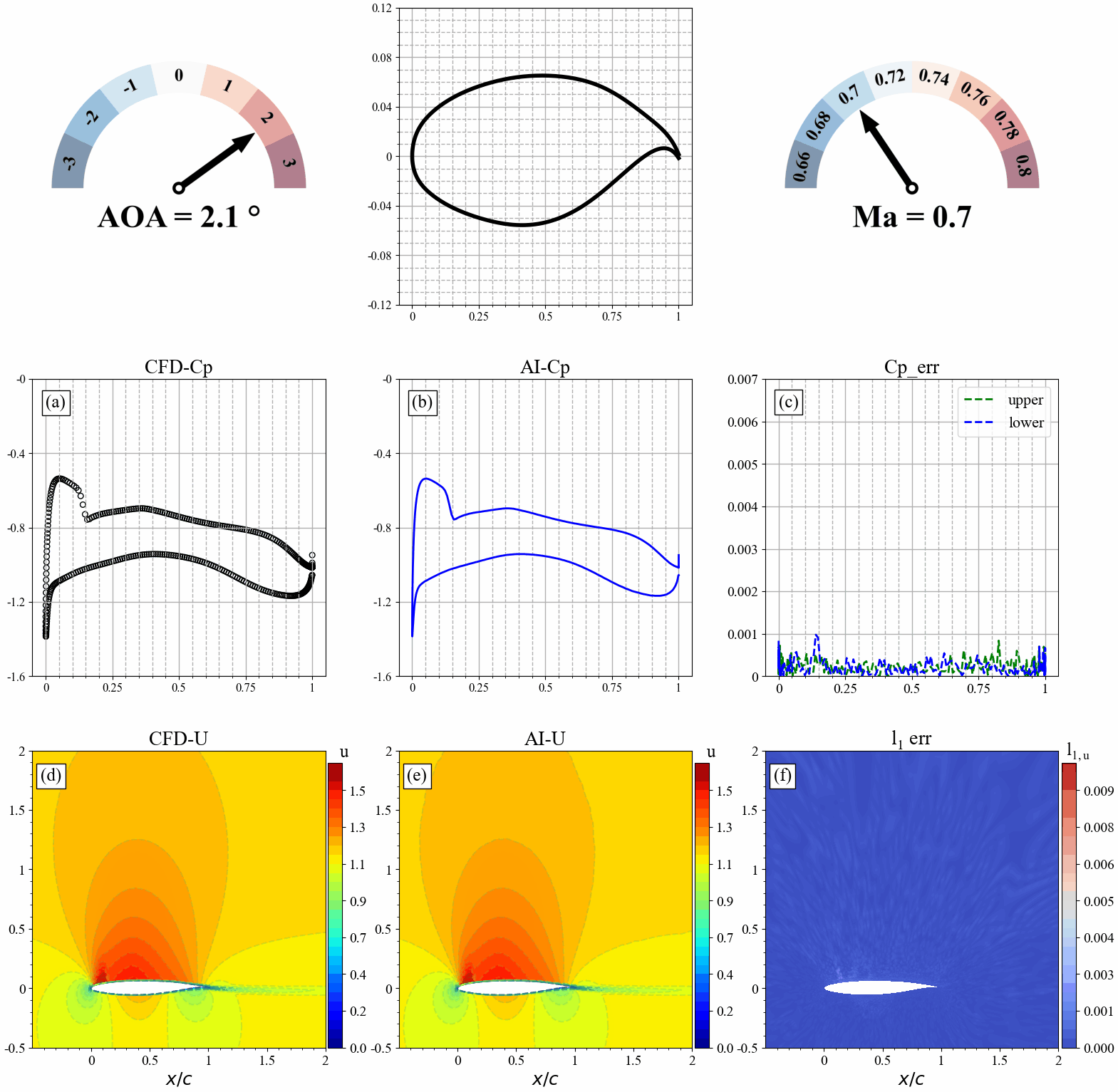
来流马赫数发生改变时，AI和CFD预测的表面压力分布，流场分布及其误差统计如下：

模型推理

模型训练结束后即可通过调用train.py中的train函数，train_mode设置为eval可进行推理，设置为finetune可进行迁移学习。

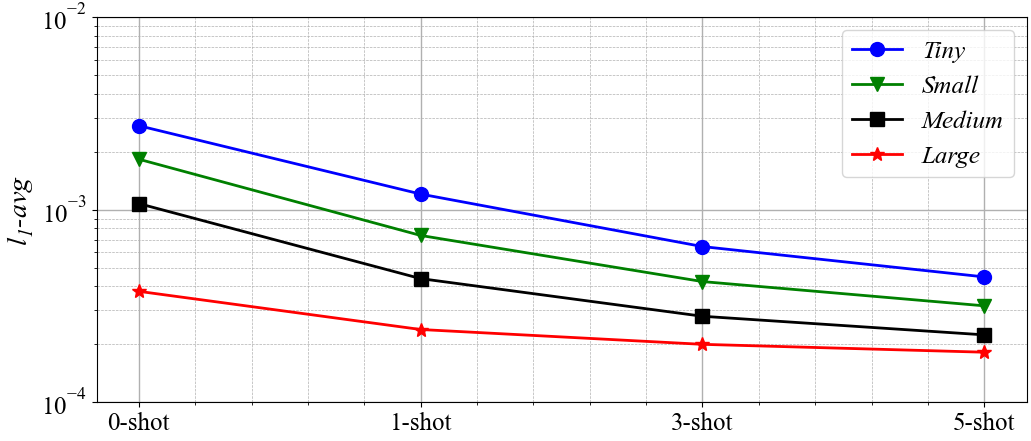
在设计新翼型时，需要考虑各种不同的初始边界条件（如不同的攻角或马赫数等），以进行气动性能的评估。为了提高模型的可推广性，从而提高其在工程场景中的效用，我们可以采用迁移学习的方式。具体做法为：先在大规模数据集预训练模型，最终在小数据集上进行快速的微调，从而实现模型对新工况的推理泛化。考虑到精度和时间消耗之间的权衡，我们一共考虑了四种不同大小的数据集去获取不同的预训练模型。与在较小数据集上进行预训练所需耗时较少，但预测精度较低；而在较大数据集上预训练，能够产生更准确的结果，但需要更多的预训练时间。

迁移学习的结果见下图。当使用微小数据集预训练模型时，至少需要三个新的流场才能实现4e-4的精度。相反，当使用小、中或大数据集预训练模型时，只需要一个新的流场，并且可以保持1e-4的精度。此外，通过使用5个流场的迁移学习，\(l_{1\_avg}\)可以至少减少50%。使用大数据集预训练的模型可以在zero-shot的情况下以较高的精度预测流场。使用不同规模和不同大小的数据集获得的微调结果如下图所示。微调所需的时间远低于生成样本所需的时间，当微调结束后，即可对新翼型的其他工况进行快速推理。因此，基于迁移学习的微调技术在工程应用中极具价值。