基于MindSpore Flow求解PINNs问题
概述
本教程基于二维Poisson问题介绍使用sympy定义第一类边界条件(Dirichlet boundary condition)和第二类边界条件(Neumann boundary condition),并训练一个物理信息神经网络模型。本教程主要介绍如下三个方面:
如何基于MindSpore Flow使用sympy便捷定义偏微分方程;
如何在模型中定义第一类边界条件和第二类边界条件;
如何利用MindSpore函数式编程范式训练一个物理信息神经网络。
问题描述
泊松方程是一个在理论物理中具有广泛效用的椭圆偏微分方程。例如,泊松方程的解是由给定电荷或质量密度分布引起的势场;在已知势场的情况下,可以计算静电或引力(力)场。 我们从二维齐次泊松方程出发,
其中 u 是主变量, f 是源项, \(\Delta\) 表示拉普拉斯运算符。
我们考虑源项 f为常数 (\(f=1.0\))则泊松方程可以表示为:
本案例中,使用Dirichlet边界条件和Neumann边界条件。格式如下:
外圆边界上的Dirichlet边界条件:
内圆边界上的Neumann边界条件:
本案例利用PINNs方法学习 \((x, y) \mapsto u\),实现泊松方程的求解。
技术路径
MindSpore Flow求解该问题的具体流程如下:
创建数据集。
构建模型。
优化器。
Poisson2D。
模型训练。
模型推理及可视化。
导入依赖库
[1]:
import time
import matplotlib.pyplot as plt
import numpy as np
import sympy
from sympy import symbols, Function, diff
import mindspore as ms
from mindspore import nn, ops, Tensor, set_context, set_seed, jit
from mindspore import dtype as mstype
set_seed(123456)
set_context(mode=ms.GRAPH_MODE, device_target="GPU", device_id=0)
创建数据集
本案例根据求解域、边值条件进行随机采样,使用Disk和CSGXOR几何模块构建输入输出边界和作用域,生成训练数据集与测试数据集。Disk和CSGXOR由MindSpore Flow的geometry模块导入。下载数据生成的Python文件。
[2]:
from mindflow.geometry import generate_sampling_config, Disk, CSGXOR
class MyIterable:
def __init__(self, domain, bc_outer, bc_inner, bc_inner_normal):
self._index = 0
self._domain = domain.astype(np.float32)
self._bc_outer = bc_outer.astype(np.float32)
self._bc_inner = bc_inner.astype(np.float32)
self._bc_inner_normal = bc_inner_normal.astype(np.float32)
def __next__(self):
if self._index >= len(self._domain):
raise StopIteration
item = (self._domain[self._index], self._bc_outer[self._index], self._bc_inner[self._index],
self._bc_inner_normal[self._index])
self._index += 1
return item
def __iter__(self):
self._index = 0
return self
def __len__(self):
return len(self._domain)
def _get_region(config):
indisk_cfg = config["in_disk"]
in_disk = Disk(indisk_cfg["name"], (indisk_cfg["center_x"], indisk_cfg["center_y"]), indisk_cfg["radius"])
outdisk_cfg = config["out_disk"]
out_disk = Disk(outdisk_cfg["name"], (outdisk_cfg["center_x"], outdisk_cfg["center_y"]), outdisk_cfg["radius"])
union = CSGXOR(out_disk, in_disk)
return in_disk, out_disk, union
def create_training_dataset(config):
'''create_training_dataset'''
in_disk, out_disk, union = _get_region(config)
union.set_sampling_config(generate_sampling_config(config["data"]))
domain = union.sampling(geom_type="domain")
out_disk.set_sampling_config(generate_sampling_config(config["data"]))
bc_outer, _ = out_disk.sampling(geom_type="BC")
in_disk.set_sampling_config(generate_sampling_config(config["data"]))
bc_inner, bc_inner_normal = in_disk.sampling(geom_type="BC")
plt.figure()
plt.axis("equal")
plt.scatter(domain[:, 0], domain[:, 1], c="powderblue", s=0.5)
plt.scatter(bc_outer[:, 0], bc_outer[:, 1], c="darkorange", s=0.005)
plt.scatter(bc_inner[:, 0], bc_inner[:, 1], c="cyan", s=0.005)
plt.show()
dataset = ms.dataset.GeneratorDataset(source=MyIterable(domain, bc_outer, bc_inner, (-1.0) * bc_inner_normal),
column_names=["data", "bc_outer", "bc_inner", "bc_inner_normal"])
return dataset
def _numerical_solution(x, y):
return (4.0 - x ** 2 - y ** 2) / 4
def create_test_dataset(config):
"""create test dataset"""
_, _, union = _get_region(config)
union.set_sampling_config(generate_sampling_config(config["data"]))
test_data = union.sampling(geom_type="domain")
test_label = _numerical_solution(test_data[:, 0], test_data[:, 1]).reshape(-1, 1)
return test_data, test_label
数据生成的几何形状为一个圆环,内圆半径为1.0,外圆半径为2.0,边界和域内数据量大小均为8192。具体生成参数设置如下:
[3]:
in_disk = {"name": "in_disk", "center_x": 0.0, "center_y": 0.0, "radius": 1.0}
out_disk = {"name": "out_disk", "center_x": 0.0, "center_y": 0.0, "radius": 2.0}
domain = {"size": 8192, "random_sampling": True, "sampler": "uniform"}
BC = {"size": 8192, "random_sampling": True, "sampler": "uniform", "with_normal": True}
data = {"domain": domain, "BC": BC}
config = {"in_disk": in_disk, "out_disk": out_disk, "data": data}
# create training dataset
dataset = create_training_dataset(config)
train_dataset = dataset.batch(batch_size=8192)
# create test dataset
inputs, label = create_test_dataset(config)

构建模型
本例使用MultiScaleFCCell构建网络模型。MultiScaleFCCell网络由MindSpore Flow的cell模块导入。所构建的全连接网络,深度为6层,激活函数为tanh函数。
[4]:
from mindflow.cell import MultiScaleFCCell
model = MultiScaleFCCell(in_channels=2,
out_channels=1,
layers=6,
neurons=128,
residual=False,
act="tanh",
num_scales=1)
优化器
优化器使用Adaptive Moment Estimation (Adam)。
[5]:
optimizer = nn.Adam(model.trainable_params(), 0.001)
Poisson2D
Poisson2D包含求解问题的控制方程、狄利克雷边界条件、诺曼边界条件等。使用sympy以符号形式定义偏微分方程并求解所有方程的损失值。
符号声明
定义x、 y、 n分别表示横坐标、纵坐标和内圆边界的法向量。输出u为关于x和 y的函数。
[6]:
x, y, n = symbols('x y n')
u = Function('u')(x, y)
# independent variables
in_vars = [x, y]
print("independent variables: ", in_vars)
# dependent variables
out_vars = [u]
print("dependent variables: ", out_vars)
independent variables: [x, y]
dependent variables: [u(x, y)]
控制方程
[7]:
govern_eq = diff(u, (x, 2)) + diff(u, (y, 2)) + 1.0
print("governing equation: ", govern_eq)
governing equation: Derivative(u(x, y), (x, 2)) + Derivative(u(x, y), (y, 2)) + 1.0
Dirichlet边界条件
[8]:
bc_outer = u
print("bc_outer equation: ", bc_outer)
bc_outer equation: u(x, y)
Neumann边界条件
[9]:
bc_inner = sympy.Derivative(u, n) - 0.5
print("bc_inner equation: ", bc_inner)
bc_inner equation: Derivative(u(x, y), n) - 0.5
基于Poisson基类结合上面定义的控制方程和边界条件,定义下述Poisson2D问题。Poisson基类由MindSpore Flow的pde模块导入。下载Poisson2D问题的Python文件。
[10]:
from mindflow.pde import Poisson, sympy_to_mindspore
class Poisson2D(Poisson):
def __init__(self, model, loss_fn="mse"):
super(Poisson2D, self).__init__(model, loss_fn=loss_fn)
self.bc_outer_nodes = sympy_to_mindspore(self.bc_outer(), self.in_vars, self.out_vars)
self.bc_inner_nodes = sympy_to_mindspore(self.bc_inner(), self.in_vars, self.out_vars)
def bc_outer(self):
bc_outer_eq = self.u
equations = {"bc_outer": bc_outer_eq}
return equations
def bc_inner(self):
bc_inner_eq = sympy.Derivative(self.u, self.normal) - 0.5
equations = {"bc_inner": bc_inner_eq}
return equations
def get_loss(self, pde_data, bc_outer_data, bc_inner_data, bc_inner_normal):
pde_res = self.parse_node(self.pde_nodes, inputs=pde_data)
pde_loss = self.loss_fn(pde_res[0], Tensor(np.array([0.0]), mstype.float32))
bc_inner_res = self.parse_node(self.bc_inner_nodes, inputs=bc_inner_data, norm=bc_inner_normal)
bc_inner_loss = self.loss_fn(bc_inner_res[0], Tensor(np.array([0.0]), mstype.float32))
bc_outer_res = self.parse_node(self.bc_outer_nodes, inputs=bc_outer_data)
bc_outer_loss = self.loss_fn(bc_outer_res[0], Tensor(np.array([0.0]), mstype.float32))
return pde_loss + bc_inner_loss + bc_outer_loss
problem = Poisson2D(model)
poisson: Derivative(u(x, y), (x, 2)) + Derivative(u(x, y), (y, 2)) + 1.0
Item numbers of current derivative formula nodes: 3
bc_outer: u(x, y)
Item numbers of current derivative formula nodes: 1
bc_inner: Derivative(u(x, y), n) - 0.5
Item numbers of current derivative formula nodes: 2
模型训练
使用MindSpore >= 2.0.0的版本,采用函数式编程的方式训练网络。下载训练的Python文件。
[11]:
# define forward function
def forward_fn(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal):
loss = problem.get_loss(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal)
return loss
# define grad function
grad_fn = ms.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=False)
# using jit to accelerate training
@jit
def train_step(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal):
loss, grads = grad_fn(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal)
loss = ops.depend(loss, optimizer(grads))
return loss
下载训练过程计算损失的Python文件。
[12]:
def _calculate_error(label, prediction):
'''calculate l2-error to evaluate accuracy'''
error = label - prediction
l2_error = np.sqrt(np.sum(np.square(error[..., 0]))) / np.sqrt(np.sum(np.square(label[..., 0])))
return l2_error
def _get_prediction(model, inputs, label_shape, batch_size):
'''calculate the prediction respect to the given inputs'''
prediction = np.zeros(label_shape)
prediction = prediction.reshape((-1, label_shape[1]))
inputs = inputs.reshape((-1, inputs.shape[1]))
time_beg = time.time()
index = 0
while index < inputs.shape[0]:
index_end = min(index + batch_size, inputs.shape[0])
test_batch = Tensor(inputs[index: index_end, :], mstype.float32)
prediction[index: index_end, :] = model(test_batch).asnumpy()
index = index_end
print(" predict total time: {} ms".format((time.time() - time_beg) * 1000))
prediction = prediction.reshape(label_shape)
prediction = prediction.reshape((-1, label_shape[1]))
return prediction
def calculate_l2_error(model, inputs, label, batch_size):
label_shape = label.shape
prediction = _get_prediction(model, inputs, label_shape, batch_size)
label = label.reshape((-1, label_shape[1]))
l2_error = _calculate_error(label, prediction)
print(" l2_error: ", l2_error)
print("==================================================================================================")
[13]:
epochs = 5000
steps_per_epochs = train_dataset.get_dataset_size()
sink_process = ms.data_sink(train_step, train_dataset, sink_size=1)
for epoch in range(1, epochs + 1):
# train
time_beg = time.time()
model.set_train(True)
for _ in range(steps_per_epochs):
step_train_loss = sink_process()
print(f"epoch: {epoch} train loss: {step_train_loss} epoch time: {(time.time() - time_beg)*1000 :.3f} ms")
model.set_train(False)
if epoch % 100 == 0:
# eval
calculate_l2_error(model, inputs, label, 8192)
epoch: 1 train loss: 1.2577767 epoch time: 6024.162 ms
epoch: 2 train loss: 1.2554792 epoch time: 70.884 ms
epoch: 3 train loss: 1.2534575 epoch time: 71.048 ms
epoch: 4 train loss: 1.2516733 epoch time: 100.632 ms
epoch: 5 train loss: 1.2503157 epoch time: 65.656 ms
epoch: 6 train loss: 1.2501826 epoch time: 137.487 ms
epoch: 7 train loss: 1.2511331 epoch time: 51.191 ms
epoch: 8 train loss: 1.2508672 epoch time: 65.980 ms
epoch: 9 train loss: 1.2503275 epoch time: 211.144 ms
epoch: 10 train loss: 1.2500556 epoch time: 224.515 ms
epoch: 11 train loss: 1.2500004 epoch time: 225.964 ms
epoch: 12 train loss: 1.2500298 epoch time: 220.117 ms
epoch: 13 train loss: 1.2500703 epoch time: 221.441 ms
epoch: 14 train loss: 1.2500948 epoch time: 220.214 ms
epoch: 15 train loss: 1.2500978 epoch time: 219.836 ms
epoch: 16 train loss: 1.250083 epoch time: 220.141 ms
epoch: 17 train loss: 1.2500567 epoch time: 229.682 ms
epoch: 18 train loss: 1.2500263 epoch time: 216.013 ms
epoch: 19 train loss: 1.2500005 epoch time: 218.639 ms
epoch: 20 train loss: 1.2499874 epoch time: 228.765 ms
epoch: 21 train loss: 1.2499917 epoch time: 230.179 ms
epoch: 22 train loss: 1.250007 epoch time: 215.476 ms
epoch: 23 train loss: 1.250018 epoch time: 224.334 ms
epoch: 24 train loss: 1.2500123 epoch time: 217.322 ms
epoch: 25 train loss: 1.249995 epoch time: 217.106 ms
epoch: 26 train loss: 1.249982 epoch time: 217.612 ms
epoch: 27 train loss: 1.249983 epoch time: 223.639 ms
epoch: 28 train loss: 1.2499921 epoch time: 226.419 ms
epoch: 29 train loss: 1.2499963 epoch time: 212.248 ms
epoch: 30 train loss: 1.2499878 epoch time: 225.295 ms
epoch: 31 train loss: 1.2499707 epoch time: 219.656 ms
epoch: 32 train loss: 1.2499548 epoch time: 218.019 ms
epoch: 33 train loss: 1.2499464 epoch time: 226.645 ms
epoch: 34 train loss: 1.2499409 epoch time: 222.399 ms
epoch: 35 train loss: 1.249928 epoch time: 224.290 ms
epoch: 36 train loss: 1.2499026 epoch time: 221.664 ms
epoch: 37 train loss: 1.2498704 epoch time: 221.300 ms
epoch: 38 train loss: 1.2498367 epoch time: 220.392 ms
epoch: 39 train loss: 1.2497979 epoch time: 221.848 ms
epoch: 40 train loss: 1.2497431 epoch time: 219.831 ms
epoch: 41 train loss: 1.2496608 epoch time: 217.333 ms
epoch: 42 train loss: 1.249544 epoch time: 220.116 ms
epoch: 43 train loss: 1.2493837 epoch time: 214.985 ms
epoch: 44 train loss: 1.2491598 epoch time: 220.717 ms
epoch: 45 train loss: 1.248828 epoch time: 216.047 ms
epoch: 46 train loss: 1.2483226 epoch time: 218.554 ms
epoch: 47 train loss: 1.247554 epoch time: 221.158 ms
epoch: 48 train loss: 1.2463655 epoch time: 218.594 ms
epoch: 49 train loss: 1.2444699 epoch time: 216.152 ms
epoch: 50 train loss: 1.2413855 epoch time: 220.306 ms
epoch: 51 train loss: 1.2362938 epoch time: 211.876 ms
epoch: 52 train loss: 1.2277732 epoch time: 213.732 ms
epoch: 53 train loss: 1.2135327 epoch time: 219.945 ms
epoch: 54 train loss: 1.1906419 epoch time: 217.820 ms
epoch: 55 train loss: 1.1573513 epoch time: 225.694 ms
epoch: 56 train loss: 1.1058999 epoch time: 221.004 ms
epoch: 57 train loss: 1.0343707 epoch time: 225.404 ms
epoch: 58 train loss: 0.9365865 epoch time: 224.163 ms
epoch: 59 train loss: 0.83171475 epoch time: 211.383 ms
epoch: 60 train loss: 0.77913564 epoch time: 229.284 ms
epoch: 61 train loss: 0.74204475 epoch time: 223.518 ms
epoch: 62 train loss: 0.80121577 epoch time: 229.029 ms
epoch: 63 train loss: 0.8549291 epoch time: 223.576 ms
epoch: 64 train loss: 0.7383551 epoch time: 235.727 ms
epoch: 65 train loss: 0.72710323 epoch time: 222.646 ms
epoch: 66 train loss: 0.6702794 epoch time: 226.154 ms
epoch: 67 train loss: 0.6987355 epoch time: 221.565 ms
epoch: 68 train loss: 0.6746455 epoch time: 234.406 ms
epoch: 69 train loss: 0.70462525 epoch time: 226.131 ms
epoch: 70 train loss: 0.67767555 epoch time: 229.177 ms
epoch: 71 train loss: 0.6821881 epoch time: 224.217 ms
epoch: 72 train loss: 0.64521456 epoch time: 223.717 ms
epoch: 73 train loss: 0.6368966 epoch time: 226.217 ms
epoch: 74 train loss: 0.592155 epoch time: 219.816 ms
epoch: 75 train loss: 0.6024764 epoch time: 214.097 ms
epoch: 76 train loss: 0.58170027 epoch time: 224.460 ms
epoch: 77 train loss: 0.5691892 epoch time: 223.964 ms
epoch: 78 train loss: 0.5925416 epoch time: 226.897 ms
epoch: 79 train loss: 0.61034954 epoch time: 221.710 ms
epoch: 80 train loss: 0.5831032 epoch time: 231.325 ms
epoch: 81 train loss: 0.5364084 epoch time: 222.517 ms
epoch: 82 train loss: 0.5502083 epoch time: 215.709 ms
epoch: 83 train loss: 0.5633007 epoch time: 209.054 ms
epoch: 84 train loss: 0.52546465 epoch time: 219.471 ms
epoch: 85 train loss: 0.53276706 epoch time: 218.961 ms
epoch: 86 train loss: 0.55396163 epoch time: 237.759 ms
epoch: 87 train loss: 0.5206229 epoch time: 219.588 ms
epoch: 88 train loss: 0.5106571 epoch time: 225.651 ms
epoch: 89 train loss: 0.53332406 epoch time: 224.282 ms
epoch: 90 train loss: 0.53076947 epoch time: 235.400 ms
epoch: 91 train loss: 0.5049336 epoch time: 215.371 ms
epoch: 92 train loss: 0.48215953 epoch time: 239.344 ms
epoch: 93 train loss: 0.4843874 epoch time: 218.674 ms
epoch: 94 train loss: 0.51292086 epoch time: 221.709 ms
epoch: 95 train loss: 0.56979203 epoch time: 225.018 ms
epoch: 96 train loss: 0.61994594 epoch time: 219.800 ms
epoch: 97 train loss: 0.4962491 epoch time: 223.785 ms
epoch: 98 train loss: 0.4802659 epoch time: 230.708 ms
epoch: 99 train loss: 0.54967964 epoch time: 221.209 ms
epoch: 100 train loss: 0.46414006 epoch time: 223.953 ms
predict total time: 124.87483024597168 ms
l2_error: 0.9584533008207833
==================================================================================================
...
epoch: 4901 train loss: 0.00012433846 epoch time: 241.115 ms
epoch: 4902 train loss: 0.00012422525 epoch time: 239.142 ms
epoch: 4903 train loss: 0.00012412701 epoch time: 234.900 ms
epoch: 4904 train loss: 0.00012404467 epoch time: 237.946 ms
epoch: 4905 train loss: 0.000123965 epoch time: 236.818 ms
epoch: 4906 train loss: 0.0001238766 epoch time: 255.728 ms
epoch: 4907 train loss: 0.00012378026 epoch time: 225.175 ms
epoch: 4908 train loss: 0.00012368544 epoch time: 241.107 ms
epoch: 4909 train loss: 0.00012359957 epoch time: 248.310 ms
epoch: 4910 train loss: 0.00012352059 epoch time: 239.238 ms
epoch: 4911 train loss: 0.0001234413 epoch time: 229.464 ms
epoch: 4912 train loss: 0.00012335769 epoch time: 228.504 ms
epoch: 4913 train loss: 0.00012327175 epoch time: 238.126 ms
epoch: 4914 train loss: 0.00012318943 epoch time: 236.290 ms
epoch: 4915 train loss: 0.00012311469 epoch time: 221.079 ms
epoch: 4916 train loss: 0.00012304715 epoch time: 238.825 ms
epoch: 4917 train loss: 0.00012298509 epoch time: 243.784 ms
epoch: 4918 train loss: 0.00012292914 epoch time: 235.416 ms
epoch: 4919 train loss: 0.00012288446 epoch time: 221.510 ms
epoch: 4920 train loss: 0.00012286083 epoch time: 244.597 ms
epoch: 4921 train loss: 0.00012286832 epoch time: 245.989 ms
epoch: 4922 train loss: 0.00012292268 epoch time: 234.209 ms
epoch: 4923 train loss: 0.00012304373 epoch time: 223.089 ms
epoch: 4924 train loss: 0.0001232689 epoch time: 234.764 ms
epoch: 4925 train loss: 0.00012365196 epoch time: 246.427 ms
epoch: 4926 train loss: 0.00012429312 epoch time: 233.304 ms
epoch: 4927 train loss: 0.0001253246 epoch time: 221.859 ms
epoch: 4928 train loss: 0.00012700919 epoch time: 230.224 ms
epoch: 4929 train loss: 0.00012967733 epoch time: 254.334 ms
epoch: 4930 train loss: 0.000134056 epoch time: 242.256 ms
epoch: 4931 train loss: 0.00014098533 epoch time: 225.075 ms
epoch: 4932 train loss: 0.00015257315 epoch time: 235.392 ms
epoch: 4933 train loss: 0.00017092828 epoch time: 243.934 ms
epoch: 4934 train loss: 0.00020245541 epoch time: 244.327 ms
epoch: 4935 train loss: 0.00025212576 epoch time: 238.360 ms
epoch: 4936 train loss: 0.00034049098 epoch time: 233.573 ms
epoch: 4937 train loss: 0.0004768648 epoch time: 242.150 ms
epoch: 4938 train loss: 0.0007306886 epoch time: 247.166 ms
epoch: 4939 train loss: 0.0011023732 epoch time: 242.486 ms
epoch: 4940 train loss: 0.001834287 epoch time: 237.257 ms
epoch: 4941 train loss: 0.0027812878 epoch time: 242.192 ms
epoch: 4942 train loss: 0.004766387 epoch time: 236.694 ms
epoch: 4943 train loss: 0.006648433 epoch time: 223.730 ms
epoch: 4944 train loss: 0.010807082 epoch time: 237.647 ms
epoch: 4945 train loss: 0.01206318 epoch time: 233.036 ms
epoch: 4946 train loss: 0.015489452 epoch time: 227.594 ms
epoch: 4947 train loss: 0.011565584 epoch time: 227.099 ms
epoch: 4948 train loss: 0.008471975 epoch time: 231.612 ms
epoch: 4949 train loss: 0.0035123175 epoch time: 276.854 ms
epoch: 4950 train loss: 0.00091841083 epoch time: 229.893 ms
epoch: 4951 train loss: 0.00053060305 epoch time: 231.533 ms
epoch: 4952 train loss: 0.0017638807 epoch time: 231.814 ms
epoch: 4953 train loss: 0.0035763814 epoch time: 236.456 ms
epoch: 4954 train loss: 0.004056363 epoch time: 244.743 ms
epoch: 4955 train loss: 0.0039708405 epoch time: 221.469 ms
epoch: 4956 train loss: 0.0027319128 epoch time: 236.732 ms
epoch: 4957 train loss: 0.0017904624 epoch time: 231.612 ms
epoch: 4958 train loss: 0.0009970744 epoch time: 244.820 ms
epoch: 4959 train loss: 0.00061692565 epoch time: 221.442 ms
epoch: 4960 train loss: 0.0007383662 epoch time: 245.430 ms
epoch: 4961 train loss: 0.0012403185 epoch time: 231.007 ms
epoch: 4962 train loss: 0.0018439001 epoch time: 233.718 ms
epoch: 4963 train loss: 0.0017326038 epoch time: 224.514 ms
epoch: 4964 train loss: 0.0011022249 epoch time: 237.367 ms
epoch: 4965 train loss: 0.00033718432 epoch time: 242.038 ms
epoch: 4966 train loss: 0.00018465787 epoch time: 230.688 ms
epoch: 4967 train loss: 0.00055812683 epoch time: 218.956 ms
epoch: 4968 train loss: 0.00085373345 epoch time: 239.294 ms
epoch: 4969 train loss: 0.0007744754 epoch time: 234.656 ms
epoch: 4970 train loss: 0.00047988302 epoch time: 243.434 ms
epoch: 4971 train loss: 0.0003720247 epoch time: 214.474 ms
epoch: 4972 train loss: 0.0004015266 epoch time: 239.108 ms
epoch: 4973 train loss: 0.00037753512 epoch time: 246.952 ms
epoch: 4974 train loss: 0.0002867286 epoch time: 235.668 ms
epoch: 4975 train loss: 0.00029258506 epoch time: 229.418 ms
epoch: 4976 train loss: 0.00041505875 epoch time: 239.248 ms
epoch: 4977 train loss: 0.00043451862 epoch time: 235.341 ms
epoch: 4978 train loss: 0.00030042438 epoch time: 236.248 ms
epoch: 4979 train loss: 0.00015146247 epoch time: 218.208 ms
epoch: 4980 train loss: 0.00016080803 epoch time: 246.693 ms
epoch: 4981 train loss: 0.00027215388 epoch time: 238.106 ms
epoch: 4982 train loss: 0.00031257677 epoch time: 236.889 ms
epoch: 4983 train loss: 0.0002639915 epoch time: 222.054 ms
epoch: 4984 train loss: 0.000204898 epoch time: 231.757 ms
epoch: 4985 train loss: 0.00019457101 epoch time: 246.356 ms
epoch: 4986 train loss: 0.00018954299 epoch time: 247.128 ms
epoch: 4987 train loss: 0.00016800698 epoch time: 219.524 ms
epoch: 4988 train loss: 0.00016529267 epoch time: 240.068 ms
epoch: 4989 train loss: 0.00019697993 epoch time: 235.206 ms
epoch: 4990 train loss: 0.00021988692 epoch time: 237.431 ms
epoch: 4991 train loss: 0.00019355604 epoch time: 219.045 ms
epoch: 4992 train loss: 0.00014973793 epoch time: 246.853 ms
epoch: 4993 train loss: 0.00013542885 epoch time: 226.068 ms
epoch: 4994 train loss: 0.00015176873 epoch time: 248.399 ms
epoch: 4995 train loss: 0.0001647438 epoch time: 217.880 ms
epoch: 4996 train loss: 0.00016070419 epoch time: 237.407 ms
epoch: 4997 train loss: 0.00015653059 epoch time: 235.727 ms
epoch: 4998 train loss: 0.00015907965 epoch time: 247.844 ms
epoch: 4999 train loss: 0.00015674165 epoch time: 226.864 ms
epoch: 5000 train loss: 0.00014248541 epoch time: 244.331 ms
predict total time: 1.7328262329101562 ms
l2_error: 0.00915682980750216
==================================================================================================
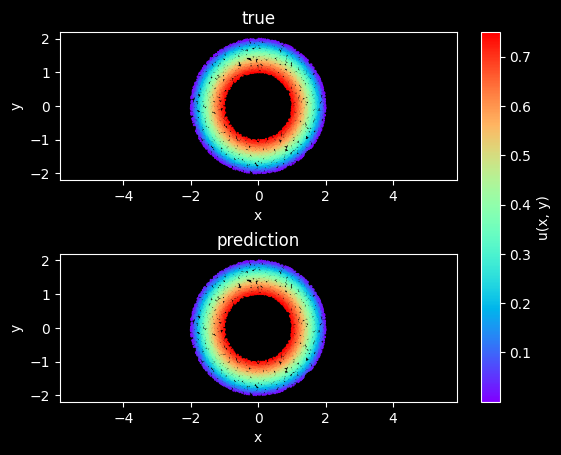
模型推理及可视化
训练后可对流场内所有数据点进行推理,并可视化相关结果。下载可视化结果的Python文件。
[14]:
def visual(model, inputs, label, epochs=1):
'''visual result for poisson 2D'''
fig, ax = plt.subplots(2, 1)
ax = ax.flatten()
plt.subplots_adjust(hspace=0.5)
ax0 = ax[0].scatter(inputs[:, 0], inputs[:, 1], c=label[:, 0], cmap=plt.cm.rainbow, s=0.5)
ax[0].set_title("true")
ax[0].set_xlabel('x')
ax[0].set_ylabel('y')
ax[0].axis('equal')
ax[1].scatter(inputs[:, 0], inputs[:, 1], c=model(Tensor(inputs, mstype.float32)), cmap=plt.cm.rainbow, s=0.5)
ax[1].set_title("prediction")
ax[1].set_xlabel('x')
ax[1].set_ylabel('y')
ax[1].axis('equal')
cbar = fig.colorbar(ax0, ax=[ax[0], ax[1]])
cbar.set_label('u(x, y)')
plt.savefig(f"images/{epochs}-result.jpg", dpi=600)
[15]:
# visualization
visual(model, inputs, label, 5000)