Solving PINNs Based on MindSpore Flow
Overview
This tutorial describes how to use sympy to define the Dirichlet boundary conditions and the Neumann boundary conditions based on the two-dimensional Poisson problem and train a physical information neural network model. In this tutorial, the following three aspects are introduced:
How to use sympy to define partial differential equation based on MindSpore Flow.
How to define the Dirichlet boundary conditions and the Neumann boundary conditions in a model.
How to train a physical information neural network using MindSpore functional programming paradigm.
Problem Description
Poisson’s equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson’s equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. We start from a 2-D homogeneous Poisson equation,
where u is the primary variable, f is the source term, and
We consider the source term f is a constant value and given (
In this case, the Dirichlet boundary condition and the Neumann boundary condition are used. The format is as follows:
Dirichlet boundary condition on the boundary of outside circle:
Neumann boundary condition on the boundary of inside circle:
In this case, the PINNs method is used to learn the mapping
Technology Path
MindSpore Flow solves the problem as follows:
Training Dataset Construction.
Model Construction.
Optimizer.
Poisson2D.
Model Training.
Model Evaluation and Visualization.
Importing the Required Packages
[1]:
import time
import matplotlib.pyplot as plt
import numpy as np
import sympy
from sympy import symbols, Function, diff
import mindspore as ms
from mindspore import nn, ops, Tensor, set_context, set_seed, jit
from mindspore import dtype as mstype
set_seed(123456)
set_context(mode=ms.GRAPH_MODE, device_target="GPU", device_id=0)
Training Dataset Construction
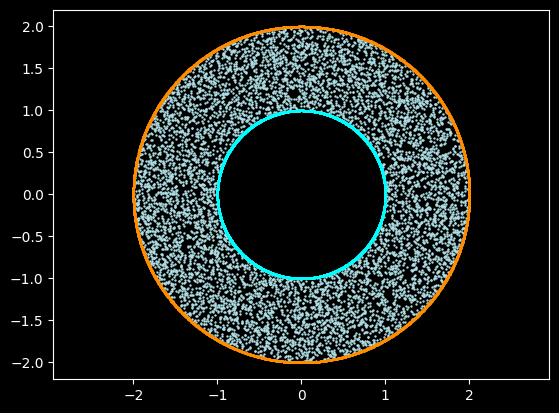
In this case, random sampling is performed according to the domain, initial condition and boundary condition to generate training data sets. Disk and CSGXOR are used to make a geometry with input and output boundaries, as well as domain. Download data construction Python script.
[2]:
from mindflow.geometry import generate_sampling_config, Disk, CSGXOR
class MyIterable:
def __init__(self, domain, bc_outer, bc_inner, bc_inner_normal):
self._index = 0
self._domain = domain.astype(np.float32)
self._bc_outer = bc_outer.astype(np.float32)
self._bc_inner = bc_inner.astype(np.float32)
self._bc_inner_normal = bc_inner_normal.astype(np.float32)
def __next__(self):
if self._index >= len(self._domain):
raise StopIteration
item = (self._domain[self._index], self._bc_outer[self._index], self._bc_inner[self._index],
self._bc_inner_normal[self._index])
self._index += 1
return item
def __iter__(self):
self._index = 0
return self
def __len__(self):
return len(self._domain)
def _get_region(config):
indisk_cfg = config["in_disk"]
in_disk = Disk(indisk_cfg["name"], (indisk_cfg["center_x"], indisk_cfg["center_y"]), indisk_cfg["radius"])
outdisk_cfg = config["out_disk"]
out_disk = Disk(outdisk_cfg["name"], (outdisk_cfg["center_x"], outdisk_cfg["center_y"]), outdisk_cfg["radius"])
union = CSGXOR(out_disk, in_disk)
return in_disk, out_disk, union
def create_training_dataset(config):
'''create_training_dataset'''
in_disk, out_disk, union = _get_region(config)
union.set_sampling_config(generate_sampling_config(config["data"]))
domain = union.sampling(geom_type="domain")
out_disk.set_sampling_config(generate_sampling_config(config["data"]))
bc_outer, _ = out_disk.sampling(geom_type="BC")
in_disk.set_sampling_config(generate_sampling_config(config["data"]))
bc_inner, bc_inner_normal = in_disk.sampling(geom_type="BC")
plt.figure()
plt.axis("equal")
plt.scatter(domain[:, 0], domain[:, 1], c="powderblue", s=0.5)
plt.scatter(bc_outer[:, 0], bc_outer[:, 1], c="darkorange", s=0.005)
plt.scatter(bc_inner[:, 0], bc_inner[:, 1], c="cyan", s=0.005)
plt.show()
dataset = ms.dataset.GeneratorDataset(source=MyIterable(domain, bc_outer, bc_inner, (-1.0) * bc_inner_normal),
column_names=["data", "bc_outer", "bc_inner", "bc_inner_normal"])
return dataset
def _numerical_solution(x, y):
return (4.0 - x ** 2 - y ** 2) / 4
def create_test_dataset(config):
"""create test dataset"""
_, _, union = _get_region(config)
union.set_sampling_config(generate_sampling_config(config["data"]))
test_data = union.sampling(geom_type="domain")
test_label = _numerical_solution(test_data[:, 0], test_data[:, 1]).reshape(-1, 1)
return test_data, test_label
The geometric shape of the generated data is a ring, the radius of the inner circle is 1.0, the radius of the outer circle is 2.0, and the amount of data in the boundary and domain is 8192. The generation parameters are set as follows:
[3]:
in_disk = {"name": "in_disk", "center_x": 0.0, "center_y": 0.0, "radius": 1.0}
out_disk = {"name": "out_disk", "center_x": 0.0, "center_y": 0.0, "radius": 2.0}
domain = {"size": 8192, "random_sampling": True, "sampler": "uniform"}
BC = {"size": 8192, "random_sampling": True, "sampler": "uniform", "with_normal": True}
data = {"domain": domain, "BC": BC}
config = {"in_disk": in_disk, "out_disk": out_disk, "data": data}
# create training dataset
dataset = create_training_dataset(config)
train_dataset = dataset.batch(batch_size=8192)
# create test dataset
inputs, label = create_test_dataset(config)
Model Construction
This example uses MultiScaleFCCell to construct a simple fully-connected network with a depth of 6 layers and the activation function is the tanh function. MultiScaleFCCell is imported from MindSpore Flow cell module.
[4]:
from mindflow.cell import MultiScaleFCCell
model = MultiScaleFCCell(in_channels=2,
out_channels=1,
layers=6,
neurons=128,
residual=False,
act="tanh",
num_scales=1)
Optimizer
Using Adaptive Moment Estimation (Adam) optimizer.
[5]:
optimizer = nn.Adam(model.trainable_params(), 0.001)
Poisson2D
The following Poisson2D includes the governing equations, Dirichlet boundary conditions, Norman boundary conditions, etc. The sympy is used for delineating partial differential equations in symbolic forms and computing all equations’ loss.
Symbol Declaration
Define x, y, and n to indicate the the horizontal coordinate, vertical coordinate, and normal vectors of inner circle boundary, respectively. The output u is a function related to x and y.
[6]:
x, y, n = symbols('x y n')
u = Function('u')(x, y)
# independent variables
in_vars = [x, y]
print("independent variables: ", in_vars)
# dependent variables
out_vars = [u]
print("dependent variables: ", out_vars)
independent variables: [x, y]
dependent variables: [u(x, y)]
Governing Equations
[7]:
govern_eq = diff(u, (x, 2)) + diff(u, (y, 2)) + 1.0
print("governing equation: ", govern_eq)
governing equation: Derivative(u(x, y), (x, 2)) + Derivative(u(x, y), (y, 2)) + 1.0
Dirichlet Boundary Condition
[8]:
bc_outer = u
print("bc_outer equation: ", bc_outer)
bc_outer equation: u(x, y)
Neumann Boundary Condition
[9]:
bc_inner = sympy.Derivative(u, n) - 0.5
print("bc_inner equation: ", bc_inner)
bc_inner equation: Derivative(u(x, y), n) - 0.5
The following Poisson2D problem is defined based on the Poisson base class combined with the governing equations and boundary conditions defined above. Download Poisson2D Python script.
[10]:
from mindflow.pde import Poisson, sympy_to_mindspore
class Poisson2D(Poisson):
def __init__(self, model, loss_fn="mse"):
super(Poisson2D, self).__init__(model, loss_fn=loss_fn)
self.bc_outer_nodes = sympy_to_mindspore(self.bc_outer(), self.in_vars, self.out_vars)
self.bc_inner_nodes = sympy_to_mindspore(self.bc_inner(), self.in_vars, self.out_vars)
def bc_outer(self):
bc_outer_eq = self.u
equations = {"bc_outer": bc_outer_eq}
return equations
def bc_inner(self):
bc_inner_eq = sympy.Derivative(self.u, self.normal) - 0.5
equations = {"bc_inner": bc_inner_eq}
return equations
def get_loss(self, pde_data, bc_outer_data, bc_inner_data, bc_inner_normal):
pde_res = self.parse_node(self.pde_nodes, inputs=pde_data)
pde_loss = self.loss_fn(pde_res[0], Tensor(np.array([0.0]), mstype.float32))
bc_inner_res = self.parse_node(self.bc_inner_nodes, inputs=bc_inner_data, norm=bc_inner_normal)
bc_inner_loss = self.loss_fn(bc_inner_res[0], Tensor(np.array([0.0]), mstype.float32))
bc_outer_res = self.parse_node(self.bc_outer_nodes, inputs=bc_outer_data)
bc_outer_loss = self.loss_fn(bc_outer_res[0], Tensor(np.array([0.0]), mstype.float32))
return pde_loss + bc_inner_loss + bc_outer_loss
problem = Poisson2D(model)
poisson: Derivative(u(x, y), (x, 2)) + Derivative(u(x, y), (y, 2)) + 1.0
Item numbers of current derivative formula nodes: 3
bc_outer: u(x, y)
Item numbers of current derivative formula nodes: 1
bc_inner: Derivative(u(x, y), n) - 0.5
Item numbers of current derivative formula nodes: 2
Model Training
With MindSpore version >= 2.0.0, we can use the functional programming for training neural networks. Download training Python script.
[11]:
# define forward function
def forward_fn(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal):
loss = problem.get_loss(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal)
return loss
# define grad function
grad_fn = ms.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=False)
# using jit to accelerate training
@jit
def train_step(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal):
loss, grads = grad_fn(pde_data, bc_outer_data, bc_inner_data, bc_inner_normal)
loss = ops.depend(loss, optimizer(grads))
return loss
Download the calculate function of training process in Python script.
[12]:
def _calculate_error(label, prediction):
'''calculate l2-error to evaluate accuracy'''
error = label - prediction
l2_error = np.sqrt(np.sum(np.square(error[..., 0]))) / np.sqrt(np.sum(np.square(label[..., 0])))
return l2_error
def _get_prediction(model, inputs, label_shape, batch_size):
'''calculate the prediction respect to the given inputs'''
prediction = np.zeros(label_shape)
prediction = prediction.reshape((-1, label_shape[1]))
inputs = inputs.reshape((-1, inputs.shape[1]))
time_beg = time.time()
index = 0
while index < inputs.shape[0]:
index_end = min(index + batch_size, inputs.shape[0])
test_batch = Tensor(inputs[index: index_end, :], mstype.float32)
prediction[index: index_end, :] = model(test_batch).asnumpy()
index = index_end
print(" predict total time: {} ms".format((time.time() - time_beg) * 1000))
prediction = prediction.reshape(label_shape)
prediction = prediction.reshape((-1, label_shape[1]))
return prediction
def calculate_l2_error(model, inputs, label, batch_size):
label_shape = label.shape
prediction = _get_prediction(model, inputs, label_shape, batch_size)
label = label.reshape((-1, label_shape[1]))
l2_error = _calculate_error(label, prediction)
print(" l2_error: ", l2_error)
print("==================================================================================================")
[13]:
epochs = 5000
steps_per_epochs = train_dataset.get_dataset_size()
sink_process = ms.data_sink(train_step, train_dataset, sink_size=1)
for epoch in range(1, epochs + 1):
# train
time_beg = time.time()
model.set_train(True)
for _ in range(steps_per_epochs):
step_train_loss = sink_process()
print(f"epoch: {epoch} train loss: {step_train_loss} epoch time: {(time.time() - time_beg)*1000 :.3f} ms")
model.set_train(False)
if epoch % 100 == 0:
# eval
calculate_l2_error(model, inputs, label, 8192)
epoch: 1 train loss: 1.2577767 epoch time: 6024.162 ms
epoch: 2 train loss: 1.2554792 epoch time: 70.884 ms
epoch: 3 train loss: 1.2534575 epoch time: 71.048 ms
epoch: 4 train loss: 1.2516733 epoch time: 100.632 ms
epoch: 5 train loss: 1.2503157 epoch time: 65.656 ms
epoch: 6 train loss: 1.2501826 epoch time: 137.487 ms
epoch: 7 train loss: 1.2511331 epoch time: 51.191 ms
epoch: 8 train loss: 1.2508672 epoch time: 65.980 ms
epoch: 9 train loss: 1.2503275 epoch time: 211.144 ms
epoch: 10 train loss: 1.2500556 epoch time: 224.515 ms
epoch: 11 train loss: 1.2500004 epoch time: 225.964 ms
epoch: 12 train loss: 1.2500298 epoch time: 220.117 ms
epoch: 13 train loss: 1.2500703 epoch time: 221.441 ms
epoch: 14 train loss: 1.2500948 epoch time: 220.214 ms
epoch: 15 train loss: 1.2500978 epoch time: 219.836 ms
epoch: 16 train loss: 1.250083 epoch time: 220.141 ms
epoch: 17 train loss: 1.2500567 epoch time: 229.682 ms
epoch: 18 train loss: 1.2500263 epoch time: 216.013 ms
epoch: 19 train loss: 1.2500005 epoch time: 218.639 ms
epoch: 20 train loss: 1.2499874 epoch time: 228.765 ms
epoch: 21 train loss: 1.2499917 epoch time: 230.179 ms
epoch: 22 train loss: 1.250007 epoch time: 215.476 ms
epoch: 23 train loss: 1.250018 epoch time: 224.334 ms
epoch: 24 train loss: 1.2500123 epoch time: 217.322 ms
epoch: 25 train loss: 1.249995 epoch time: 217.106 ms
epoch: 26 train loss: 1.249982 epoch time: 217.612 ms
epoch: 27 train loss: 1.249983 epoch time: 223.639 ms
epoch: 28 train loss: 1.2499921 epoch time: 226.419 ms
epoch: 29 train loss: 1.2499963 epoch time: 212.248 ms
epoch: 30 train loss: 1.2499878 epoch time: 225.295 ms
epoch: 31 train loss: 1.2499707 epoch time: 219.656 ms
epoch: 32 train loss: 1.2499548 epoch time: 218.019 ms
epoch: 33 train loss: 1.2499464 epoch time: 226.645 ms
epoch: 34 train loss: 1.2499409 epoch time: 222.399 ms
epoch: 35 train loss: 1.249928 epoch time: 224.290 ms
epoch: 36 train loss: 1.2499026 epoch time: 221.664 ms
epoch: 37 train loss: 1.2498704 epoch time: 221.300 ms
epoch: 38 train loss: 1.2498367 epoch time: 220.392 ms
epoch: 39 train loss: 1.2497979 epoch time: 221.848 ms
epoch: 40 train loss: 1.2497431 epoch time: 219.831 ms
epoch: 41 train loss: 1.2496608 epoch time: 217.333 ms
epoch: 42 train loss: 1.249544 epoch time: 220.116 ms
epoch: 43 train loss: 1.2493837 epoch time: 214.985 ms
epoch: 44 train loss: 1.2491598 epoch time: 220.717 ms
epoch: 45 train loss: 1.248828 epoch time: 216.047 ms
epoch: 46 train loss: 1.2483226 epoch time: 218.554 ms
epoch: 47 train loss: 1.247554 epoch time: 221.158 ms
epoch: 48 train loss: 1.2463655 epoch time: 218.594 ms
epoch: 49 train loss: 1.2444699 epoch time: 216.152 ms
epoch: 50 train loss: 1.2413855 epoch time: 220.306 ms
epoch: 51 train loss: 1.2362938 epoch time: 211.876 ms
epoch: 52 train loss: 1.2277732 epoch time: 213.732 ms
epoch: 53 train loss: 1.2135327 epoch time: 219.945 ms
epoch: 54 train loss: 1.1906419 epoch time: 217.820 ms
epoch: 55 train loss: 1.1573513 epoch time: 225.694 ms
epoch: 56 train loss: 1.1058999 epoch time: 221.004 ms
epoch: 57 train loss: 1.0343707 epoch time: 225.404 ms
epoch: 58 train loss: 0.9365865 epoch time: 224.163 ms
epoch: 59 train loss: 0.83171475 epoch time: 211.383 ms
epoch: 60 train loss: 0.77913564 epoch time: 229.284 ms
epoch: 61 train loss: 0.74204475 epoch time: 223.518 ms
epoch: 62 train loss: 0.80121577 epoch time: 229.029 ms
epoch: 63 train loss: 0.8549291 epoch time: 223.576 ms
epoch: 64 train loss: 0.7383551 epoch time: 235.727 ms
epoch: 65 train loss: 0.72710323 epoch time: 222.646 ms
epoch: 66 train loss: 0.6702794 epoch time: 226.154 ms
epoch: 67 train loss: 0.6987355 epoch time: 221.565 ms
epoch: 68 train loss: 0.6746455 epoch time: 234.406 ms
epoch: 69 train loss: 0.70462525 epoch time: 226.131 ms
epoch: 70 train loss: 0.67767555 epoch time: 229.177 ms
epoch: 71 train loss: 0.6821881 epoch time: 224.217 ms
epoch: 72 train loss: 0.64521456 epoch time: 223.717 ms
epoch: 73 train loss: 0.6368966 epoch time: 226.217 ms
epoch: 74 train loss: 0.592155 epoch time: 219.816 ms
epoch: 75 train loss: 0.6024764 epoch time: 214.097 ms
epoch: 76 train loss: 0.58170027 epoch time: 224.460 ms
epoch: 77 train loss: 0.5691892 epoch time: 223.964 ms
epoch: 78 train loss: 0.5925416 epoch time: 226.897 ms
epoch: 79 train loss: 0.61034954 epoch time: 221.710 ms
epoch: 80 train loss: 0.5831032 epoch time: 231.325 ms
epoch: 81 train loss: 0.5364084 epoch time: 222.517 ms
epoch: 82 train loss: 0.5502083 epoch time: 215.709 ms
epoch: 83 train loss: 0.5633007 epoch time: 209.054 ms
epoch: 84 train loss: 0.52546465 epoch time: 219.471 ms
epoch: 85 train loss: 0.53276706 epoch time: 218.961 ms
epoch: 86 train loss: 0.55396163 epoch time: 237.759 ms
epoch: 87 train loss: 0.5206229 epoch time: 219.588 ms
epoch: 88 train loss: 0.5106571 epoch time: 225.651 ms
epoch: 89 train loss: 0.53332406 epoch time: 224.282 ms
epoch: 90 train loss: 0.53076947 epoch time: 235.400 ms
epoch: 91 train loss: 0.5049336 epoch time: 215.371 ms
epoch: 92 train loss: 0.48215953 epoch time: 239.344 ms
epoch: 93 train loss: 0.4843874 epoch time: 218.674 ms
epoch: 94 train loss: 0.51292086 epoch time: 221.709 ms
epoch: 95 train loss: 0.56979203 epoch time: 225.018 ms
epoch: 96 train loss: 0.61994594 epoch time: 219.800 ms
epoch: 97 train loss: 0.4962491 epoch time: 223.785 ms
epoch: 98 train loss: 0.4802659 epoch time: 230.708 ms
epoch: 99 train loss: 0.54967964 epoch time: 221.209 ms
epoch: 100 train loss: 0.46414006 epoch time: 223.953 ms
predict total time: 124.87483024597168 ms
l2_error: 0.9584533008207833
==================================================================================================
...
epoch: 4901 train loss: 0.00012433846 epoch time: 241.115 ms
epoch: 4902 train loss: 0.00012422525 epoch time: 239.142 ms
epoch: 4903 train loss: 0.00012412701 epoch time: 234.900 ms
epoch: 4904 train loss: 0.00012404467 epoch time: 237.946 ms
epoch: 4905 train loss: 0.000123965 epoch time: 236.818 ms
epoch: 4906 train loss: 0.0001238766 epoch time: 255.728 ms
epoch: 4907 train loss: 0.00012378026 epoch time: 225.175 ms
epoch: 4908 train loss: 0.00012368544 epoch time: 241.107 ms
epoch: 4909 train loss: 0.00012359957 epoch time: 248.310 ms
epoch: 4910 train loss: 0.00012352059 epoch time: 239.238 ms
epoch: 4911 train loss: 0.0001234413 epoch time: 229.464 ms
epoch: 4912 train loss: 0.00012335769 epoch time: 228.504 ms
epoch: 4913 train loss: 0.00012327175 epoch time: 238.126 ms
epoch: 4914 train loss: 0.00012318943 epoch time: 236.290 ms
epoch: 4915 train loss: 0.00012311469 epoch time: 221.079 ms
epoch: 4916 train loss: 0.00012304715 epoch time: 238.825 ms
epoch: 4917 train loss: 0.00012298509 epoch time: 243.784 ms
epoch: 4918 train loss: 0.00012292914 epoch time: 235.416 ms
epoch: 4919 train loss: 0.00012288446 epoch time: 221.510 ms
epoch: 4920 train loss: 0.00012286083 epoch time: 244.597 ms
epoch: 4921 train loss: 0.00012286832 epoch time: 245.989 ms
epoch: 4922 train loss: 0.00012292268 epoch time: 234.209 ms
epoch: 4923 train loss: 0.00012304373 epoch time: 223.089 ms
epoch: 4924 train loss: 0.0001232689 epoch time: 234.764 ms
epoch: 4925 train loss: 0.00012365196 epoch time: 246.427 ms
epoch: 4926 train loss: 0.00012429312 epoch time: 233.304 ms
epoch: 4927 train loss: 0.0001253246 epoch time: 221.859 ms
epoch: 4928 train loss: 0.00012700919 epoch time: 230.224 ms
epoch: 4929 train loss: 0.00012967733 epoch time: 254.334 ms
epoch: 4930 train loss: 0.000134056 epoch time: 242.256 ms
epoch: 4931 train loss: 0.00014098533 epoch time: 225.075 ms
epoch: 4932 train loss: 0.00015257315 epoch time: 235.392 ms
epoch: 4933 train loss: 0.00017092828 epoch time: 243.934 ms
epoch: 4934 train loss: 0.00020245541 epoch time: 244.327 ms
epoch: 4935 train loss: 0.00025212576 epoch time: 238.360 ms
epoch: 4936 train loss: 0.00034049098 epoch time: 233.573 ms
epoch: 4937 train loss: 0.0004768648 epoch time: 242.150 ms
epoch: 4938 train loss: 0.0007306886 epoch time: 247.166 ms
epoch: 4939 train loss: 0.0011023732 epoch time: 242.486 ms
epoch: 4940 train loss: 0.001834287 epoch time: 237.257 ms
epoch: 4941 train loss: 0.0027812878 epoch time: 242.192 ms
epoch: 4942 train loss: 0.004766387 epoch time: 236.694 ms
epoch: 4943 train loss: 0.006648433 epoch time: 223.730 ms
epoch: 4944 train loss: 0.010807082 epoch time: 237.647 ms
epoch: 4945 train loss: 0.01206318 epoch time: 233.036 ms
epoch: 4946 train loss: 0.015489452 epoch time: 227.594 ms
epoch: 4947 train loss: 0.011565584 epoch time: 227.099 ms
epoch: 4948 train loss: 0.008471975 epoch time: 231.612 ms
epoch: 4949 train loss: 0.0035123175 epoch time: 276.854 ms
epoch: 4950 train loss: 0.00091841083 epoch time: 229.893 ms
epoch: 4951 train loss: 0.00053060305 epoch time: 231.533 ms
epoch: 4952 train loss: 0.0017638807 epoch time: 231.814 ms
epoch: 4953 train loss: 0.0035763814 epoch time: 236.456 ms
epoch: 4954 train loss: 0.004056363 epoch time: 244.743 ms
epoch: 4955 train loss: 0.0039708405 epoch time: 221.469 ms
epoch: 4956 train loss: 0.0027319128 epoch time: 236.732 ms
epoch: 4957 train loss: 0.0017904624 epoch time: 231.612 ms
epoch: 4958 train loss: 0.0009970744 epoch time: 244.820 ms
epoch: 4959 train loss: 0.00061692565 epoch time: 221.442 ms
epoch: 4960 train loss: 0.0007383662 epoch time: 245.430 ms
epoch: 4961 train loss: 0.0012403185 epoch time: 231.007 ms
epoch: 4962 train loss: 0.0018439001 epoch time: 233.718 ms
epoch: 4963 train loss: 0.0017326038 epoch time: 224.514 ms
epoch: 4964 train loss: 0.0011022249 epoch time: 237.367 ms
epoch: 4965 train loss: 0.00033718432 epoch time: 242.038 ms
epoch: 4966 train loss: 0.00018465787 epoch time: 230.688 ms
epoch: 4967 train loss: 0.00055812683 epoch time: 218.956 ms
epoch: 4968 train loss: 0.00085373345 epoch time: 239.294 ms
epoch: 4969 train loss: 0.0007744754 epoch time: 234.656 ms
epoch: 4970 train loss: 0.00047988302 epoch time: 243.434 ms
epoch: 4971 train loss: 0.0003720247 epoch time: 214.474 ms
epoch: 4972 train loss: 0.0004015266 epoch time: 239.108 ms
epoch: 4973 train loss: 0.00037753512 epoch time: 246.952 ms
epoch: 4974 train loss: 0.0002867286 epoch time: 235.668 ms
epoch: 4975 train loss: 0.00029258506 epoch time: 229.418 ms
epoch: 4976 train loss: 0.00041505875 epoch time: 239.248 ms
epoch: 4977 train loss: 0.00043451862 epoch time: 235.341 ms
epoch: 4978 train loss: 0.00030042438 epoch time: 236.248 ms
epoch: 4979 train loss: 0.00015146247 epoch time: 218.208 ms
epoch: 4980 train loss: 0.00016080803 epoch time: 246.693 ms
epoch: 4981 train loss: 0.00027215388 epoch time: 238.106 ms
epoch: 4982 train loss: 0.00031257677 epoch time: 236.889 ms
epoch: 4983 train loss: 0.0002639915 epoch time: 222.054 ms
epoch: 4984 train loss: 0.000204898 epoch time: 231.757 ms
epoch: 4985 train loss: 0.00019457101 epoch time: 246.356 ms
epoch: 4986 train loss: 0.00018954299 epoch time: 247.128 ms
epoch: 4987 train loss: 0.00016800698 epoch time: 219.524 ms
epoch: 4988 train loss: 0.00016529267 epoch time: 240.068 ms
epoch: 4989 train loss: 0.00019697993 epoch time: 235.206 ms
epoch: 4990 train loss: 0.00021988692 epoch time: 237.431 ms
epoch: 4991 train loss: 0.00019355604 epoch time: 219.045 ms
epoch: 4992 train loss: 0.00014973793 epoch time: 246.853 ms
epoch: 4993 train loss: 0.00013542885 epoch time: 226.068 ms
epoch: 4994 train loss: 0.00015176873 epoch time: 248.399 ms
epoch: 4995 train loss: 0.0001647438 epoch time: 217.880 ms
epoch: 4996 train loss: 0.00016070419 epoch time: 237.407 ms
epoch: 4997 train loss: 0.00015653059 epoch time: 235.727 ms
epoch: 4998 train loss: 0.00015907965 epoch time: 247.844 ms
epoch: 4999 train loss: 0.00015674165 epoch time: 226.864 ms
epoch: 5000 train loss: 0.00014248541 epoch time: 244.331 ms
predict total time: 1.7328262329101562 ms
l2_error: 0.00915682980750216
==================================================================================================
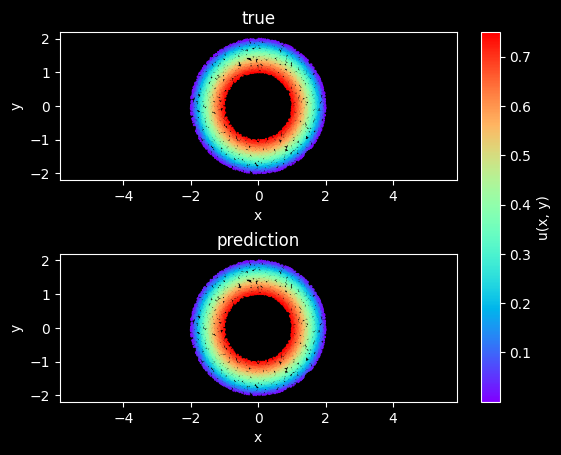
Model Evaluation and Visualization
After training, all data points in the flow field can be inferred. And related results can be visualized. Download visulization Python script.
[14]:
def visual(model, inputs, label, epochs=1):
'''visual result for poisson 2D'''
fig, ax = plt.subplots(2, 1)
ax = ax.flatten()
plt.subplots_adjust(hspace=0.5)
ax0 = ax[0].scatter(inputs[:, 0], inputs[:, 1], c=label[:, 0], cmap=plt.cm.rainbow, s=0.5)
ax[0].set_title("true")
ax[0].set_xlabel('x')
ax[0].set_ylabel('y')
ax[0].axis('equal')
ax[1].scatter(inputs[:, 0], inputs[:, 1], c=model(Tensor(inputs, mstype.float32)), cmap=plt.cm.rainbow, s=0.5)
ax[1].set_title("prediction")
ax[1].set_xlabel('x')
ax[1].set_ylabel('y')
ax[1].axis('equal')
cbar = fig.colorbar(ax0, ax=[ax[0], ax[1]])
cbar.set_label('u(x, y)')
plt.savefig(f"images/{epochs}-result.jpg", dpi=600)
[15]:
# visualization
visual(model, inputs, label, 5000)