PDE-Net for Convection-Diffusion Equation

  

Overview

PDE-Net is a feedforward deep network proposed by Zichao Long et al. to learn partial differential equations from data, predict the dynamic characteristics of complex systems accurately and uncover potential PDE models. The basic idea of PDE-Net is to approximate differential operators by learning convolution kernels (filters). Neural networks or other machine learning methods are applied to fit unknown nonlinear responses. Numerical experiments show that the model can identify the observed dynamical equations and predict the dynamical behavior over a relatively long period of time, even in noisy environments. More information can be found in PDE-Net: Learning PDEs from Data.

This notebook requires MindSpore version >= 2.0.0 to support new APIs including: mindspore.jit, mindspore.jit_class, mindspore.data_sink.

Problem Description

This case solves the inverse problem of convection-diffusion partial differential equations with variable parameters and realizes long-term prediction.

Governing Equation

In this case, the convection-diffusion equation is of the form:

\[u_t = a(x,y) u_x + b(x,y) u_y + c u_{xx} + d u_{yy}, \quad (x,y) \in[0,2 \pi] \times[0,2 \pi]\]

\[u|_{t=0} = u_0(x,y)\]

The coefficients of each derivative are:

\[a(x,y)=0.5(cos(y)+x(2\pi-x)sin(x))+0.6 \quad b(x,y)=2(cos(y)+sin(x))+0.8\]

\[c=0.2 \quad d=0.3\]

Model Structure of the PDE-Net

The PDE-Net consists of multiple \(\delta T\) Blocks in series to implement prediction of long sequence information. Each \(\delta T\) Block includes several moment matrixes of trainable parameters. The matrixes can be converted to convolution kernels according to a mapping relationship. Thereby the derivatives of the physical field can be obtained. After linearly combining the derivative and its corresponding physical quantity, the information of the next time step can be deduced by using the forward Euler method.

Technology Path

MindSpore Flow solves the problem as follows:

1. Model Construction.

2. Single Step Training.

3. Multi-step Training.

4. Model Evaluation and Visualization.

import os
import time
import numpy as np

import mindspore
from mindspore.common import set_seed
from mindspore import nn, Tensor, ops, jit
from mindspore.train.serialization import load_param_into_net

The following src pacakage can be downloaded in applications/data_mechanism_fusion/pde_net/src.

from mindflow.cell import PDENet
from mindflow.utils import load_yaml_config
from mindflow.loss import get_loss_metric, RelativeRMSELoss
from mindflow.pde import UnsteadyFlowWithLoss

from src import init_model, create_dataset, calculate_lp_loss_error
from src import make_dir, scheduler, get_param_dic
from src import plot_coe, plot_extrapolation_error, get_label_coe, plot_test_error

Parameter can be modified in configuration file.

set_seed(0)
np.random.seed(0)
mindspore.set_context(mode=mindspore.GRAPH_MODE, device_target="GPU", device_id=3)

# load configuration yaml
config = load_yaml_config('pde_net.yaml')

Model Construction

MindSpore Flow provides the PDENet interface to directly create a PDE-Net model. You need to specify the width, height, data depth, boundary condition, and highest order of fitting.

def init_model(config):
    return PDENet(height=config["mesh_size"],
                  width=config["mesh_size"],
                  channels=config["channels"],
                  kernel_size=config["kernel_size"],
                  max_order=config["max_order"],
                  dx=2 * np.pi / config["mesh_size"],
                  dy=2 * np.pi / config["mesh_size"],
                  dt=config["dt"],
                  periodic=config["perodic_padding"],
                  enable_moment=config["enable_moment"],
                  if_fronzen=config["if_frozen"],
                  )

Single Step Training

The parameters of each \(\delta T\) block are shared. Therefore, the model is trained one by one based on the number of connected \(\delta T\) blocks. When step is 1, the model is in the warm-up phase. The moments of the PDE-Net are frozen. The parameters in the moments are not involved in training. Each time a \(\delta T\) block is added, the program generates data and reads data sets. After the model is initialized, the program loads the checkpoint trained in the previous step, defines the optimizer, mode, and loss function. During training process, the model reflects the model performance in real time based on the callback function.

def train_single_step(step, config, lr, train_dataset, eval_dataset):
    """train PDE-Net with advancing steps"""

    print("Current step for train loop: {}".format(step, ))
    model = init_model(config)

    epoch = config["epochs"]
    warm_up_epoch_scale = 10
    if step == 1:
        model.if_fronzen = True
        epoch = warm_up_epoch_scale * epoch
    elif step == 2:
        param_dict = get_param_dic(config["summary_dir"], step - 1, epoch * 10)
        load_param_into_net(model, param_dict)
        print("Load pre-trained model successfully")
    else:
        param_dict = get_param_dic(config["summary_dir"], step - 1, epoch)
        load_param_into_net(model, param_dict)
        print("Load pre-trained model successfully")

    optimizer = nn.Adam(model.trainable_params(), learning_rate=Tensor(lr))
    problem = UnsteadyFlowWithLoss(model, t_out=step, loss_fn=RelativeRMSELoss(), data_format="NTCHW")

    def forward_fn(u0, uT):
        loss = problem.get_loss(u0, uT)
        return loss

    grad_fn = mindspore.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=False)

    @jit
    def train_step(u0, uT):
        loss, grads = grad_fn(u0, uT)
        loss = ops.depend(loss, optimizer(grads))
        return loss

    steps = train_dataset.get_dataset_size()
    sink_process = mindspore.data_sink(train_step, train_dataset, sink_size=1)

    for cur_epoch in range(epoch):
        local_time_beg = time.time()
        model.set_train()

        for _ in range(steps):
            cur_loss = sink_process()
            print("epoch: %s, loss is %s" % (cur_epoch + 1, cur_loss), flush=True)
        local_time_end = time.time()
        epoch_seconds = (local_time_end - local_time_beg) * 1000
        step_seconds = epoch_seconds / steps
        print("Train epoch time: {:5.3f} ms, per step time: {:5.3f} ms".format
              (epoch_seconds, step_seconds), flush=True)

        if (cur_epoch + 1) % config["save_epoch_interval"] == 0:
            ckpt_file_name = "ckpt/step_{}".format(step)
            ckpt_dir = os.path.join(config["summary_dir"], ckpt_file_name)
            if not os.path.exists(ckpt_dir):
                make_dir(ckpt_dir)
            ckpt_name = "pdenet-{}.ckpt".format(cur_epoch + 1, )
            mindspore.save_checkpoint(model, os.path.join(ckpt_dir, ckpt_name))

        if (cur_epoch + 1) % config['eval_interval'] == 0:
            calculate_lp_loss_error(problem, eval_dataset, config["batch_size"])

Multi-step Training

The PDE-Net is trained step by step. With MindSpore version >= 2.0.0, we can use the functional programming for training neural networks.

def train(config):
    lr = config["lr"]
    for i in range(1, config["multi_step"] + 1):
        db_name = "train_step{}.mindrecord".format(i)
        dataset = create_dataset(config, i, db_name, "train", data_size=2 * config["batch_size"])
        train_dataset, eval_dataset = dataset.create_train_dataset()
        lr = scheduler(int(config["multi_step"] / config["learning_rate_reduce_times"]), step=i, lr=lr)
        train_single_step(step=i, config=config, lr=lr, train_dataset=train_dataset, eval_dataset=eval_dataset)

if not os.path.exists(config["mindrecord_data_dir"]):
    make_dir(config["mindrecord_data_dir"])
train(config)

Mindrecorder saved
Current step for train loop: 1
epoch: 1, loss is 313.45258
Train epoch time: 7294.444 ms, per step time: 7294.444 ms
epoch: 2, loss is 283.09055
Train epoch time: 15.857 ms, per step time: 15.857 ms
epoch: 3, loss is 292.2815
Train epoch time: 16.684 ms, per step time: 16.684 ms
epoch: 4, loss is 300.3354
Train epoch time: 18.559 ms, per step time: 18.559 ms
epoch: 5, loss is 295.53436
Train epoch time: 16.430 ms, per step time: 16.430 ms
epoch: 6, loss is 289.45068
Train epoch time: 8.752 ms, per step time: 8.752 ms
epoch: 7, loss is 297.86658
Train epoch time: 10.015 ms, per step time: 10.015 ms
epoch: 8, loss is 269.71762
Train epoch time: 9.050 ms, per step time: 9.050 ms
epoch: 9, loss is 298.23706
Train epoch time: 8.361 ms, per step time: 8.361 ms
epoch: 10, loss is 271.063
Train epoch time: 8.056 ms, per step time: 8.056 ms
================================Start Evaluation================================
LpLoss_error: 15.921201
=================================End Evaluation=================================
...
predict total time: 0.6082212924957275 s
epoch: 491, loss is 0.6402923
Train epoch time: 135.562 ms, per step time: 135.562 ms
epoch: 492, loss is 0.64142
Train epoch time: 115.278 ms, per step time: 115.278 ms
epoch: 493, loss is 0.61553574
Train epoch time: 119.042 ms, per step time: 119.042 ms
epoch: 494, loss is 0.644715
Train epoch time: 111.061 ms, per step time: 111.061 ms
epoch: 495, loss is 0.64503396
Train epoch time: 120.771 ms, per step time: 120.771 ms
epoch: 496, loss is 0.6481593
Train epoch time: 111.252 ms, per step time: 111.252 ms
epoch: 497, loss is 0.6493112
Train epoch time: 110.378 ms, per step time: 110.378 ms
epoch: 498, loss is 0.6368339
Train epoch time: 111.505 ms, per step time: 111.505 ms
epoch: 499, loss is 0.6521274
Train epoch time: 113.217 ms, per step time: 113.217 ms
epoch: 500, loss is 0.65510833
Train epoch time: 115.729 ms, per step time: 115.729 ms
================================Start Evaluation================================
LpLoss_error: 0.040348217
=================================End Evaluation=================================
predict total time: 0.6067502498626709 s

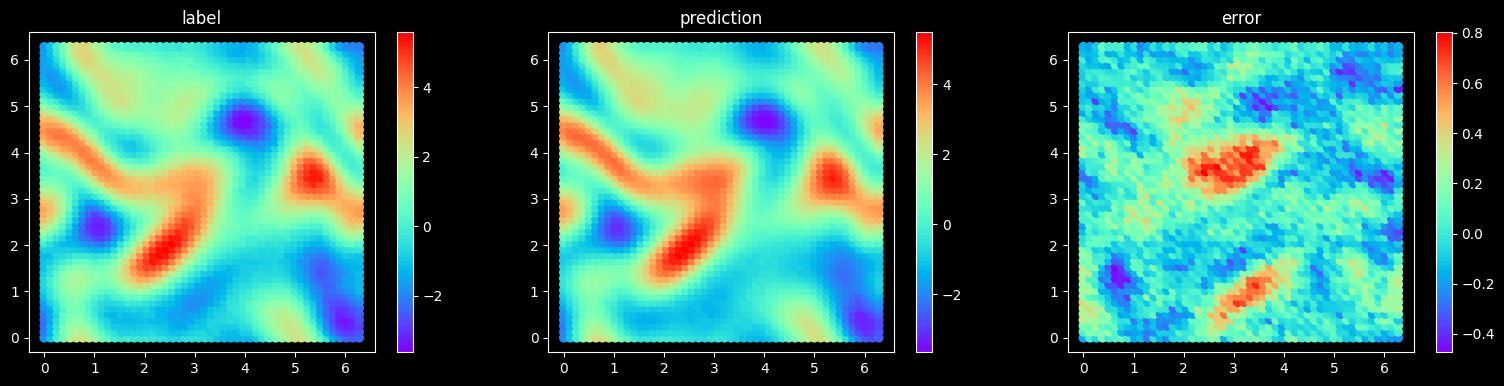
Model Evaluation and Visualization

After the model training is complete, the following figure shows the comparison between the prediction result and label.

step = 20
test_data_size = 20

model = init_model(config)
param_dict = get_param_dic(config["summary_dir"], config["multi_step"], config["epochs"])
load_param_into_net(model, param_dict)

[]

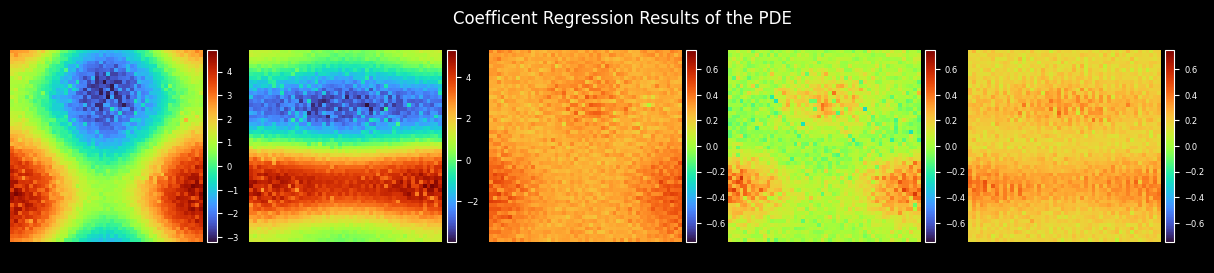
Plot Coefficient

coe_label = get_label_coe(max_order=config["max_order"], resolution=config["mesh_size"])
coes_out_dir = os.path.join(config["figure_out_dir"], "coes")
plot_coe(model.coe, coes_out_dir, prefix="coe_trained", step=step, title="Coefficient Regression Results of the PDE")
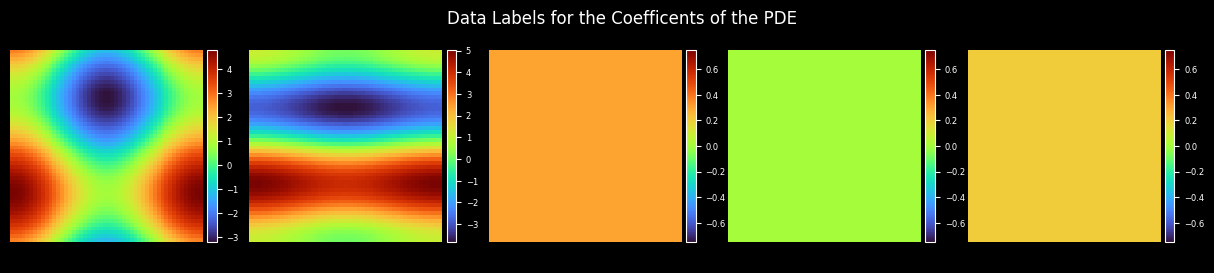
plot_coe(coe_label, coes_out_dir, prefix="coe_label", title="Data Labels for the Coefficients of the PDE")

Plot Test Error

dataset = create_dataset(config, step, "eval.mindrecord", "test", data_size=test_data_size)
test_dataset = dataset.create_test_dataset(step)
iterator_test_dataset = test_dataset.create_dict_iterator()
final_item = [_ for _ in iterator_test_dataset][-1]
plot_test_error(problem, get_loss_metric("mse"), final_item, step, config["mesh_size"], config["figure_out_dir"])

Mindrecorder saved
sample 20, MSE Loss 0.061236363

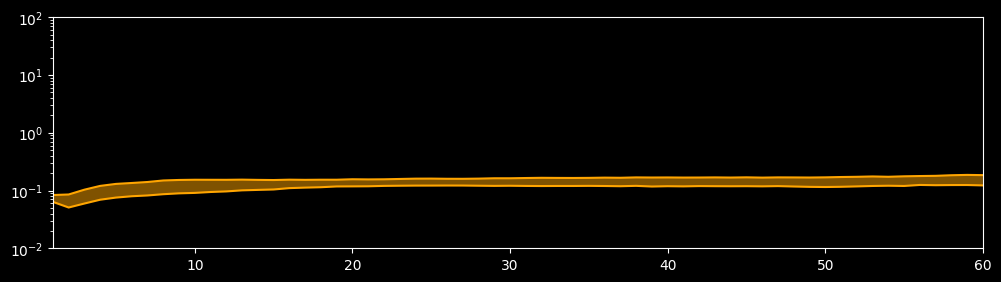
Plot Extrapolation Error

max_step = 60
sample_size = 40

dataset = create_dataset(config, max_step, "extrapolation.mindrecord", "test", data_size=sample_size)
plot_extrapolation_error(config, dataset, max_step=max_step)

Mindrecorder saved
step = 1, p25 = 0.06405, p75 = 0.08643
step = 2, p25 = 0.05012, p75 = 0.08393
step = 3, p25 = 0.06112, p75 = 0.10304
step = 4, p25 = 0.06977, p75 = 0.11740
step = 5, p25 = 0.07448, p75 = 0.12558
step = 6, p25 = 0.07964, p75 = 0.13329
step = 7, p25 = 0.08389, p75 = 0.14144
step = 8, p25 = 0.08721, p75 = 0.14411
step = 9, p25 = 0.08933, p75 = 0.14618
step = 10, p25 = 0.09413, p75 = 0.14660
step = 11, p25 = 0.09456, p75 = 0.14647
step = 12, p25 = 0.09532, p75 = 0.15166
step = 13, p25 = 0.09663, p75 = 0.15069
step = 14, p25 = 0.10087, p75 = 0.14878
step = 15, p25 = 0.10134, p75 = 0.14877
step = 16, p25 = 0.10700, p75 = 0.14848
step = 17, p25 = 0.10862, p75 = 0.15084
step = 18, p25 = 0.11188, p75 = 0.15105
step = 19, p25 = 0.11380, p75 = 0.15106
step = 20, p25 = 0.11437, p75 = 0.15068
step = 21, p25 = 0.11436, p75 = 0.15261
step = 22, p25 = 0.11572, p75 = 0.15087
step = 23, p25 = 0.11534, p75 = 0.15267
step = 24, p25 = 0.11588, p75 = 0.15540
step = 25, p25 = 0.11642, p75 = 0.15679
step = 26, p25 = 0.11598, p75 = 0.15700
step = 27, p25 = 0.11619, p75 = 0.15895
step = 28, p25 = 0.11611, p75 = 0.16042
step = 29, p25 = 0.11668, p75 = 0.16299
step = 30, p25 = 0.11663, p75 = 0.16413
step = 31, p25 = 0.11826, p75 = 0.16518
step = 32, p25 = 0.11898, p75 = 0.16673
step = 33, p25 = 0.11977, p75 = 0.16929
step = 34, p25 = 0.12110, p75 = 0.16919
step = 35, p25 = 0.12041, p75 = 0.17030
step = 36, p25 = 0.12223, p75 = 0.17150
step = 37, p25 = 0.12190, p75 = 0.17301
step = 38, p25 = 0.12270, p75 = 0.17389
step = 39, p25 = 0.12147, p75 = 0.17460
step = 40, p25 = 0.12005, p75 = 0.17384
step = 41, p25 = 0.12144, p75 = 0.17257
step = 42, p25 = 0.11986, p75 = 0.17334
step = 43, p25 = 0.11940, p75 = 0.17336
step = 44, p25 = 0.12085, p75 = 0.17301
step = 45, p25 = 0.11940, p75 = 0.17372
step = 46, p25 = 0.11919, p75 = 0.17274
step = 47, p25 = 0.12200, p75 = 0.17317
step = 48, p25 = 0.12044, p75 = 0.17336
step = 49, p25 = 0.12178, p75 = 0.17478
step = 50, p25 = 0.12355, p75 = 0.17511
step = 51, p25 = 0.12578, p75 = 0.17709
step = 52, p25 = 0.12434, p75 = 0.17895
step = 53, p25 = 0.12512, p75 = 0.18118
step = 54, p25 = 0.12532, p75 = 0.17828
step = 55, p25 = 0.12323, p75 = 0.18043
step = 56, p25 = 0.12300, p75 = 0.17973
step = 57, p25 = 0.12319, p75 = 0.17869
step = 58, p25 = 0.12315, p75 = 0.17695
step = 59, p25 = 0.12245, p75 = 0.17721
step = 60, p25 = 0.12120, p75 = 0.17679