PeRCNN for 2D burgers Equation
Overview
PDE equations occupy an important position in the modeling of physical systems. But many underlying PDEs have not yet been fully explored in epidemiology, meteorological science, fluid mechanics, and biology. However, for those known PDE equations, such as Naiver-Stokes equations, the exact numerical calculation of these equations requires huge computing power, which hinders the application of numerical simulation in large-scale systems. Recently, advances in machine learning provide a new way for PDE solution and inversion.
Recently, Huawei and Professor Sun Hao’s team from Renmin University of China proposed Physics-encoded Recurrent Convolutional Neural Network, PeRCNN based on Ascend platform and MindSpore. Compared with physical information neural network, ConvLSTM, PDE-NET and other methods, generalization and noise resistance of PeRCNN are significantly improved. The long-term prediction accuracy is improved by more than 10 times. This method has broad application prospects in aerospace, shipbuilding, weather forecasting and other fields. The results have been published in nature machine intelligence.
Problem Description
Burgers’ equation is a nonlinear partial differential equation that simulates the propagation and reflection of shock waves. It is widely used in the fields of fluid mechanics, nonlinear acoustics, gas dynamics et al. It is named after Johannes Martins Hamburg (1895-1981). In this case, the 2D Burgers’ equation with viscosity is solved based on PeRCNN method.
Governing Equation
In this research, Burgers Equation is formulted as follow:
where, \(\nu = 0.005\)
Technology Path
MindSpore Flow solves the problem as follows:
Optimizer and One-step Training
Model Construction
Model training
Model Evaluation and Visualization.
[7]:
import os
import time
import numpy as np
[8]:
from mindspore import context, jit, nn, ops, save_checkpoint, set_seed
import mindspore.common.dtype as mstype
from mindflow.utils import load_yaml_config, print_log
from src import RecurrentCNNCell, RecurrentCNNCellBurgers, Trainer, UpScaler, post_process
[9]:
set_seed(123456)
np.random.seed(123456)
context.set_context(mode=context.GRAPH_MODE, device_target="GPU", device_id=0)
[11]:
# load configuration yaml
config = load_yaml_config('./configs/data_driven_percnn_burgers.yaml')
Optimizer and One-step Training
[20]:
def train_stage(trainer, stage, pattern, config, ckpt_dir, use_ascend):
"""train stage"""
if use_ascend:
from mindspore.amp import DynamicLossScaler, all_finite
loss_scaler = DynamicLossScaler(2**10, 2, 100)
if 'milestone_num' in config.keys():
milestone = list([(config['epochs']//config['milestone_num'])*(i + 1)
for i in range(config['milestone_num'])])
learning_rate = config['learning_rate']
lr = float(config['learning_rate'])*np.array(list([config['gamma']
** i for i in range(config['milestone_num'])]))
learning_rate = nn.piecewise_constant_lr(milestone, list(lr))
else:
learning_rate = config['learning_rate']
if stage == 'pretrain':
params = trainer.upconv.trainable_params()
else:
params = trainer.upconv.trainable_params() + trainer.recurrent_cnn.trainable_params()
optimizer = nn.Adam(params, learning_rate=learning_rate)
def forward_fn():
if stage == 'pretrain':
loss = trainer.get_ic_loss()
else:
loss = trainer.get_loss()
if use_ascend:
loss = loss_scaler.scale(loss)
return loss
if stage == 'pretrain':
grad_fn = ops.value_and_grad(forward_fn, None, params, has_aux=False)
else:
grad_fn = ops.value_and_grad(forward_fn, None, params, has_aux=True)
@jit
def train_step():
loss, grads = grad_fn()
if use_ascend:
loss = loss_scaler.unscale(loss)
is_finite = all_finite(grads)
if is_finite:
grads = loss_scaler.unscale(grads)
loss = ops.depend(loss, optimizer(grads))
loss_scaler.adjust(is_finite)
else:
loss = ops.depend(loss, optimizer(grads))
return loss
best_loss = 100000
for epoch in range(1, 1 + config['epochs']):
time_beg = time.time()
trainer.upconv.set_train(True)
trainer.recurrent_cnn.set_train(True)
if stage == 'pretrain':
step_train_loss = train_step()
print_log(
f"epoch: {epoch} train loss: {step_train_loss} \
epoch time: {(time.time() - time_beg)*1000 :5.3f}ms \
step time: {(time.time() - time_beg)*1000 :5.3f}ms")
else:
step_train_loss, loss_data, loss_ic, loss_phy, loss_valid = train_step()
print_log(f"epoch: {epoch} train loss: {step_train_loss} ic_loss: {loss_ic} data_loss: {loss_data}"
f"val_loss: {loss_valid} phy_loss: {loss_phy}"
f"epoch time: {(time.time() - time_beg)*1000 :5.3f}ms"
f"step time: {(time.time() - time_beg)*1000 :5.3f}ms")
if step_train_loss < best_loss:
best_loss = step_train_loss
print_log('best loss', best_loss, 'save model')
save_checkpoint(trainer.upconv, os.path.join(ckpt_dir, f"{pattern}_{config['name']}_upconv.ckpt"))
save_checkpoint(trainer.recurrent_cnn,
os.path.join(ckpt_dir, f"{pattern}_{config['name']}_recurrent_cnn.ckpt"))
if pattern == 'physics_driven':
trainer.recurrent_cnn.show_coef()
Model Construction
PeRCNN is composed of two networks which are UpSclaer for upscaling and recurrent CNN as a backbone.
[23]:
def train():
"""train"""
burgers_config = config
use_ascend = context.get_context(attr_key='device_target') == "Ascend"
print_log(f"use_ascend: {use_ascend}")
if use_ascend:
compute_dtype = mstype.float16
else:
compute_dtype = mstype.float32
data_config = burgers_config['data']
optimizer_config = burgers_config['optimizer']
model_config = burgers_config['model']
summary_config = burgers_config['summary']
upconv = UpScaler(in_channels=model_config['in_channels'],
out_channels=model_config['out_channels'],
hidden_channels=model_config['upscaler_hidden_channels'],
kernel_size=model_config['kernel_size'],
stride=model_config['stride'],
has_bais=True)
if use_ascend:
from mindspore.amp import auto_mixed_precision
auto_mixed_precision(upconv, 'O1')
pattern = data_config['pattern']
if pattern == 'data_driven':
recurrent_cnn = RecurrentCNNCell(input_channels=model_config['in_channels'],
hidden_channels=model_config['rcnn_hidden_channels'],
kernel_size=model_config['kernel_size'],
compute_dtype=compute_dtype)
else:
recurrent_cnn = RecurrentCNNCellBurgers(kernel_size=model_config['kernel_size'],
init_coef=model_config['init_coef'],
compute_dtype=compute_dtype)
percnn_trainer = Trainer(upconv=upconv,
recurrent_cnn=recurrent_cnn,
timesteps_for_train=data_config['rollout_steps'],
dx=data_config['dx'],
dt=data_config['dy'],
nu=data_config['nu'],
data_path=os.path.join(data_config['root_dir'], data_config['file_name']),
compute_dtype=compute_dtype)
ckpt_dir = os.path.join(summary_config["root_dir"], summary_config['ckpt_dir'])
if not os.path.exists(ckpt_dir):
os.makedirs(ckpt_dir)
train_stage(percnn_trainer, 'pretrain', pattern, optimizer_config['pretrain'], ckpt_dir, use_ascend)
train_stage(percnn_trainer, 'finetune', pattern, optimizer_config['finetune'], ckpt_dir, use_ascend)
post_process(percnn_trainer, pattern)
Model Training
With MindSpore version >= 2.0.0, we can use the functional programming for training neural networks.
[24]:
train()
use_ascend: False
epoch: 1 train loss: 1.5724593 epoch time: 0.867 s
epoch: 2 train loss: 1.5299724 epoch time: 0.002 s
epoch: 3 train loss: 1.4901378 epoch time: 0.002 s
epoch: 4 train loss: 1.449844 epoch time: 0.002 s
epoch: 5 train loss: 1.4070688 epoch time: 0.002 s
epoch: 6 train loss: 1.3605155 epoch time: 0.002 s
epoch: 7 train loss: 1.3093143 epoch time: 0.002 s
epoch: 8 train loss: 1.253143 epoch time: 0.002 s
epoch: 9 train loss: 1.1923409 epoch time: 0.002 s
epoch: 10 train loss: 1.1278089 epoch time: 0.002 s
...
epoch: 5862 train loss: 0.00017873458 epoch time: 0.001 s
epoch: 5863 train loss: 0.00017868946 epoch time: 0.001 s
epoch: 5864 train loss: 0.00017864427 epoch time: 0.001 s
epoch: 5865 train loss: 0.00017859896 epoch time: 0.001 s
epoch: 5866 train loss: 0.00017855378 epoch time: 0.001 s
epoch: 5867 train loss: 0.00017850856 epoch time: 0.001 s
epoch: 5868 train loss: 0.00017846328 epoch time: 0.001 s
epoch: 5869 train loss: 0.00017841818 epoch time: 0.001 s
epoch: 5870 train loss: 0.000178373 epoch time: 0.001 s
epoch: 5871 train loss: 0.0001783278 epoch time: 0.001 s
...
epoch: 1 train loss: 0.0040010856 ic_loss: 0.00017339904 data_loss: 0.0036542874 val_loss: 0.034989584 phy_loss: 385.93723 epoch time: 14.898 s
best loss 0.0040010856 save model
epoch: 2 train loss: 0.023029208 ic_loss: 0.0069433 data_loss: 0.009142607 val_loss: 0.035638213 phy_loss: 416.80725 epoch time: 0.247 s
epoch: 3 train loss: 0.09626201 ic_loss: 0.030940203 data_loss: 0.0343816 val_loss: 0.05810566 phy_loss: 221.00093 epoch time: 0.162 s
epoch: 4 train loss: 0.01788263 ic_loss: 0.0053461124 data_loss: 0.0071904045 val_loss: 0.03353381 phy_loss: 301.05966 epoch time: 0.147 s
epoch: 5 train loss: 0.029557336 ic_loss: 0.0091625415 data_loss: 0.011232254 val_loss: 0.038305752 phy_loss: 449.9107 epoch time: 0.152 s
epoch: 6 train loss: 0.052337468 ic_loss: 0.016626468 data_loss: 0.019084534 val_loss: 0.046096146 phy_loss: 497.9761 epoch time: 0.214 s
epoch: 7 train loss: 0.014262615 ic_loss: 0.004195284 data_loss: 0.005872047 val_loss: 0.03377932 phy_loss: 430.3675 epoch time: 0.151 s
epoch: 8 train loss: 0.00919872 ic_loss: 0.0025033113 data_loss: 0.0041920976 val_loss: 0.031886213 phy_loss: 344.02713 epoch time: 0.181 s
epoch: 9 train loss: 0.032457784 ic_loss: 0.010022995 data_loss: 0.012411795 val_loss: 0.039276786 phy_loss: 301.3161 epoch time: 0.168 s
epoch: 10 train loss: 0.027750801 ic_loss: 0.008489873 data_loss: 0.010771056 val_loss: 0.037965972 phy_loss: 310.4488 epoch time: 0.159 s
...
epoch: 14991 train loss: 0.0012423343 ic_loss: 0.00041630908 data_loss: 0.00040971604 val_loss: 0.03190168 phy_loss: 394.9725 epoch time: 0.163 s
best loss 0.0012423343 save model
epoch: 14992 train loss: 0.0012423296 ic_loss: 0.0004163079 data_loss: 0.00040971374 val_loss: 0.0319017 phy_loss: 394.97614 epoch time: 0.158 s
best loss 0.0012423296 save model
epoch: 14993 train loss: 0.0012423252 ic_loss: 0.00041630593 data_loss: 0.00040971336 val_loss: 0.031901684 phy_loss: 394.97284 epoch time: 0.196 s
best loss 0.0012423252 save model
epoch: 14994 train loss: 0.0012423208 ic_loss: 0.00041630483 data_loss: 0.00040971107 val_loss: 0.0319017 phy_loss: 394.97568 epoch time: 0.173 s
best loss 0.0012423208 save model
epoch: 14995 train loss: 0.0012423162 ic_loss: 0.0004163029 data_loss: 0.00040971037 val_loss: 0.031901684 phy_loss: 394.97305 epoch time: 0.194 s
best loss 0.0012423162 save model
epoch: 14996 train loss: 0.0012423118 ic_loss: 0.00041630171 data_loss: 0.00040970836 val_loss: 0.031901695 phy_loss: 394.9754 epoch time: 0.175 s
best loss 0.0012423118 save model
epoch: 14997 train loss: 0.0012423072 ic_loss: 0.0004162999 data_loss: 0.00040970749 val_loss: 0.031901684 phy_loss: 394.97308 epoch time: 0.164 s
best loss 0.0012423072 save model
epoch: 14998 train loss: 0.0012423028 ic_loss: 0.00041629872 data_loss: 0.00040970545 val_loss: 0.0319017 phy_loss: 394.97534 epoch time: 0.135 s
best loss 0.0012423028 save model
epoch: 14999 train loss: 0.0012422984 ic_loss: 0.00041629683 data_loss: 0.00040970472 val_loss: 0.031901687 phy_loss: 394.97314 epoch time: 0.135 s
best loss 0.0012422984 save model
epoch: 15000 train loss: 0.0012422939 ic_loss: 0.00041629552 data_loss: 0.00040970283 val_loss: 0.0319017 phy_loss: 394.97556 epoch time: 0.153 s
best loss 0.0012422939 save model
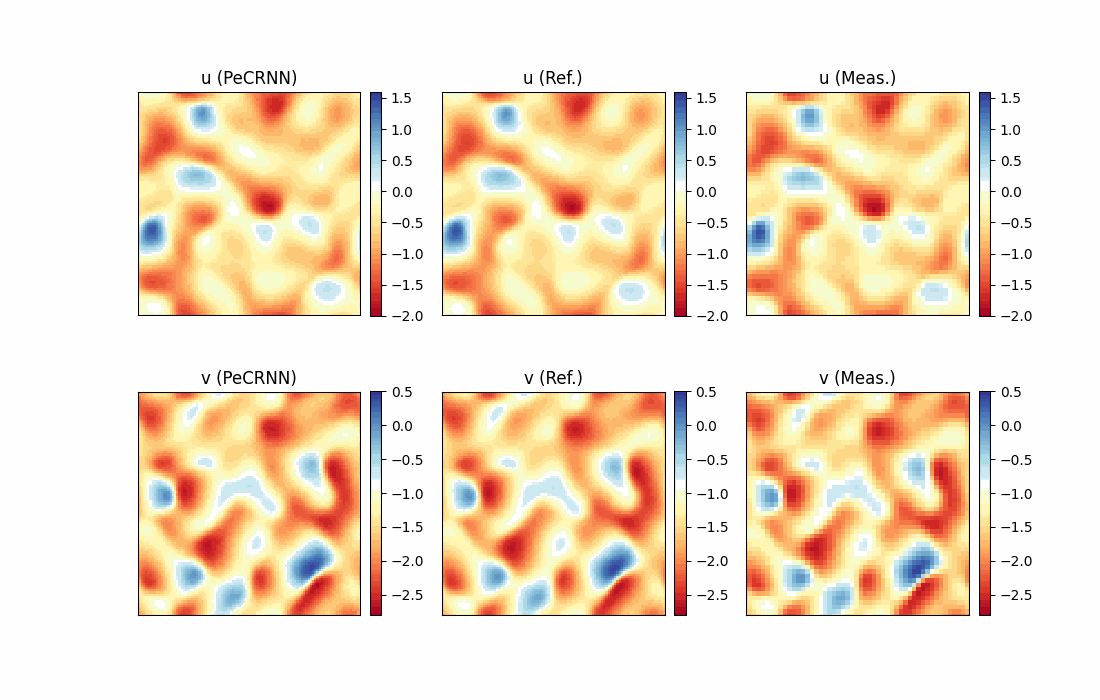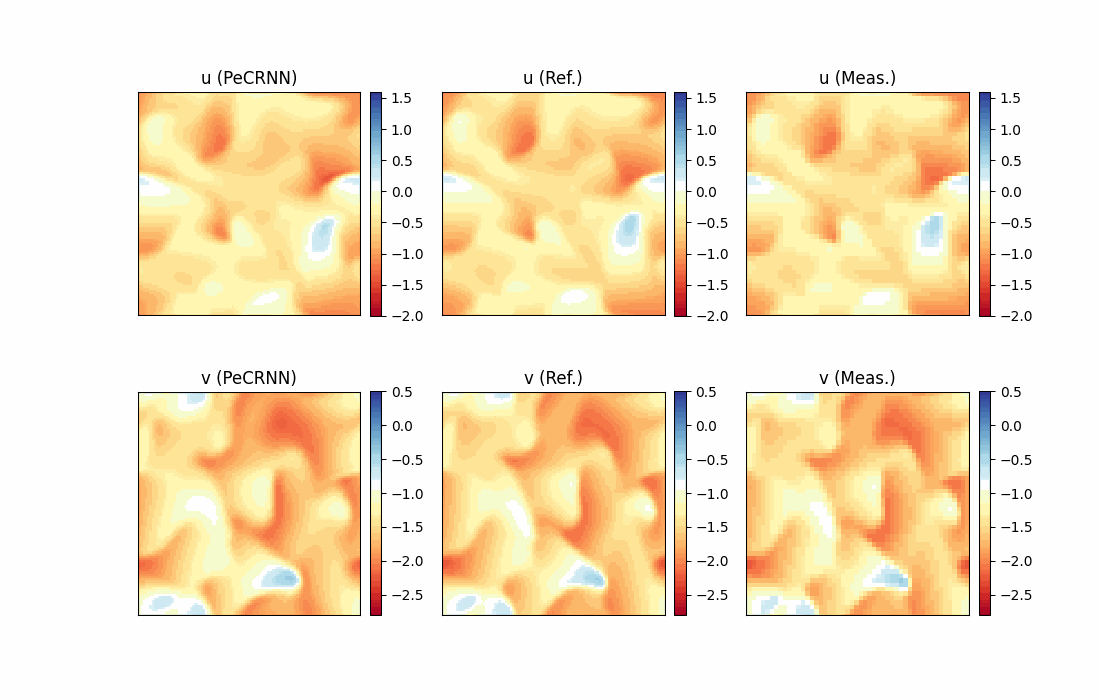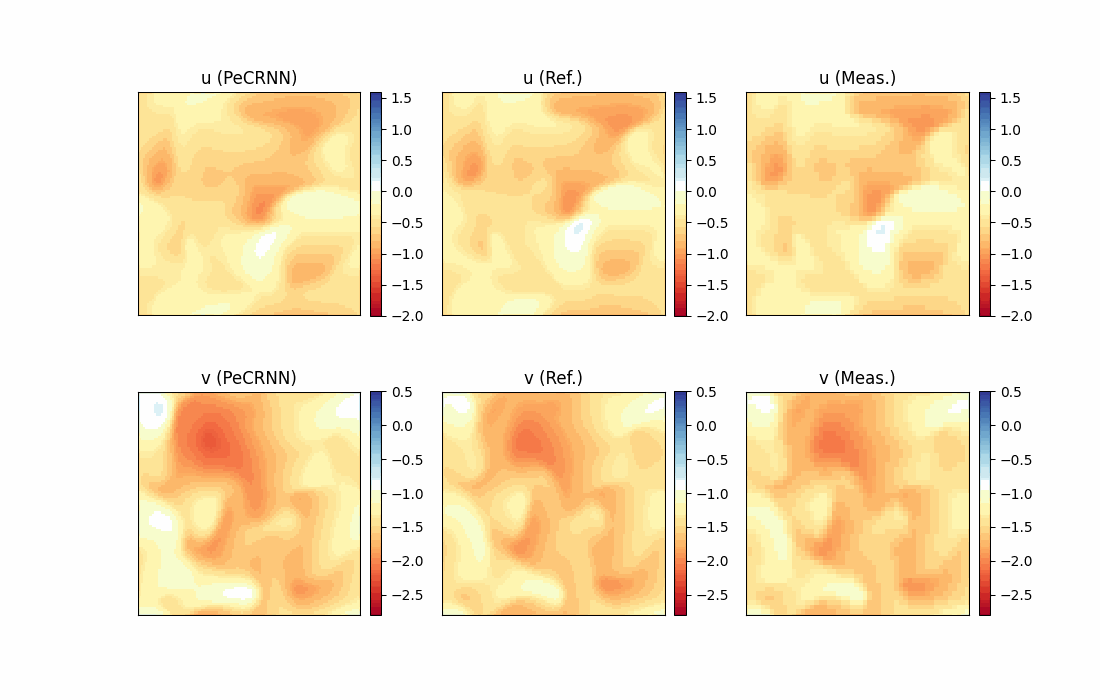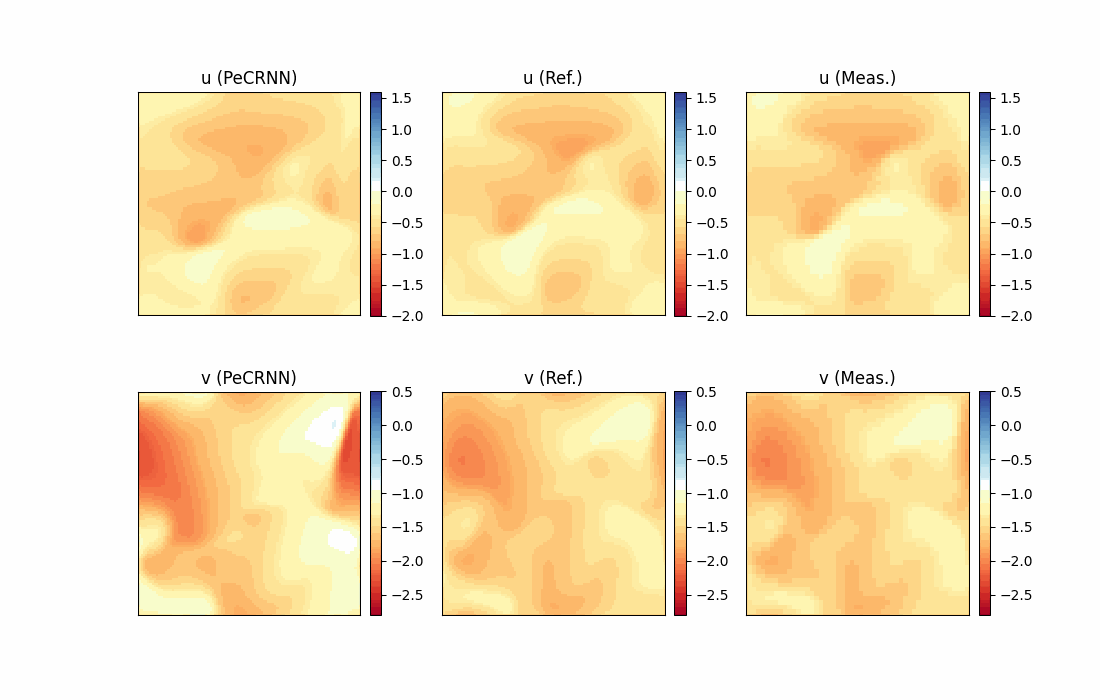
Model Evaluation and Visualization
After training, all data points in the flow field can be inferred. And related results can be visualized.