PINNs for Kovasznay Flow
Problem Description
This tutorial demonstrates how to solve the Kovasznay flow problem using Physics-Informed Neural Networks (PINNs). Kovasznay flow is an exact solution of the Navier-Stokes (N-S) equations under certain conditions. Kovasznay flow satisfies the momentum equation and continuity equation of the N-S equations, and it also satisfies Dirichlet boundary conditions.
The velocity and pressure distribution of the Kovasznay flow can be represented by the following equations:
Here, \(\lambda=\frac{1}{2\nu}-\sqrt{\frac{1}{4\nu^2}+4\pi^2}\).
We can use the Kovasznay flow as a benchmark solution to verify the accuracy and stability of the PINNs method.
Technical Pathway
The specific steps to solve this problem using MindSpore Flow are as follows:
Create the training dataset.
Build the model.
Set up the optimizer.
Define the constraints.
Train the model.
Evaluate the model.
[1]:
import time
from mindspore import context, nn, ops, jit
from mindflow import load_yaml_config
from mindflow.cell import FCSequential
from mindflow.loss import get_loss_metric
from mindspore import load_checkpoint, load_param_into_net, save_checkpoint
from src.dataset import create_dataset
context.set_context(mode=context.GRAPH_MODE, save_graphs=False, device_target="GPU")
# Load config
file_cfg = "kovasznay_cfg.yaml"
config = load_yaml_config(file_cfg)
Creating the Dataset
In this tutorial, we randomly sample the solution domain and boundary conditions to generate the training dataset and test dataset. The specific method can be found in src/dataset.py.
[2]:
ds_train = create_dataset(config)
Building the Model
In this example, we use a simple fully connected neural network with a depth of 4 layers. Each layer consists of 50 neurons, and the activation function used is tanh.
[3]:
model = FCSequential(
in_channels=config["model"]["in_channels"],
out_channels=config["model"]["out_channels"],
layers=config["model"]["layers"],
neurons=config["model"]["neurons"],
residual=config["model"]["residual"],
act="tanh",
)
[2]:
if config["load_ckpt"]:
param_dict = load_checkpoint(config["load_ckpt_path"])
load_param_into_net(model, param_dict)
params = model.trainable_params()
optimizer = nn.Adam(params, learning_rate=config["optimizer"]["initial_lr"])
Kovasznay Solver
The Kovasznay Solver consists of two parts: the Kovasznay flow equation and the boundary conditions.
The boundary conditions are set based on the reference solution mentioned above.
[4]:
import sympy
from sympy import Function, diff, symbols
from mindspore import numpy as ms_np
from mindflow import PDEWithLoss, sympy_to_mindspore
import math
class Kovasznay(PDEWithLoss):
"""Define the loss of the Kovasznay flow."""
def __init__(self, model, re=20, loss_fn=nn.MSELoss()):
"""Initialize."""
self.re = re
self.nu = 1 / self.re
self.l = 1 / (2 * self.nu) - math.sqrt(
1 / (4 * self.nu**2) + 4 * math.pi**2
)
self.x, self.y = symbols("x y")
self.u = Function("u")(self.x, self.y)
self.v = Function("v")(self.x, self.y)
self.p = Function("p")(self.x, self.y)
self.in_vars = [self.x, self.y]
self.out_vars = [self.u, self.v, self.p]
super(Kovasznay, self).__init__(model, self.in_vars, self.out_vars)
self.bc_nodes = sympy_to_mindspore(self.bc(), self.in_vars, self.out_vars)
if isinstance(loss_fn, str):
self.loss_fn = get_loss_metric(loss_fn)
else:
self.loss_fn = loss_fn
def pde(self):
"""Define the gonvering equation."""
u, v, p = self.out_vars
u_x = diff(u, self.x)
u_y = diff(u, self.y)
v_x = diff(v, self.x)
v_y = diff(v, self.y)
p_x = diff(p, self.x)
p_y = diff(p, self.y)
u_xx = diff(u_x, self.x)
u_yy = diff(u_y, self.y)
v_xx = diff(v_x, self.x)
v_yy = diff(v_y, self.y)
momentum_x = u * u_x + v * u_y + p_x - (1 / self.re) * (u_xx + u_yy)
momentum_y = u * v_x + v * v_y + p_y - (1 / self.re) * (v_xx + v_yy)
continuty = u_x + v_y
equations = {
"momentum_x": momentum_x,
"momentum_y": momentum_y,
"continuty": continuty,
}
return equations
def u_func(self):
"""Define the analytical solution."""
u = 1 - sympy.exp(self.l * self.x) * sympy.cos(2 * sympy.pi * self.y)
return u
def v_func(self):
"""Define the analytical solution."""
v = (
self.l
/ (2 * sympy.pi)
* sympy.exp(self.l * self.x)
* sympy.sin(2 * sympy.pi * self.y)
)
return v
def p_func(self):
"""Define the analytical solution."""
p = 1 / 2 * (1 - sympy.exp(2 * self.l * self.x))
return p
def bc(self):
"""Define the boundary condition."""
bc_u = self.u - self.u_func()
bc_v = self.v - self.v_func()
bc_p = self.p - self.p_func()
bcs = {"u": bc_u, "v": bc_v, "p": bc_p}
return bcs
def get_loss(self, pde_data, bc_data):
"""Define the loss function."""
pde_res = self.parse_node(self.pde_nodes, inputs=pde_data)
pde_residual = ops.Concat(axis=1)(pde_res)
pde_loss = self.loss_fn(pde_residual, ms_np.zeros_like(pde_residual))
bc_res = self.parse_node(self.bc_nodes, inputs=bc_data)
bc_residual = ops.Concat(axis=1)(bc_res)
bc_loss = self.loss_fn(bc_residual, ms_np.zeros_like(bc_residual))
return pde_loss + bc_loss
# Create the problem
problem = Kovasznay(model)
momentum_x: u(x, y)*Derivative(u(x, y), x) + v(x, y)*Derivative(u(x, y), y) + Derivative(p(x, y), x) - 0.05*Derivative(u(x, y), (x, 2)) - 0.05*Derivative(u(x, y), (y, 2))
Item numbers of current derivative formula nodes: 5
momentum_y: u(x, y)*Derivative(v(x, y), x) + v(x, y)*Derivative(v(x, y), y) + Derivative(p(x, y), y) - 0.05*Derivative(v(x, y), (x, 2)) - 0.05*Derivative(v(x, y), (y, 2))
Item numbers of current derivative formula nodes: 5
continuty: Derivative(u(x, y), x) + Derivative(v(x, y), y)
Item numbers of current derivative formula nodes: 2
u: u(x, y) - 1 + exp(-1.81009812001397*x)*cos(2*pi*y)
Item numbers of current derivative formula nodes: 3
v: v(x, y) + 0.905049060006983*exp(-1.81009812001397*x)*sin(2*pi*y)/pi
Item numbers of current derivative formula nodes: 2
p: p(x, y) - 0.5 + 0.5*exp(-3.62019624002793*x)
Item numbers of current derivative formula nodes: 3
Model Training
Using MindSpore version >= 2.0.0, we can train neural networks using the functional programming paradigm.
[6]:
def train(config):
grad_fn = ops.value_and_grad(
problem.get_loss, None, optimizer.parameters, has_aux=False
)
@jit
def train_step(pde_data, bc_data):
loss, grads = grad_fn(pde_data, bc_data)
loss = ops.depend(loss, optimizer(grads))
return loss
def train_epoch(model, dataset, i_epoch):
model.set_train()
n_step = dataset.get_dataset_size()
for i_step, (pde_data, bc_data) in enumerate(dataset):
local_time_beg = time.time()
loss = train_step(pde_data, bc_data)
if i_step % 50 == 0:
print(
"\repoch: {}, loss: {:>f}, time elapsed: {:.1f}ms [{}/{}]".format(
i_epoch,
float(loss),
(time.time() - local_time_beg) * 1000,
i_step + 1,
n_step,
)
)
for i_epoch in range(config["epochs"]):
train_epoch(model, ds_train, i_epoch)
if config["save_ckpt"]:
save_checkpoint(model, config["save_ckpt_path"])
[7]:
time_beg = time.time()
train(config)
print("End-to-End total time: {} s".format(time.time() - time_beg))
epoch: 0, loss: 0.239163, time elapsed: 12387.2ms [1/125]
epoch: 0, loss: 0.087055, time elapsed: 112.7ms [51/125]
epoch: 0, loss: 0.086475, time elapsed: 101.6ms [101/125]
epoch: 1, loss: 0.085488, time elapsed: 100.8ms [1/125]
epoch: 1, loss: 0.087387, time elapsed: 102.1ms [51/125]
epoch: 1, loss: 0.083520, time elapsed: 47.9ms [101/125]
epoch: 2, loss: 0.083846, time elapsed: 98.7ms [1/125]
epoch: 2, loss: 0.082749, time elapsed: 44.8ms [51/125]
epoch: 2, loss: 0.081391, time elapsed: 98.0ms [101/125]
epoch: 3, loss: 0.081744, time elapsed: 50.7ms [1/125]
epoch: 3, loss: 0.080608, time elapsed: 49.5ms [51/125]
epoch: 3, loss: 0.082139, time elapsed: 45.9ms [101/125]
epoch: 4, loss: 0.080847, time elapsed: 98.0ms [1/125]
epoch: 4, loss: 0.083495, time elapsed: 94.8ms [51/125]
epoch: 4, loss: 0.083020, time elapsed: 100.2ms [101/125]
epoch: 5, loss: 0.079421, time elapsed: 104.1ms [1/125]
epoch: 5, loss: 0.062890, time elapsed: 46.3ms [51/125]
epoch: 5, loss: 0.018953, time elapsed: 45.8ms [101/125]
epoch: 6, loss: 0.012071, time elapsed: 47.8ms [1/125]
epoch: 6, loss: 0.007686, time elapsed: 46.1ms [51/125]
epoch: 6, loss: 0.006134, time elapsed: 45.0ms [101/125]
epoch: 7, loss: 0.005750, time elapsed: 52.1ms [1/125]
epoch: 7, loss: 0.004908, time elapsed: 45.4ms [51/125]
epoch: 7, loss: 0.003643, time elapsed: 51.7ms [101/125]
epoch: 8, loss: 0.002799, time elapsed: 106.3ms [1/125]
epoch: 8, loss: 0.002110, time elapsed: 48.1ms [51/125]
epoch: 8, loss: 0.001503, time elapsed: 96.3ms [101/125]
epoch: 9, loss: 0.001195, time elapsed: 102.4ms [1/125]
epoch: 9, loss: 0.000700, time elapsed: 101.1ms [51/125]
epoch: 9, loss: 0.000478, time elapsed: 48.1ms [101/125]
epoch: 10, loss: 0.000392, time elapsed: 98.8ms [1/125]
epoch: 10, loss: 0.000315, time elapsed: 101.7ms [51/125]
epoch: 10, loss: 0.000236, time elapsed: 74.3ms [101/125]
epoch: 11, loss: 0.000218, time elapsed: 101.4ms [1/125]
epoch: 11, loss: 0.000184, time elapsed: 95.5ms [51/125]
epoch: 11, loss: 0.000171, time elapsed: 101.4ms [101/125]
epoch: 12, loss: 0.000145, time elapsed: 98.7ms [1/125]
epoch: 12, loss: 0.000144, time elapsed: 63.7ms [51/125]
epoch: 12, loss: 0.000126, time elapsed: 53.3ms [101/125]
epoch: 13, loss: 0.000111, time elapsed: 104.6ms [1/125]
epoch: 13, loss: 0.000109, time elapsed: 101.1ms [51/125]
epoch: 13, loss: 0.000090, time elapsed: 96.6ms [101/125]
epoch: 14, loss: 0.000094, time elapsed: 53.5ms [1/125]
epoch: 14, loss: 0.000079, time elapsed: 100.6ms [51/125]
epoch: 14, loss: 0.000070, time elapsed: 99.3ms [101/125]
epoch: 15, loss: 0.000193, time elapsed: 105.3ms [1/125]
epoch: 15, loss: 0.000066, time elapsed: 87.6ms [51/125]
epoch: 15, loss: 0.000118, time elapsed: 56.9ms [101/125]
epoch: 16, loss: 0.000074, time elapsed: 106.2ms [1/125]
epoch: 16, loss: 0.000054, time elapsed: 102.3ms [51/125]
epoch: 16, loss: 0.000065, time elapsed: 46.3ms [101/125]
epoch: 17, loss: 0.000050, time elapsed: 104.9ms [1/125]
epoch: 17, loss: 0.000056, time elapsed: 100.7ms [51/125]
epoch: 17, loss: 0.000045, time elapsed: 96.5ms [101/125]
epoch: 18, loss: 0.000043, time elapsed: 98.0ms [1/125]
epoch: 18, loss: 0.000043, time elapsed: 48.0ms [51/125]
epoch: 18, loss: 0.000050, time elapsed: 99.1ms [101/125]
epoch: 19, loss: 0.000038, time elapsed: 97.1ms [1/125]
epoch: 19, loss: 0.000051, time elapsed: 93.8ms [51/125]
epoch: 19, loss: 0.000044, time elapsed: 101.2ms [101/125]
End-to-End total time: 236.90019822120667 s
[8]:
from src import visual, calculate_l2_error
Model Prediction and Visualization
[9]:
visual(model, config, resolution=config["visual_resolution"])
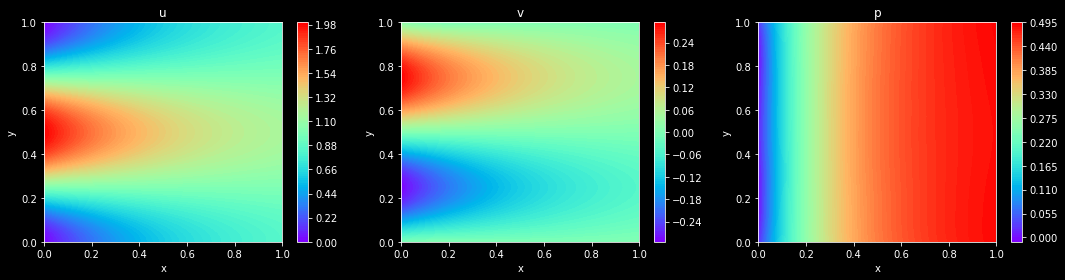
Model Evaluation
[10]:
n_samps = 10000 # Number of test samples
ds_test = create_dataset(config, n_samps)
calculate_l2_error(problem, model, ds_test)
u: 1 - exp(-1.81009812001397*x)*cos(2*pi*y)
Item numbers of current derivative formula nodes: 2
v: -0.905049060006983*exp(-1.81009812001397*x)*sin(2*pi*y)/pi
Item numbers of current derivative formula nodes: 1
p: 0.5 - 0.5*exp(-3.62019624002793*x)
Item numbers of current derivative formula nodes: 2
Relative MSE error on domain: 1.2167110294103622e-05
Relative MSE error on boundary: 4.38740462064743e-05
Relative MAE error on domain: 0.004719602203369141
Relative MAE error on boundary: 0.008604783630371093