mindspore.ops.unsorted_segment_sum
- mindspore.ops.unsorted_segment_sum(input_x, segment_ids, num_segments)[source]
Computes the sum of a tensor along segments.
Calculates a tensor such that \(\text{output}[i] = \sum_{segment\_ids[j] == i} \text{data}[j, \ldots]\), where \(j,...\) is a tuple describing the index of element in data. segment_ids selects which elements in data to sum up. Segment_ids does not need to be sorted, and it does not need to cover all values in the entire valid value range.
The following figure shows the calculation process of unsorted_segment_sum:
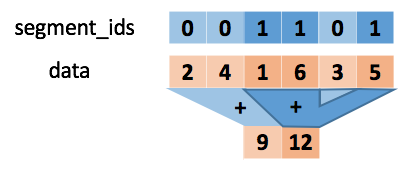
Note
If the segment_id i is absent in the segment_ids, then output[i] will be filled with 0.
On Ascend, if the value of segment_id is less than 0 or greater than the length of the input data shape, an execution error will occur.
If the sum of the given segment_ids \(i\) is empty, then \(\text{output}[i] = 0\). If the given segment_ids is negative, the value will be ignored. 'num_segments' must be equal to the number of different segment_ids.
- Parameters
input_x (Tensor) – Input Tensor contains the data to be summed. The shape is \((x_1, x_2, ..., x_R)\).
segment_ids (Tensor) – The label indicates the segment to which each element belongs. Set the shape as \((x_1, x_2, ..., x_N)\), where 0 < N <= R.
num_segments (Union[int, Tensor], optional) – Set \(z\) as num_segments, it can be an int or 0-D Tensor.
- Returns
Tensor, the shape is \((z, x_{N+1}, ..., x_R)\).
- Raises
TypeError – If num_segments is not an int or 0-D Tensor.
- Supported Platforms:
AscendGPUCPU
Examples
>>> import mindspore >>> from mindspore import Tensor >>> from mindspore import ops >>> input_x = Tensor([1, 2, 3, 4], mindspore.float32) >>> segment_ids = Tensor([0, 0, 1, 2], mindspore.int32) >>> num_segments = 4 >>> output = ops.unsorted_segment_sum(input_x, segment_ids, num_segments) >>> print(output) [3. 3. 4. 0.] >>> input_x = Tensor([1, 2, 3, 4, 2, 5], mindspore.float32) >>> segment_ids = Tensor([0, 0, 1, 2, 3, 4], mindspore.int32) >>> num_segments = 6 >>> output = ops.unsorted_segment_sum(input_x, segment_ids, num_segments) >>> print(output) [3. 3. 4. 2. 5. 0.]