Model Adversarial Attack
With continuous development and evolution of data, computing power, and theories in recent years, deep learning has been widely applied in many fields involving images, texts, voice, and autonomous driving. Meanwhile, people are getting more and more concerned about the security issues of various models in use, because AI models are vulnerable to intentional or unintentional attacks and generate incorrect results.
In this case, we will use the FGSM attack as an example to demonstrate how to attack and mislead a model.
Adversarial Example Definition
Szegedy first proposed the concept of adversarial examples in 2013.
Small perturbations that cannot be perceived by humans are added to original examples, which deteriorates the performance of deep models. Such examples are adversarial examples. For example, after a noise is added to the image that should be predicted as panda, the model predicts the image as gibbon. The example is an adversarial example.

The image comes from Explaining and Harnessing Adversarial Examples.
Attack Methods
Attacks on models can be classified from the following aspects:
Information that can be obtained by attackers:
White-box attack: Attackers have all knowledge and access permissions on a model, including the model structure, weight, input, and output. Attackers can interact with the model system in the process of generating adversarial attack data. Due to that attackers completely master information about models, they can design specific attack algorithms based on the features of the attacked model.
Black-box attack: Contrary to white-box attacks, black-box attacks only obtain limited information about models. Attackers know nothing about the structure or weight of the model and know only part of the input and output.
Attackers’ purposes:
Targeted attack: Attackers misguide the model result into a specific category.
Untargeted attacks: Attackers only want to generate incorrect results and do not care about new results.
The Fast Gradient Sign Method (FGSM) attack used in this case is a white-box attack method, which can be either a targeted or untargeted attack.
For more model security functions, see MindArmour. Currently, MindArmour supports multiple adversarial example generation methods, such as FGSM, LLC, and Substitute Attack, and provides adversarial example robustness, fuzz testing, and privacy protection and evaluation modules to enhance model security.
FGSM Attack
During the training of a classification network, a loss function is defined to measure the distance between the model output value and the actual label of the example. The model gradient is computed through backward propagation. The network parameters are updated through gradient descent to reduce the loss value and improve the model accuracy.
FGSM is a simple and efficient method for generating adversarial examples. Different from the training process of a normal classification network, FGSM computes the gradient \(\nabla_x J(\theta ,x ,y)\) of the loss to the input. The gradient indicates the sensitivity of the loss to the input change.
Then, the preceding gradient is added to the original input to increase the loss value. As a result, the classification effect of the reconstructed input examples deteriorates, and the attack is successful.
Another requirement of adversarial examples is that the difference between the generated example and the original example must be as small as possible. The sign function can be used to make the image modification as even as possible.
The generated adversarial perturbation may be expressed by using the following formula:
Adversarial examples can be formulated as follows:
In the preceding information:
\(x\): an original input image that is correctly classified as “Pandas.”
\(y\): an output of \(x\).
\(\theta\): a model parameter.
\(\varepsilon\): an attack coefficient.
\(J(\theta, x, y)\): a loss of the training network.
\(\nabla_x J(\theta)\): a backward propagation gradient.
Data Processing
In this case, MNIST is used to train LeNet with the qualified accuracy, and then the FGSM attack mentioned above is executed to deceive the network model and enable the model to implement incorrect classification.
Use the following sample code to download and decompress a dataset to a specified location.
from mindvision.dataset import Mnist
# Download and process the MNIST dataset.
download_train = Mnist(path="./mnist", split="train", shuffle=True, download=True)
download_eval = Mnist(path="./mnist", split="test", download=True)
dataset_train = download_train.run()
dataset_eval = download_eval.run()
The directory structure of the downloaded dataset files is as follows:
./mnist
├── test
│ ├── t10k-images-idx3-ubyte
│ └── t10k-labels-idx1-ubyte
└── train
├── train-images-idx3-ubyte
└── train-labels-idx1-ubyte
Training LeNet
In the experiment, LeNet is used to complete image classification. You need to define the network and use the MNIST dataset for training.
Define LeNet.
from mindvision.classification.models import lenet
network = lenet(num_classes=10, pretrained=False)
Define an optimizer and a loss function.
import mindspore.nn as nn
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')
net_opt = nn.Momentum(network.trainable_params(), learning_rate=0.01, momentum=0.9)
Define network parameters.
from mindspore.train.callback import ModelCheckpoint, CheckpointConfig
config_ck = CheckpointConfig(save_checkpoint_steps=1875, keep_checkpoint_max=10)
ckpoint = ModelCheckpoint(prefix="checkpoint_lenet", config=config_ck)
Train LeNet.
from mindspore.train import Model
from mindvision.engine.callback import LossMonitor
model = Model(network, loss_fn=net_loss, optimizer=net_opt, metrics={'accuracy'})
model.train(5, dataset_train, callbacks=[ckpoint, LossMonitor(0.01, 1875)])
Epoch:[ 0/ 5], step:[ 1875/ 1875], loss:[0.094/0.094], time:2345.947 ms, lr:0.01000
Epoch time: 3680.524 ms, per step time: 1.963 ms, avg loss: 0.094
Epoch:[ 1/ 5], step:[ 1875/ 1875], loss:[0.323/0.323], time:1250.154 ms, lr:0.01000
Epoch time: 1250.843 ms, per step time: 0.667 ms, avg loss: 0.323
Epoch:[ 2/ 5], step:[ 1875/ 1875], loss:[0.014/0.014], time:1408.945 ms, lr:0.01000
Epoch time: 1409.764 ms, per step time: 0.752 ms, avg loss: 0.014
Epoch:[ 3/ 5], step:[ 1875/ 1875], loss:[0.198/0.198], time:1332.741 ms, lr:0.01000
Epoch time: 1333.454 ms, per step time: 0.711 ms, avg loss: 0.198
Epoch:[ 4/ 5], step:[ 1875/ 1875], loss:[0.001/0.001], time:1436.917 ms, lr:0.01000
Epoch time: 1437.587 ms, per step time: 0.767 ms, avg loss: 0.001
Test the current network. You can see that LeNet has reached a high accuracy.
acc = model.eval(dataset_eval)
print("{}".format(acc))
{'accuracy': 0.9888822115384616}
Load the trained LeNet model.
import mindspore as ms
param_dict = ms.load_checkpoint("checkpoint_lenet-5_1875.ckpt")
ms.load_param_into_net(network, param_dict)
Implementing FGSM
After the accurate LeNet is obtained, the FGSM attack is used to load noise in the image and perform the test again.
Compute a backward gradient using the loss function:
class WithLossCell(nn.Cell):
"""Package a network and a loss function."""
def __init__(self, network, loss_fn):
super(WithLossCell, self).__init__()
self._network = network
self._loss_fn = loss_fn
def construct(self, data, label):
out = self._network(data)
return self._loss_fn(out, label)
class GradWrapWithLoss(nn.Cell):
"""Compute the backward gradient based on the loss."""
def __init__(self, network):
super(GradWrapWithLoss, self).__init__()
self._grad_all = ops.composite.GradOperation(get_all=True, sens_param=False)
self._network = network
def construct(self, inputs, labels):
gout = self._grad_all(self._network)(inputs, labels)
return gout[0]
Then, implement the FGSM attack according to formula (2):
import numpy as np
import mindspore as ms
class FastGradientSignMethod:
"""Implement the FGSM attack."""
def __init__(self, network, eps=0.07, loss_fn=None):
# Initialize the variables.
self._network = network
self._eps = eps
with_loss_cell = WithLossCell(self._network, loss_fn)
self._grad_all = GradWrapWithLoss(with_loss_cell)
self._grad_all.set_train()
def _gradient(self, inputs, labels):
# Compute the gradient.
out_grad = self._grad_all(inputs, labels)
gradient = out_grad.asnumpy()
gradient = np.sign(gradient)
return gradient
def generate(self, inputs, labels):
# Implement FGSM.
inputs_tensor = ms.Tensor(inputs)
labels_tensor = ms.Tensor(labels)
gradient = self._gradient(inputs_tensor, labels_tensor)
# Generate perturbations.
perturbation = self._eps*gradient
# Generate the perturbed image.
adv_x = inputs + perturbation
return adv_x
def batch_generate(self, inputs, labels, batch_size=32):
# Process the dataset.
arr_x = inputs
arr_y = labels
len_x = len(inputs)
batches = int(len_x / batch_size)
res = []
for i in range(batches):
x_batch = arr_x[i*batch_size: (i + 1)*batch_size]
y_batch = arr_y[i*batch_size: (i + 1)*batch_size]
adv_x = self.generate(x_batch, y_batch)
res.append(adv_x)
adv_x = np.concatenate(res, axis=0)
return adv_x
Process images in the test set in the MNIST dataset again.
images = []
labels = []
test_images = []
test_labels = []
predict_labels = []
ds_test = dataset_eval.create_dict_iterator(output_numpy=True)
for data in ds_test:
images = data['image'].astype(np.float32)
labels = data['label']
test_images.append(images)
test_labels.append(labels)
pred_labels = np.argmax(model.predict(ms.Tensor(images)).asnumpy(), axis=1)
predict_labels.append(pred_labels)
test_images = np.concatenate(test_images)
predict_labels = np.concatenate(predict_labels)
true_labels = np.concatenate(test_labels)
Running Attack
It can be seen from the FGSM attack formula that, the larger the attack coefficient \(\varepsilon\), the greater the change to the gradient. If the value of \(\varepsilon\) is 0, the attack effect is not reflected.
Observe the attack effect when \(\varepsilon\) is 0.
import mindspore.ops as ops
fgsm = FastGradientSignMethod(network, eps=0.0, loss_fn=net_loss)
advs = fgsm.batch_generate(test_images, true_labels, batch_size=32)
adv_predicts = model.predict(ms.Tensor(advs)).asnumpy()
adv_predicts = np.argmax(adv_predicts, axis=1)
accuracy = np.mean(np.equal(adv_predicts, true_labels))
print(accuracy)
0.9888822115384616
Set \(\varepsilon\) to 0.5 and try to run the attack.
fgsm = FastGradientSignMethod(network, eps=0.5, loss_fn=net_loss)
advs = fgsm.batch_generate(test_images, true_labels, batch_size=32)
adv_predicts = model.predict(ms.Tensor(advs)).asnumpy()
adv_predicts = np.argmax(adv_predicts, axis=1)
accuracy = np.mean(np.equal(adv_predicts, true_labels))
print(accuracy)
0.36828926282051283
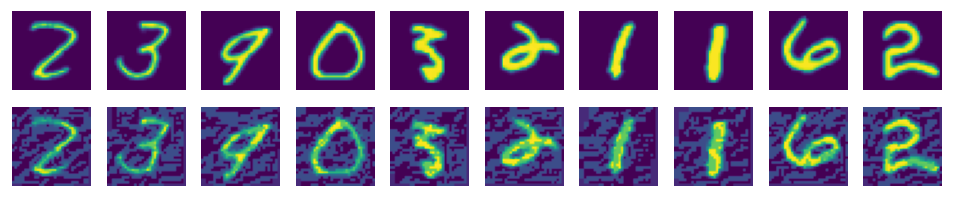
The preceding result shows that the accuracy of the LeNet model is greatly reduced.
The following shows the actual form of the attacked image. It can be seen that the image changes slightly, but the accuracy decreases greatly in the test.
import matplotlib.pyplot as plt
%matplotlib inline
adv_examples = np.transpose(advs[:10], [0, 2, 3, 1])
ori_examples = np.transpose(test_images[:10], [0, 2, 3, 1])
plt.figure(figsize=(10, 3), dpi=120)
for i in range(10):
plt.subplot(3, 10, i+1)
plt.axis("off")
plt.imshow(np.squeeze(ori_examples[i]))
plt.subplot(3, 10, i+11)
plt.axis("off")
plt.imshow(np.squeeze(adv_examples[i]))
plt.show()