Large Model Accuracy Optimization Guide

Overview and Scenarios of Accuracy Issues

Descriptions

As the Ascend AI processor (hereinafter referred to as NPU) is widely used in deep learning, the MindSpore framework, which is developed natively based on the Ascend NPU, also shows better performance advantages. During large-scale cluster training, the performance improvement will greatly save users the cost of large model development. Therefore, more and more users are gradually migrating their original training models to MindSpore. However, due to the differences in hardware and framework usage, users may encounter accuracy problems after completing the model migration.

This paper summarizes the common accuracy problems in the training process of large models and general accuracy problem localization methods, and seeks to help users quickly troubleshoot accuracy problems and shorten the time for model accuracy problem localization. When starting the work on large model accuracy optimization, you should have the basic knowledge of large model. To avoid dispersion, this document will not explain the basic concepts related to large models and focus on the introduction of accuracy optimization.

Categorized Summary of Common Problems

Various accuracy problems often occur in large model training, and the common problems include that the loss fails to converge, the loss converges poorly, the loss fails to converge at the late stage of training, the accuracy overflows, and the loss can not be fitted to the benchmark in the process of descending. There can be a variety of reasons for these accuracy problems, including the structure of the model, the dataset, the hyperparameters, the precision of the forward and reverse computation, the calculation of the optimizer, the floating-point computational accuracy, and randomness.

When accuracy problems occur, the problem can be analyzed from the reasons for these accuracy problems. A quick troubleshooting based on CheckList is performed first, followed by parameter and weight alignment, fixed randomness and turning on deterministic calculations before executing in/out problem troubleshooting and long stable training elimination. At the current stage, this paper mainly introduces the general method of accuracy localization for the scenarios with accuracy benchmarks, and the content of accuracy problem localization without accuracy benchmarks will be added successively.

Accuracy Problems Location CheckList

Before locating the operator accuracy problem, we should first eliminate the interference of other non-operator factors. Combined with the previous precision positioning cases, the CheckList before precision positioning is summarized. In order to easier locate the problems, users can first carry out quick troubleshooting according to the CheckList.

Network Structure CheckList

• Generalized structure

Key parameters	Descriptions	CheckList
num_layers	Number of transformer layers	Correspond to the Megatron num-layers parameter and check for consistency.
num_heads	Number of attention heads in transformer	Correspond to the Megatron num-attention-heads parameter and check for consistency.
hidden_size	Transformer hidden layer size	Correspond to the Megatron hidden-size parameter and check for consistency.
intermediate_size	Feed-Forward Network hidden layer size	Correspond to the Megatron ffn-hidden-size parameter and check for consistency.
n_kv_heads	Number of kv groups	Correspond to the Megatron num-query-groups parameter and check for consistency.
Regularization function	Regularization functions, common structures are LayerNorm, RMSNorm	The specified regularization function is used in MindFormers and cannot be modified by configuration. The configuration can be customized in Megatron by normalization to check for consistency.
rms_norm_eps	Regularized epsilon parameters	Correspond to the Megatron layernorm_epsilon parameter and check for consistency.
dropout	dropout in the network	Currently, when MindSpore enables dropout, recalculation cannot be enabled; if precision comparison is carried out, it is recommended that both sides be closed to reduce the random factor.
Fusion computation	Common fusion operators include FA, ROPE, Norm, SwigLU; some users will fuse Wq, Wk, Wv for computation	1. For accuracy comparison under the same hardware, if fusion algorithms are used, they should be consistent. 2. When comparing accuracy on different hardware, focus on checking whether there is any difference in the calculation of the fusion calculation part.

• MOE Structure

Key parameters	Descriptions	CheckList
expert_num	Number of experts	Correspond to the Megatron num-experts parameter and check for consistency.
num_experts_chosen	Number of experts selected per token	Correspond to the Megatron moe-router-topk parameter and check for consistency.
capacity_factor	Expert capacity factor	Correspond to the Megatron moe_expert_capacity_factor parameter and check for consistency.
aux_loss_factor	Load balancing loss contribution factor	When turned on, it is recommended to be less than 0.05. If precision alignment is performed, it is not recommended to be turned on, and is inconsistent with Megatron loss printing method.
enable_sdrop	Whether to enable the sdrop (drop implementation) method	It is recommended to set it to true; the corresponding Megatron needs to set the following parameters: moe-token-drop-policy: position moe-pad-expert-input-to-capacity: True
router_dense_type	Decide the expert sense layer	Configurable in MindFormers, FP32 calculations are recommended to prevent overflow; not configurable in Megatron.
use_fused_ops_topkrouter	Whether to use the fusion operator for dispatch as well as combine indexing calculations	Fusion operator in MindFormers takes effect when enable_sdrop=True, precision alignment is recommended to be set to True.
use_shared_expert_gating	Whether the gating factor is used in the shared expert network	Check if the network sharing expert has a gating factor, if so set it to True.

Optimizer CheckList

Key parameters	Descriptions	CheckList
adam optimizer	optimizer type	If Megatron uses the adam optimizer, the mathematically equivalent implementation of MindFormers is AdamW.
eps	adam optimizer minimal value parameter	Check the parameters for consistency, recommended value is 1e-8.
beta1	adam optimizer gradient momentum parameters	Check the parameters for consistency, recommended value is 0.9。
beta2	adam optimizer gradient variance parameter	Check the parameters for consistency, recommended value is 0.95。
weight_decay	weight decay	By default bias and one-dimensional weights are not decayed and the user is checked for special operations.
lr	learning rate	After setting up warmup, learning rate decay, draw a graph to see if the learning rate change is consistent.
lr_warmup_fraction	Learning rate warmup step percentage	After setting up warmup, learning rate decay, draw a graph to see if the learning rate change is consistent.
clip_grad	clipping gradient	Check the parameters for consistency, recommended value is 1.0.
global_batch_size	Global batch size	Consistency with the benchmark can be checked by printing a log during training.

Weight CheckList

Key parameters	Descriptions	CheckList
param_init_type	Weight initialization type	MindFormers usually sets the param_init_dtype type to FP32. This is because the gradient communication type needs to be the same as the weight type, controlling the communication type to be FP32. Megatron gradient communication type defaults to FP32 and is not tied to the weight type.
init-method-std	Distribution of weights randomly initialized	If weighted random initialization is used, parameters such as mean/std in the random distribution need to be checked for consistency.

Mixed-precision CheckList

Key parameters	Descriptions	CheckList
compute_dtype	Compute accuracy	Megatron set -bf16: true to BF16, otherwise FP16.
layernorm_compute_type	LayerNorm/RMSNorm compute precision	Megatron is not configurable, needs to check that implementations are consistent.
softmax_compute_type	When MindSpore uses FA, the internal Softmax fix is calculated with FA. Type of calculation is configurable only for small arithmetic splicing implementations	Megatron is not configurable, needs to check if the implementation is consistent.
rotary_dtype	Calculation accuracy of rotary position encoding	Megatron is not configurable, needs to check if the implementation is consistent.
Calculation of weights	accuracy calculation for each weight such as, Embedding, lm_head	Since MindFormers weight initialization needs to be set to FP32, and the usual calculation precision is BF16/FP16, it is necessary to check whether the weight data type is converted to BF16/FP16 before weight calculation.
bias add	bias in the linear layer	If bias is present, Linear layer checks consistency in the computational accuracy of add.
residual add	sum of residuals	Check that the accuracy of the calculation of the residuals is consistent with the benchmarks
loss	Loss Calculation Module	Check that the accuracy of the calculation in the entire loss module is consistent with the benchmarks
Operator High Precision Mode	Ascend Calculator supports high precision mode	Method: context.set_context(ascend_config= {"ge_options":{ "global":{ "ge.opSelectImplmode":"high_precision" } } })

Parallel Strategy CheckList

Key parameters	Descriptions	CheckList
data_parallel	data parallel	Parallel slicing affects the communication behavior, and the calculations that introduce communication after slicing may be slightly different from the single-card calculations.
model_parallel	model parallel	Parallel slicing affects the communication behavior, and the calculations that introduce communication after slicing may be slightly different from the single-card calculations.
pipeline_stage	pipeline parallel	Parallel slicing affects the communication behavior, and the calculations that introduce communication after slicing may be slightly different from the single-card calculations.
use_seq_parallel	Corresponding to Megatron Short Sequence Parallelism	Parallel slicing affects the communication behavior, and the calculations that introduce communication after slicing may be slightly different from the single-card calculations.
enable_parallel_optimizer	optimizer parallel	For optimizer parallel, MindSpore and PyTorch have different implementation schemes and inconsistent communication behavior. It is recommended to turn it off when performing precision alignment.
micro_batch_interleave_num	multicopy parallel	For optimizer parallel, MindSpore and PyTorch have different implementation schemes and inconsistent communication behavior. It is recommended to turn it off.

Other CheckList

Key parameters	CheckList
Data Check	Check if the data is abnormal, you can randomly select part of the data for decode, encode check to see if the position of input and label is correctly corresponding.
Special Words Check	Check whether the special ids such as bos_token_id, eos_token_id, pad_token_id are consistent with the ids when the data is produced.
input_ids check	Check whether inputs_id in Embedding is consistent with 0<=inputs_id<vocab_size; if there is out-of-bounds behavior, it will fetch dirty data and lead to precision anomaly.
Overflow Detection	Overflow Status Aligns PyTorch, suggest to use INFNAN_MODE, i.e., export MS_ASCEND_CHECK_OVERFLOW_MODE=INFNAN_MODE.
Graph Operator Fusion	Turn off graph operator fusion, i.e. enable_graph_kernel: False.
Training Inference Template Consistency	If training SFT, you need to make sure that the input template used for training inference is consistent.
Version Check	Check whether the versions of MindSpore, MindFormers and CANN are compatible, it is recommended to use the latest compatible version.
Differences with Open Source	MindFormers has supported the mainstream open source LLM models, and has been more fully tested. If you are developing based on the open source models in MindFormers, you can focus on checking the differences with the open source models in MindFormers.

Introduction to Accuracy Debugging Tools

In accuracy localization, MindSpore's Dump tool is mainly used. For details, please refer to Dump Function Debugging.

MindSpore's Dump tool is enabled by configuring a JSON file, which Dumps out all the operator data in the network, saving the tensor and statistics in the statistic.csv table. The following gives a JSON example of full operator Dump:

{
    "common_dump_settings": {
        "op_debug_mode": 0,
        "dump_mode": 0,
        "path": "/absolute_path",
        "net_name": "ResNet50",
        "iteration": "0|5-8|100-120",
        "saved_data": "tensor",
        "input_output": 0,
        "kernels": ["Default/Conv-op12"],
        "support_device": [0,1,2,3,4,5,6,7]
    },
    "e2e_dump_settings": {
        "enable": true,
        "trans_flag": true
    }
}

Refer to Dump Function Debug for the field meanings of the configuration parameters.

After configuring the JSON file, set the Dump environment variable to point to the configured JSON file, you need to set the absolute path:

export MINDSPORE_DUMP_CONFIG=${JSON_PATH}

After setting the environment variables, start the program training to get the corresponding Dump data.

Other Introductions

In addition to the full amount of operator Dump introduced above, the tool also supports partial data Dump, overflow Dump, specified-condition Dump and so on. Limited to space, interested users can refer to Dump function debugging for configuration and use. In addition, TroubleShooter web development debugging is also provided, can be used in the weight conversion, weight comparison and other scenarios. For more information, refer to TroubleShooter tool introduction.

Generalized Processes for Accuracy Positioning

Quickly troubleshoot the problem by using the Accuracy Problems Location CheckList section. If the accuracy problem still exists after completing the CheckList and there is no obvious direction, you can narrow down the scope of the problem by using the accuracy location generic process in this section for further troubleshooting. The current generalized process is mainly for benchmarked scenarios, and the following section will take the scenario of comparing the accuracy of GPU+PyTorch and Ascend+MindSpore as an example to introduce the accuracy localization process.

There are two main ideas for problem positioning:

• Simplified training scenarios based on single card/standalone, small-scale model replication problems.

• Fix the random factor and compare the loss difference with the benchmark during training to locate the cause of the accuracy difference.

The training process of the model can be decomposed into the following processes: data input, forward computation, loss, backward computation, gradient, optimizer weight update, and next step. The following will describe how to rank each stage of the training in conjunction with the flow of the following figure.

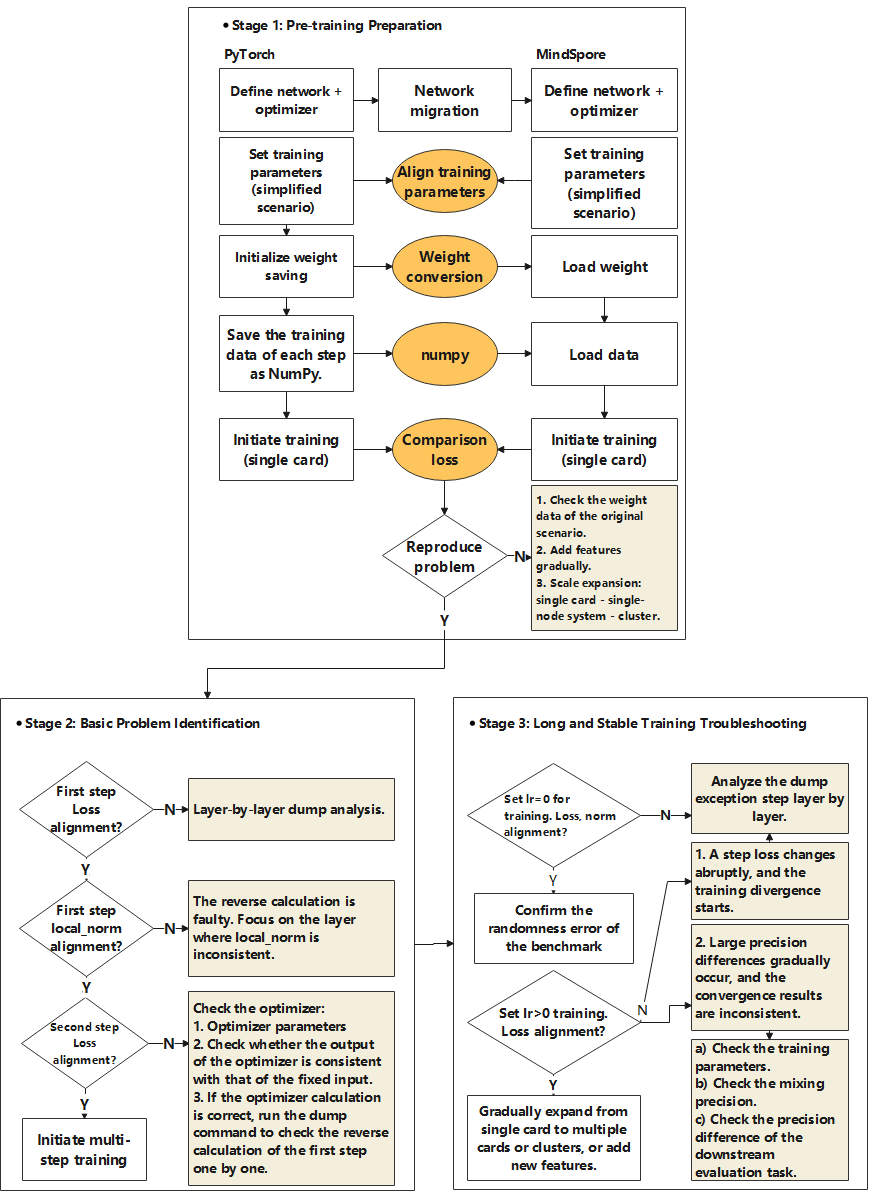
Stage 1: Pre-training Preparation

Conducting accuracy comparison between GPU+PyTorch and Ascend+MindSpore requires simplifying the scenario and fixing the randomness before reproducing the problem. There are three main parts as follows:

• Aligning parameters, downsizing models, single-card/stand-alone reproduction problems;

• Load the same weights for training;

• Each step trains the same data.

Aligning Parameters

In the parameter alignment session, the following parameters need special instructions, to ensure that PyTorch and MindSpore parameters are consistent. Parameter setting instructions:

Parameters	Suggestions	Descriptions
num_layers	2	Reduced model size facilitates quick verification that a single card can run in data-only parallelism.
learning_rate_type	constant	Fixed learning rates to ensure alignment with benchmarked learning rates.
warmup_steps	0	Steps for warmup
adam_eps	1e-8	If the user has no special requirements, follow the default settings.
dropout	0	Turn off the randomness parameter, and If there are other randomness parameters, they should be turned off.

Since features such as model parallelism, flow parallelism, sequence parallelism, optimizer parallelism increase the difficulty of precision alignment, it is recommended to turn them off first, and then gradually add parallel features after alignment.

Weight Conversion

During training, MindSpore is loaded with the same weights as PyTorch. In case of pre-training scenarios, you can use PyTorch to save an initialized weight and then convert it to MindSpore weights. Because MindSpore weight names differ from PyTorch, the essence of weight conversion is to change the names in the PyTorch weight dict to MindSpore weight names to support MindSpore loading. Refer to weight conversion guide for weight conversion.

Both MindSpore and PyTorch support bin format data, loading the same dataset for training ensures consistency from step to step.

Fixed Randomness and Start Deterministic Computation

The training process fixes randomness and turns on deterministic computation in the following way:

• NPU adds the following environment variables:

  export HCCL_DETERMINISTIC=true  # HCCL deterministic
  export ASCEND_LAUNCH_BLOCKING=1  # Hardware deterministic
  

• PyTorch code, in pretrain_gpt.py, the new seed_all method is added and called in the main method, adding the method as follows:

  import numpy as np
  import random
  
  def seed_all(seed=42):
      random.seed(seed)
      os.environ['PYTHONHASHSEED'] = str(seed)
      np.random.seed(seed)
      torch.manual_seed(seed)
      torch.use_deterministic_algorithms(True)
      torch.cuda.manual_seed_all(seed)
      torch.cuda.manual_seed(seed)
      torch.backends.cudnn.deterministic = True
      torch.backends.cudnn.enable = False
      torch.backends.cudnn.benchmark = False
  
  if __name__ == "__main__":
      seed_all()
  
      # Original code
  

• MindSpore code, in run_mindformer.py, the new seed_all method is added and called in the main method, adding the method as follows:

  import numpy as np
  import random
  
  from mindspore import context
  
  def seed_all(seed=42):
      random.seed(seed)
      os.environ['PYTHONHASHSEED'] = str(seed)
      np.random.seed(seed)
      context.set_context(deterministic="ON")
  
  def main(config):
      seed_all()
  
      # Original code
  

After completing the above preparations, single card training is initiated. If the problem is not reproduced, the scenario is expanded, such as adding relevant features, expanding the model size, etc., until the problem is reproduced, so as to locate the cause of the problem. If the problem is reproduced, or the time needed to reproduce is longer, then the problem localization in stage 2 can be opened.

Stage 2: Basic Problem Identification

By comparing the loss and local norm of the first step (step1) and the second step (step2), the forward computation, backward computation, and optimizer computation are sequentially ranked.

Comparison of Step1 Losses

After fixing the weights, dataset, and randomness, the difference in the loss value of the first step of training is compared. The loss value of the first step is obtained from the forward computation of the network. If the difference with the benchmark loss is large, it can be determined that there is an accuracy difference in the forward computation, which may be due to the model structure is not aligned, and the accuracy of the operator is abnormal. The tensor values of each layer of MindSpore and PyTorch can be obtained by printing or Dump tool. Currently, the tool does not have automatic comparison function, users need to manually identify the correspondence for comparison. For the introduction of MindSpore Dump tool, please refer to Introduction of Accuracy Debugging Tools, and for the use of PyTorch Dump tool, please refer to Function Explanation of Accuracy Tools

Find the correspondence of layers through PyTorch api_stack_dump.pkl file, and MindSpore statistic.csv file, and initially determine the degree of difference between input and output through max, min, and L2Norm. If you need further comparison, you can load the corresponding npy data for detailed comparison.

Comparison of local norm Values for step1

The local norm reflects the sum of squares of the gradients of a given weighted slice on that device, and comparing the local norm value with the benchmark allows for an initial assessment of the difference in the reverse computation. The calculation formula is as follows:

\[ localnorm = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \]

Where \(x_1 , x_2, \cdots, x_n\) is the gradient of a particular weight. MindFormers supports printing the local norm via yaml configuration as shown below:

# wrapper cell config
runner_wrapper:
  type: MFTrainOneStepCell
  local_norm: True
  scale_sense: 1
  loss_scale_value: 65536
  use_clip_grad: True

There is no configuration in Megatron to print local parameters, and you need to embedded modify the file megatron/core/optimizer/optimizer.py:

from megatron.training import get_args, print_rank_0

def get_parameters(self):
    params = []
    grad_norm_list = []
    for param_group in self.optimizer.param_groups:
        for param in param_group['params']:
            grad_norm = torch.norm(param.grad, 2)
            grad_norm_list.append(grad_norm ** 2)
            params.append(param)
    # Embedded modifications
    print_rank_0(f"print torch local norm:")
    print_rank_0(grad_norm_list)
    return params

Below is an example of a local norm comparison, comparing the local norm values corresponding to the weights.

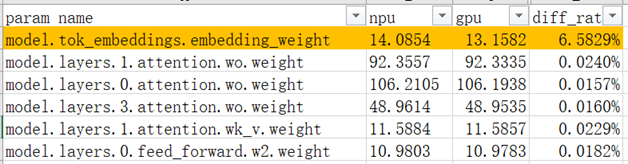
It can be found that in the scenario shown in this figure, the local norm value of model.tok_embeddings.embedding_weight has a large difference, which can be focused on troubleshooting the implementation of the Embedding and the calculation accuracy, etc.

The local norm value only serves as a preliminary judgment of whether the reverse computation is correct, if we want to compare the reverse computation in depth, we need to compare the MindSpore and PyTorch reverse computation values layer by layer by using the Dump tool.

Optimizer Computational Troubleshooting

In the case where the loss of step1 is aligned with the local norm, if the difference in the loss of step2 is large, further troubleshooting of the optimizer computation is required. The specific steps are as follows:

1. Firstly, check whether the parameters that affect the gradient update, such as checking learning rate, optimizer parameters, weight decay, are consistent with the benchmark.

2. Secondly troubleshoot the optimizer computation with the following steps:

   1. Save the gradient from PyTorch step1.

   2. Load the gradient of PyTorch at MindSpore step1 for optimizer update.

   3. Compare the difference in weights after the update or the difference in loss values at step2.

If there is a significant difference, there is a problem with the optimizer update and further targeting of the optimizer is required.

PyTorch saves the weight gradients, and to use apex as an example, modify the file apex.optimizers file.

import numpy as np

def get_parameters(self):
    params = []
    grad_id = 0
    for param_group in self.optimizer.param_groups:
        for param in param_group['params']:
            params.append(param)
            grad_id += 1
            # Embedded modification to save the gradient of torch as numpy
            np.save(f"xx/grad_{grad_id}.npy", param)
    return params

For MindFormers loading gradient, refer to mindformers/wrapper/wrapper.py implementation. Note that users need to find the correspondence between MindFormers and PyTorch gradient. Refer to the following modified code:

class MFTrainOneStepCell(nn.TrainOneStepWithLossScaleCell):
    ...
    def __init__(self):
        # Embedded modification to load the weight of torch
        grad_0 = Tensor(np.load(f"xxx/grad_1.npy"))
        grad_1 = Tensor(np.load(f"xxx/grad_x.npy"))
        ...
        self.grads = [grad_0, grad_1, ..., ]

    def construct(self, *inputs):
        ...
        # Embedded modification to force replacement of gradient with torch gradient
        grads = self.grads
        if self.use_clip_grad:
            grads, global_norm = self.clip_grad_norm(grads)

The above code, only for the realization of the reference, needs to modify the code according to the actual situation.

If you troubleshoot that there is no problem with the optimizer computation, and at the same time there is a large difference in the loss of step2, you need to re-compare the reverse computation of step1 in detail by means of Dump.

Stage 3: Long and Stable Training Troubleshooting

After the above operations of aligning the loss and local norm of step1 and step2, troubleshooting the forward computation, backward computation, and optimizer update, long stable training is initiated to compare the loss of each step.

Weights Not Updated

Set learning rate = 0, i.e., weights are not updated, and train 1k step; compare the loss values and the differences in the global norm. At the current stage, due to the large amount of data, detailed comparison of the local norm of each weight for each step is labor intensive, so the backward computation error is determined by comparing the global norm. This is a simple and quick way to verify the forward and backward computation, if there is a large difference in the value of a particular step loss or norm, then use that data alone to analyze the forward and backward. Note that global norm prints in the Megatron with the field grad norm.

Benchmark Error Confirmation

Before the training of weight update, it is necessary to confirm the benchmark error, that is, turn off the deterministic computation, repeat running the benchmark training twice to see the error of the benchmark itself, as a reference to determine whether the error is reasonable. Due to the differences in hardware or the underlying calling operator, the computational process of training will inevitably have a certain degree of error. When a loss comparison is performed between MindSpore and benchmarking model, if the error is within the benchmark error range and the error fluctuates up and down along the 0-axis, the error can be considered reasonable.

Loss Diffusion

The learning rate is set > 0, the weights are updated, and the long stability test is performed. The training to a certain step appeared the phenomenon of large differences in the loss, after which the training loss began to diverge, as shown in Fig:

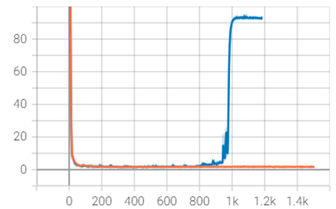
In this scenario, the training before and after the mutation can be targeted for troubleshooting, and the following troubleshooting can be tried:

• Check the data situation near the loss mutation to troubleshoot if there is any abnormal data. Decode the data to text via tokenizer to see if the data is abnormal; at the same time, you can try to skip this batch of data for training to verify whether it is caused by the data.

• Check if there is precision overflow in the vicinity of the mutation.

• You can check whether there is any abnormality in the local norm, check the training data of the Dump mutation step, troubleshoot the calculated mutation points, and analyze whether the operator outputs abnormally.

Loss Varies Greatly in the Later Stages

It is also possible to have a better fit in the early part of the training period and a large difference in the convergence loss in the later part of the training period in the long stability test, as shown in Fig:

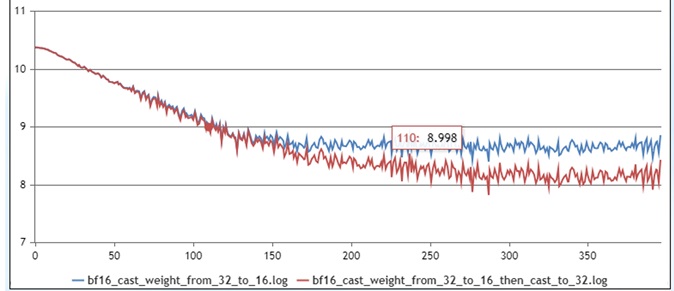
In this scenario, troubleshooting can be done from the following perspectives:

• Examine whether the parameters are aligned: focus on examining the parameters related to the optimizer, such as the optimizer type, learning rate, weight decay. We can compare whether the change of learning rate during training is consistent by drawing diagrams, and we also need to confirm whether the weight of weight decay is consistent with the benchmark.

• Mixed accuracy checking: through the Dump tool, carefully check whether the mixed accuracy is consistent with the benchmark in the calculation process;

• If there is a difference in the loss at convergence, but the difference is small, such as less than 1%, the accuracy acceptance can be performed by evaluating the downstream tasks.

Scenario Expansion

After completing the single-card alignment, gradually expand from single-card to multi-card testing and cluster testing; model size and related features such as model parallelism, flow parallelism, optimizer parallelism are added as appropriate. Gradually expand from simple scenarios to actual training scenarios, so as to troubleshoot the impact of the added features on the accuracy.

Case Details

This section will introduce the completion of accuracy ranking based on the above accuracy localization process with practical examples.

Problem Phenomenon

Training the model with a 128-card cluster and comparing training with Ascend+MindSpore training with GPU+PyTorch training reveals that the late training convergence loss is about 0.1 higher than GPU+PyTorch. As shown in the figure, the convergence is not as expected:

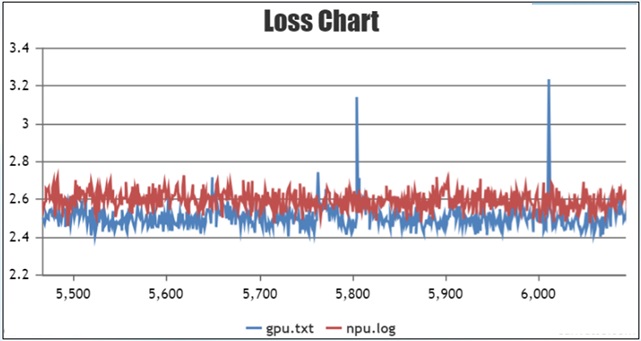
The blue line is the Ascend+MindSpore training curve and the red line is the GPU+PyTorch training curve.

Problem Location Process

Before locating the problem, check against the CheckList to confirm that there is no error and then start locating the problem.

First the loss alignment of step1 is confirmed to be OK. Comparing the local norm of step1 and calculating the difference between the local norm value of each weight and the benchmark, it is found that the local norm value of Embedding weight has a large difference with the benchmark.

The reason for this is that MindFormers uses FP32 for weight initialization, and FP32 precision is used for both forward and backward Embedding calculations, while PyTorch forward and backward calculations are bf16, which leads to differences in the calculated local norm values.

Once the computational accuracy is aligned, the exhaustive optimizer computation is also fine, and the long stable training alignment starts.

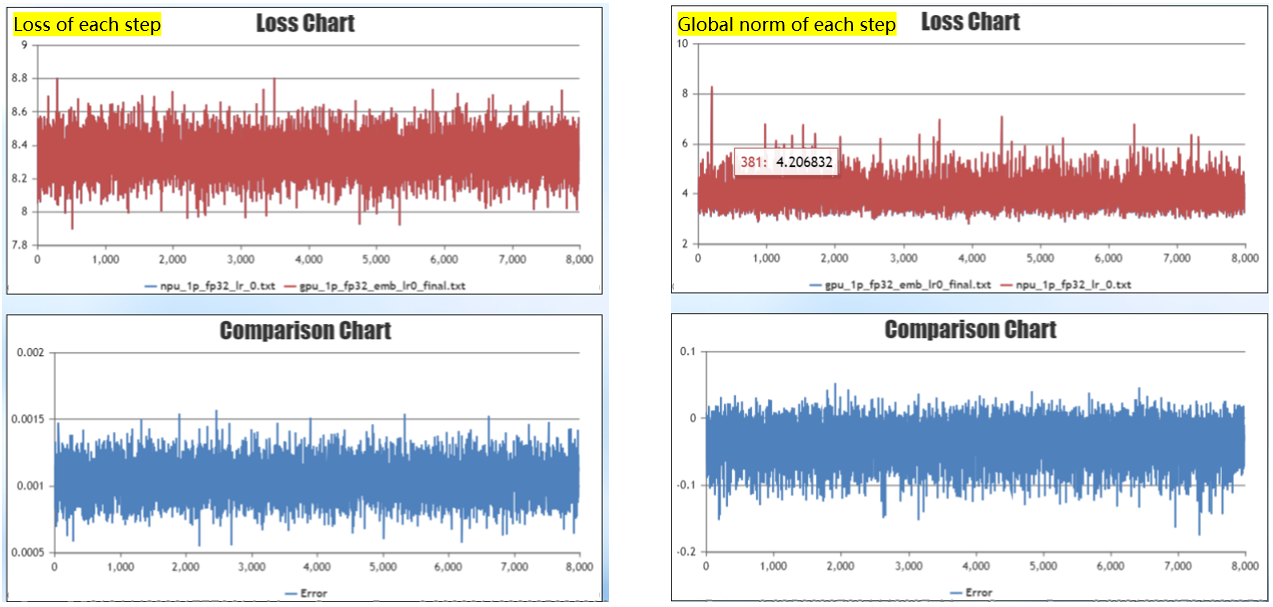
The long stable training exhaustion will be extended from single card experiments to multi-card experiments by first setting the LEARNING RATE=0, i.e., the weights are not updated. Forward computation of the loss difference of each step is around 0.001, and the forward computation error is as expected. The difference of global norm of each step is about 0.05, and the difference of reverse calculation is not significant. It is initially judged that the model migration code is correct, the model structure is consistent, and the difference of forward and reverse calculation is not significant.

Re-weight update, single card training, set learning rate=1e-5, train 1k steps. Convergence late loss has a steady 0.1 difference, reproducing the problem.

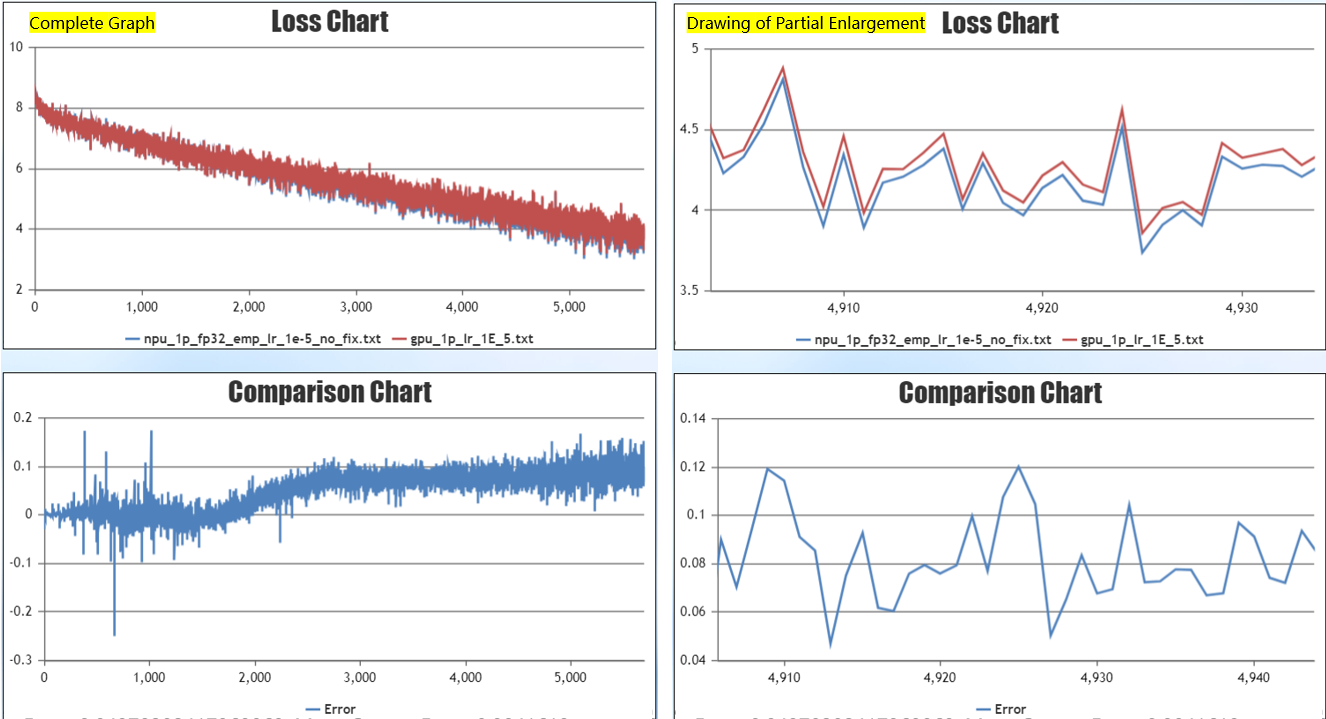
Perform problem troubleshooting. Identify the following problems:

• Identify inconsistencies in computational accuracy during training through Dump file exclusion, and harmonize inconsistencies.

• Weight decay implementation is inconsistent, weight decay is performed on all weights in user PyTorch network. bias weights and one-dimensional weights in MindFormers do not have weight decay by default.

After fixing the problem, experiment again, train 10,000 steps, the loss difference fluctuates around the 0 axis and is less than 0.03, the accuracy meets the expectation, and the single-card accuracy is aligned.

After completing the single card training, start the multi-card training test: set the learning rate=1e-5, train 1,000 steps. convergence is consistent in the late stage of training, but there is a stable 0.05 error in the middle stage of training.

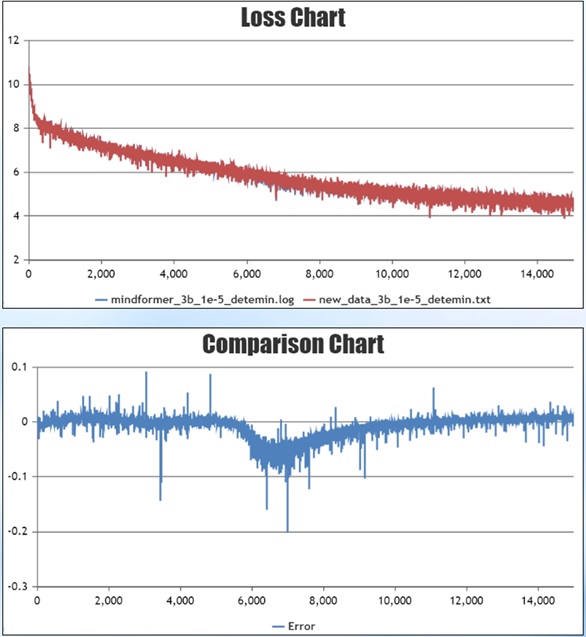
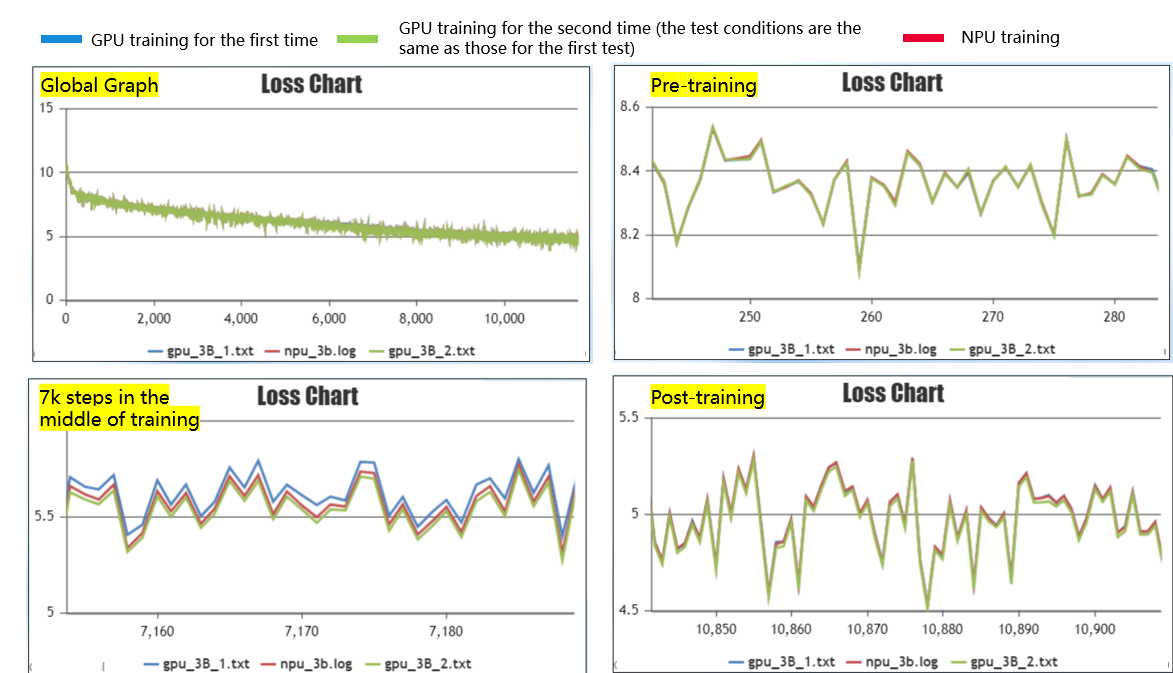
To verify that this error is within reasonable limits, the deterministic computation was turned off and the GPU experiment was run twice repeatedly. The red line in the figure is the curve of MindSpore training, and the blue and green lines are the curves of the first and second GPU training, respectively. At the training instability around 7,000 steps, the curve of MindSpore training is right between the curves of the two GPU trainings, indicating that the error is within a reasonable range and the problem is finally solved.