算子级并行
概述
随着深度学习的发展,网络模型正变得越来越大,如NLP领域已出现万亿级参数量的模型,模型容量远超单个设备的内存容量,导致单卡或数据并行均无法进行训练。
算子级并行是将网络模型中每个算子涉及到的张量进行切分,当仅切分数据维度时,为逻辑上的数据并行;当仅切分模型维度时,为逻辑上的模型并行。通过将张量切分到多个设备上,降低单个设备的内存消耗,从而使大模型的训练成为可能。
MindSpore提供两种粒度的算子级并行能力:算子级并行和高阶算子级并行。算子级并行通过简单切分策略描述张量维度分布,满足大多数场景需求。高阶算子级并行通过开放设备排布描述,支持复杂切分场景(如非连续设备分配、多维混合切分)。
目前,MindSpore支持并行的算子列表,可以参考算子级并行使用约束。
算子级并行模型支持的硬件平台包括Ascend、GPU,需要在Graph模式下运行。
相关接口:
mindspore.parallel.auto_parallel.AutoParallel(network, parallel_mode="semi_auto"):通过静态图并行封装指定并行模式,其中network是待封装的顶层Cell或函数,parallel_mode取值semi_auto,表示半自动并行模式。该接口返回封装后包含并行配置的Cell。mindspore.ops.Primitive.shard():指定算子切分策略,详细案例请参考本章的基本原理。mindspore.ops.Primitive.add_prim_attr():为满足不同场景诉求,部分算子能通过add_prim_attr接口对其分布式实现进行配置,这些配置仅对SEMI_AUTO_PARALLEL与AUTO_PARALLEL模式适用,例如:ops.Gather().add_prim_attr("manual_split", split_tuple):该接口配置Gather算子的第一个输入非均匀切分,它仅对axis=0时有效。其中split_tuple是一个元素为int类型的元组,元素之和须等于Gather算子第一个输入的第零维的长度,元组个数须等于Gather算子第一个输入的第零维切分份数。ops.Gather().add_prim_attr("primitive_target", "CPU"):该接口配置Gather算子在CPU上执行,用于异构场景。ops.Reshape().add_prim_attr("skip_redistribution"):对于ops.Reshape的前后不进行张量重排布(张量重排布见基本原理)。ops.ReduceSum().add_prim_attr("cross_batch"):该接口仅对Reduce类算子适用。当配置这个参数后,Reduce类算子如果轴被切分,则会对分片完成reduce操作后不进行多卡之间的同步,结果会和单卡不等价。ops.TensorScatterUpdate().add_prim_attr("self_define_shard", True): 对于任意打上self_define_shard标签的算子,可以支持对该算子(无论是否实现过算子切分)配置输入输出Layout。但是输入输出Layout的正确性以及算子切分后的精度需要由用户保证。
基本原理
MindSpore对每个算子独立建模,用户可以设置正向网络中每个算子的切分策略(对于未设置的算子,默认按数据并行进行切分)。
在构图阶段,框架将遍历正向图,根据算子的切分策略对每个算子及其输入张量进行切分建模,使得该算子的计算逻辑在切分前后保持数学等价。框架内部使用Tensor Layout来表达输入/输出张量在集群中的分布状态,Tensor Layout中包含了张量和设备间的映射关系,用户无需感知模型各切片在集群中如何分布,框架将自动调度分配。
此外,框架还将遍历相邻算子间张量的Tensor Layout。如果前一个算子输出张量作为下一个算子的输入张量,且前一个算子输出张量的Tensor Layout与下一个算子输入张量的Tensor Layout不同时,则需要在两个算子之间进行张量重排布(Tensor Redistribution)。对于训练网络来说,框架处理完正向算子的分布式切分之后,依靠框架的自动微分能力,即能自动完成反向算子的分布式切分。
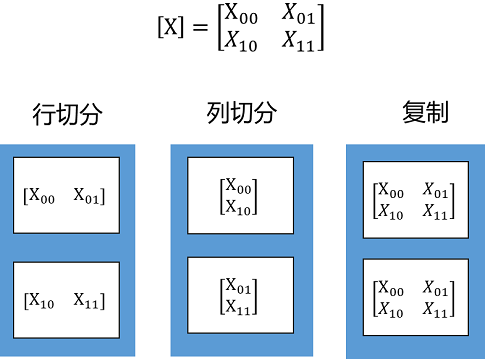
Tensor Layout用于描述Tensor在集群中的分布信息,Tensor可以按某些维度切分到集群,也可以在集群上复制。在下面这个例子中,将一个二维矩阵切分到两个节点,有三种切分方式:行切分、列切分及复制(每种切分方式即对应于一种Tensor Layout),如下图所示:
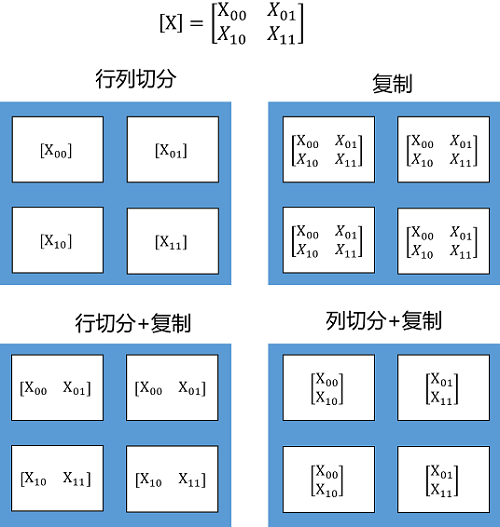
如果将二维矩阵切分到4个节点,则有四种切分方式,行列同时切分、复制、行切分+复制、列切分+复制,如下图所示:
Tensor Redistribution用于处理不同Tensor Layout之间的转换,它能在集群中将Tensor从一种排布转换成另外一种排布。所有重排布操作,都会被分解成“集合通信+split+concat”等算子组合。下面两张图说明了几种Tensor Redistribution的操作。
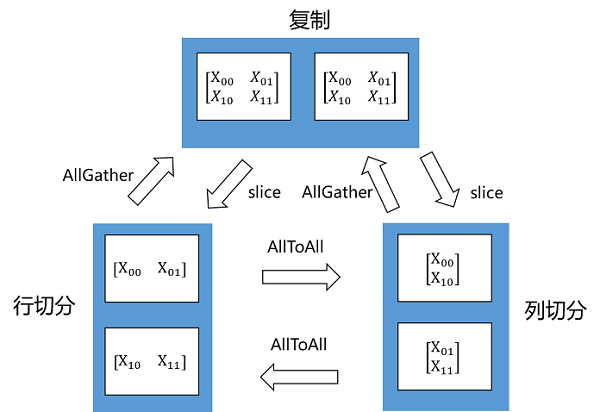
图:Tensor切分到两个节点的重排
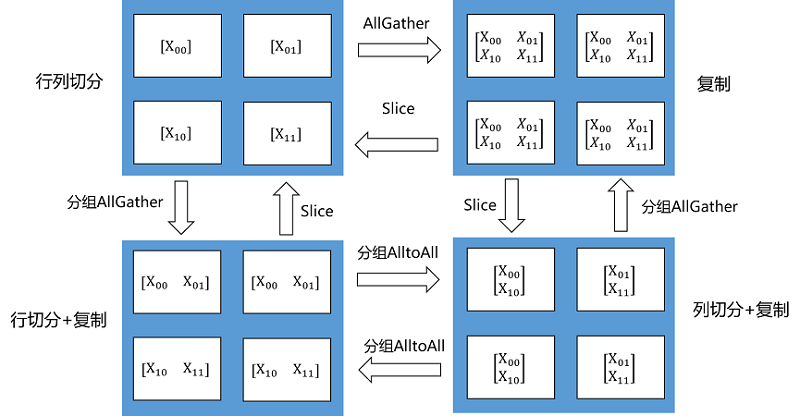
图:Tensor切分到四个节点的重排
用户可以使用shard()接口来设置算子的切分策略,该接口可以描述算子的每个输入张量的每个维度如何切分。比如MatMul().shard(((a, b), (b, c)))表示MatMul有两个输入张量,对第一个输入张量的行均匀切分a份,列均匀切分b份;对第二个输入张量的行均匀切分b份,列均匀切分c份。
import mindspore.nn as nn
from mindspore import ops
from mindspore.parallel.auto_parallel import AutoParallel
class DenseMatMulNet(nn.Cell):
def __init__(self):
super(DenseMatMulNet, self).__init__()
self.matmul1 = ops.MatMul().shard(((4, 1), (1, 1)))
self.matmul2 = ops.MatMul().shard(((1, 1), (1, 4)))
def construct(self, x, w, v):
y = self.matmul1(x, w)
z = self.matmul2(y, v)
return z
net = DenseMatMulNet()
paralell_net = AutoParallel(net, parallel_mode='semi_auto')
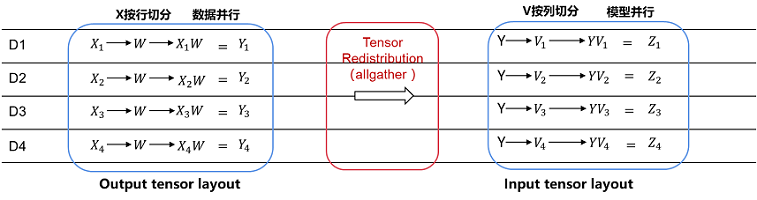
在以上例子中,用户在4个卡上计算两个连续的二维矩阵乘:Z = (X * W) * V 。第一个矩阵乘Y = X * W,用户想把X按行切4份(即数据并行);而第二个矩阵乘Z = Y * V,用户想把V按列切4份(即模型并行):
由于第一个算子输出的Tensor Layout是第零维切分到集群,而第二个算子要求第一个输入Tensor在集群上复制。所以,在图编译阶段会自动识别两个算子输出/输入之间Tensor Layout的不同,从而自动推导出Tensor重排布的算法。而这个例子所需要的Tensor重排布是一个AllGather算子(注:MindSpore的AllGather算子会自动把多个输入Tensor在第零维进行合并)
高阶算子级并行
在MindSpore中,算子级并行的配置是通过mindspore.ops.Primitive.shard()接口实现的。该接口通过tuple描述每个输入张量的切分方式,适用于大多数场景,配置过程较为简单。然而,这种切分方式仅描述了张量的切分逻辑,却隐藏了张量在设备rank上的具体排布。因此,它在表达张量切分与设备排布之间的映射关系时存在局限性,无法满足一些复杂场景的需求。
为了应对这些复杂场景,本章节将介绍一种开放设备排布描述的高阶算子级并行配置方法。
算子级并行 中介绍了MindSpore对张量的基本切分逻辑,但不能表达出所有的切分场景。例如,对于一个二维张量 "[[a0, a1, a2, a3], [a4, a5, a6, a7]]",其张量排布如下图所示:
图:二维张量排布示意
由图可知,张量的0轴,如"[a0, a1, a2, a3]"切分到了不连续的卡"[Rank0, Rank4, Rank2, Rank6]"上,而该张量按照strategy=(2, 4)切分,排布应该如下图所示:
图:二维张量按照切分策略排布示意
因此,直接对算子的输入/输出张量按照切分数目进行切分,无法表达出一些有特殊诉求的切分场景。
接口配置
为了表达出如上述场景下的切分,shard 接口进行了功能扩展。
入参in_strategy和out_strategy都额外接收新的数量类型——tuple(Layout)。其中Layout 通过设备矩阵进行初始化,并同时要求给设备矩阵的每个轴取一个别名。例如:"layout = Layout((8, 4, 4), name = ("dp", "sp", "mp"))"表示该设备共有128张卡,按照(8, 4, 4)的形状进行排列,并为每个轴分别取了别名"dp"、"sp"、"mp"。
在调用Layout时,通过传入这些轴的别名,每个张量根据其形状(shape)决定每个维度映射到设备矩阵的哪个轴,以及对应的切分份数。例如:
"dp"表示在设备排布的最高维度的8个设备内切分为8份;
"sp"表示在设备排布的中间维度的4个设备内切分为4份;
"mp"表示在设备排布的最低维度的4个设备内切分为4份。
特别地,张量的一个维度可以映射到设备的多个维度,以表达在一个维度进行多次切分。
针对上述例子中"[[a0, a1, a2, a3], [a4, a5, a6, a7]]"切分到不连续卡上的情况,可以通过如下Layout表达:
from mindspore import Layout
a = [[a0, a1, a2, a3], [a4, a5, a6, a7]]
layout = Layout((2, 2, 2), name = ("dp", "sp", "mp"))
a_strategy = layout("mp", ("sp", "dp"))
可以看到,在张量a的"[a0, a1, a2, a3]"上进行了两次切分,从而切分到了设备的"sp"与"mp"两个轴上,这样出来的结果才是:
下面,通过一个具体的例子,演示用户在8个卡上计算二维矩阵乘:Y = (X * W) 。其中,设备按照2 * 2 * 2进行组织;X的切分与上述的张量a切分一致。代码如下所示:
import mindspore.nn as nn
from mindspore import ops, Layout
from mindspore.parallel.auto_parallel import AutoParallel
class DenseMatMulNet(nn.Cell):
def __init__(self):
super(DenseMatMulNet, self).__init__()
layout = Layout((2, 2, 2), name = ("dp", "sp", "mp"))
in_strategy = (layout("mp", ("sp", "dp")), layout(("sp", "dp"), "None"))
out_strategy = (layout(("mp", "sp", "dp"), "None"), )
self.matmul1 = ops.MatMul().shard(in_strategy, out_strategy)
def construct(self, x, w):
y = self.matmul1(x, w)
return y
net = DenseMatMulNet()
paralell_net = AutoParallel(net, parallel_mode='semi_auto')