切分策略传播算法
概述
切分策略传播算法是指,用户仅需要手工定义几个关键算子的策略,计算图中其余算子的策略由算法自动生成。因为关键算子的策略已被定义,该算法的代价模型主要描述的算子之间的重排布代价(Redistribution Cost),优化目标为全图重排代价最小。因为已经定义了主要算子策略,相当于认为压缩了搜索空间,这种方案的搜索时间较短,其策略性能依赖于关键算子策略的定义,因此仍然要求用户具备一定的分析定义策略的能力。
切分策略传播算法支持的硬件平台包括Ascend、GPU,此外还同时支持PyNative模式和Graph模式。
相关接口:
mindspore.set_auto_parallel_context(parallel_mode=ParallelMode.AUTO_PARALLEL, search_mode="sharding_propagation"):设置并行模式为自动并行,且搜索模式为切分策略传播算法。mindspore.nn.Cell.shard()以及mindspore.ops.Primitive.shard():指定算子切分策略,其余算子的策略通过传播算法推导得到。目前mindspore.nn.Cell.shard()接口需要在PyNative模式下使用。
总而言之,切分策略传播算法需要用户手动配置关键算子的切分策略。
基本原理
给定计算图,切分策略传播(Sharding Propagation)使得策略由配置的算子传播到整张计算图的所有算子。在传播过程中,策略选择的目标是最小化张量重排布产生的通信代价。
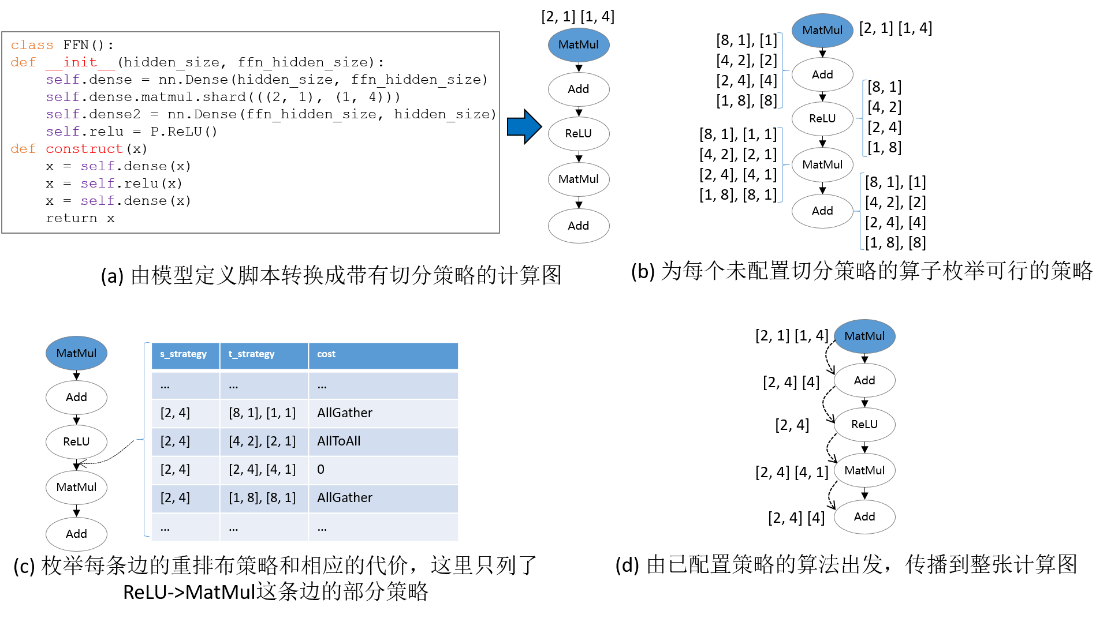
切分策略传播的输入是带有一些算子切分策略的计算图,其中的点表示算子,有向边表示数据依赖关系。切分策略传播的执行流程如下:
为未配置切分策略的算子生成可行的切分策略;
为每条边生成重排布策略及相应的代价;
从已配置切分策略的算子出发,利用广度优先搜索将切分策略传播到其它未配置切分策略的算子。传播过程的目标是最小化每条边上的重排布通信代价。若在当前传播路径上遇到已配置策略的算子,则停止传播。
下图所示的是切分策略传播的一个流程实例。在给定带有切分策略的计算图后,首先为没有配置切分策略的算子枚举其可行的策略,如下图(b)所示。然后,为每条边枚举重排布策略和相应的代价。如下图(c)所示,这里的重排布策略定义为二元组[s_strategy, t_strategy],其中s_strategy表示的是源算子(下图(c)中的ReLU)的切分策略,t_strategy表示的是目的算子(下图(c)中的MatMul)的切分策略。当沿着一条边传播到下一个算子时(如图中ReLU切分策略已确定,为[2, 4],下一步要决定MatMul算子的切分策略),总是在表中选择引起通信代价最小的目的算子的策略(即为MatMul选择[[2, 4], [4, 1]])。最后,所有算子的切分策略都被确定,如下图(d)所示。
操作实践
下面以Ascend或者GPU单机8卡为例,进行切分策略传播操作说明:
样例代码说明
下载完整的样例代码:sharding_propagation。
目录结构如下:
└─ sample_code
├─ sharding_propagation
├── train.py
└── run.sh
...
其中,train.py是定义网络结构和训练过程的脚本。run.sh是执行脚本。
配置分布式环境
通过context接口指定运行模式、运行设备、运行卡号等,与单卡脚本不同,并行脚本还需指定并行模式parallel_mode为自动并行模式,搜索模式search_mode为切分策略传播,并通过init初始化HCCL或NCCL通信。device_target会自动指定为MindSpore包对应的后端硬件设备。
import mindspore as ms
from mindspore.communication import init
ms.set_context(mode=ms.GRAPH_MODE, save_graphs=2)
ms.set_auto_parallel_context(parallel_mode=ms.ParallelMode.AUTO_PARALLEL, search_mode="sharding_propagation")
init()
ms.set_seed(1)
数据集加载
数据集加载方式与单机加载方式一致,代码如下:
import os
import mindspore.dataset as ds
def create_dataset(batch_size):
dataset_path = os.getenv("DATA_PATH")
dataset = ds.MnistDataset(dataset_path)
image_transforms = [
ds.vision.Rescale(1.0 / 255.0, 0),
ds.vision.Normalize(mean=(0.1307,), std=(0.3081,)),
ds.vision.HWC2CHW()
]
label_transform = ds.transforms.TypeCast(ms.int32)
dataset = dataset.map(image_transforms, 'image')
dataset = dataset.map(label_transform, 'label')
dataset = dataset.batch(batch_size)
return dataset
data_set = create_dataset(32)
定义网络
网络的定义以FeedForward Network(FFN)为例,与单卡网络区别在于增加了ops.MatMul()算子的切分策略:
目前Graph模式下仅支持对ops算子进行切分。
import mindspore as ms
from mindspore import nn, ops
from mindspore.common.initializer import initializer
class Dense(nn.Cell):
def __init__(self, in_channels, out_channels):
super().__init__()
self.weight = ms.Parameter(initializer("normal", [in_channels, out_channels], ms.float32))
self.bias = ms.Parameter(initializer("normal", [out_channels], ms.float32))
# matmul即为被切分的算子
self.matmul = ops.MatMul()
self.add = ops.Add()
def construct(self, x):
x = self.matmul(x, self.weight)
x = self.add(x, self.bias)
return x
class FFN(nn.Cell):
def __init__(self):
super().__init__()
self.flatten = ops.Flatten()
self.dense1 = Dense(28*28, 64)
self.relu = ops.ReLU()
self.dense2 = Dense(64, 10)
def construct(self, x):
x = self.flatten(x)
x = self.dense1(x)
x = self.relu(x)
x = self.dense2(x)
return x
net = FFN()
# 配置dense1中的matmul算子切分策略为((2, 1), (1, 4))
net.dense1.matmul.shard(((2, 1), (1, 4)))
训练网络
在这一步,我们需要定义损失函数、优化器以及训练过程,这部分与单卡写法一致:
import mindspore as ms
from mindspore import nn
optimizer = nn.Momentum(net.trainable_params(), 1e-3, 0.1)
loss_fn = nn.CrossEntropyLoss()
def forward_fn(data, target):
logits = net(data)
loss = loss_fn(logits, target)
return loss, logits
grad_fn = ms.value_and_grad(forward_fn, None, net.trainable_params(), has_aux=True)
@ms.jit
def train_step(inputs, targets):
(loss_value, _), grads = grad_fn(inputs, targets)
optimizer(grads)
return loss_value
for epoch in range(10):
i = 0
for image, label in data_set:
loss_output = train_step(image, label)
if i % 100 == 0:
print("epoch: %s, step: %s, loss is %s" % (epoch, i, loss_output))
i += 1
运行单机八卡脚本
接下来通过命令调用对应的脚本,以mpirun启动方式,8卡的分布式训练脚本为例,进行分布式训练:
bash run.sh
训练完后,日志文件保存到log_output目录下,通过在train.py中设置context: save_graphs=2,可以打印出编译过程中的IR图,其中部分文件目录结构如下:
├─ log_output
| └─ 1
| ├─ rank.0
| | └─ stdout
| ├─ rank.1
| | └─ stdout
| ...
├─ rank_0
| ├─ step_parallel_begin_xxxx.ir
| ├─ xx_validate_xxx.ir
| ...
├─ rank_1
| ├─ step_parallel_begin_xxxx.ir
| ├─ xx_validate_xxx.ir
| ...
...
关于Loss部分结果保存在log_output/1/rank.*/stdout中,示例如下:
epoch: 0, step: 0, loss is 2.3016691
epoch: 0, step: 100, loss is 2.2160375
epoch: 0, step: 200, loss is 1.7746857
epoch: 0, step: 300, loss is 1.0550221
epoch: 0, step: 400, loss is 0.763592
epoch: 0, step: 500, loss is 0.5714973
epoch: 0, step: 600, loss is 0.4949431
epoch: 0, step: 700, loss is 0.4682496
epoch: 0, step: 800, loss is 0.29194525
epoch: 0, step: 900, loss is 0.43532845
epoch: 0, step: 1000, loss is 0.46586612
...
在step_parallel_begin_xxxx.ir中,可以看到每个计算算子都被配置了切分策略:
...
%4(logits) = MatMul(%2, %3) {instance name: matmul} primitive_attrs: {input_names: [x1, x2], out_strategy: None, transpose_x2: Bool(0), transpose_b: Bool(0), in_strategy: ((2, 1), (1, 4)), output_names: [output], transpose_a: Bool(0), transpose_x1: Bool(0)} {in_strategy: ((2, 1), (1, 4))}
: (<Tensor[Float32], (256, 784)>, <Tensor[Float32], (784, 64)>) -> (<Tensor[Float32], (256, 64)>)
# Scope: (Default)
%5([CNode]1647) = Load($(@1_train_step.1349:para4_dense1.bias), %para16_u)
: (<Ref[Tensor[Float32]], (64), ref_key=:dense1.bias>, <UMonad, NoShape>) -> (<Tensor[Float32], (64)>)
# Scope: (Default)
%6(logits) = Add(%4, %5) {instance name: add} primitive_attrs: {output_names: [output], input_names: [x, y]} {in_strategy: ((2, 4), (4))}
: (<Tensor[Float32], (256, 64)>, <Tensor[Float32], (64)>) -> (<Tensor[Float32], (256, 64)>)
# Scope: (Default)
%7(logits) = ReLU(%6) {instance name: relu} primitive_attrs: {output_names: [output], input_names: [x]} {in_strategy: ((2, 4))}
: (<Tensor[Float32], (256, 64)>) -> (<Tensor[Float32], (256, 64)>)
# Scope: (Default)
%8([CNode]1641) = Load($(@1_train_step.1349:para5_dense2.weight), %para16_u)
: (<Ref[Tensor[Float32]], (64, 10), ref_key=:dense2.weight>, <UMonad, NoShape>) -> (<Tensor[Float32], (64, 10)>)
# Scope: (Default)
%9(logits) = MatMul(%7, %8) {instance name: matmul} primitive_attrs: {output_names: [output], transpose_a: Bool(0), input_names: [x1, x2], transpose_x2: Bool(0), transpose_x1: Bool(0), transpose_b: Bool(0)} {in_strategy: ((2, 4), (4, 1))}
: (<Tensor[Float32], (256, 64)>, <Tensor[Float32], (64, 10)>) -> (<Tensor[Float32], (256, 10)>)
# Scope: (Default)
...
例如对于上面的第一个MatMul算子,输入的策略in_strategy已被配置为((2, 1), (1, 4)),Add算子的切分策略被配置为((2, 4), (4))。
(<Tensor[Float32], (256, 784)>, <Tensor[Float32], (784, 64)>) -> (<Tensor[Float32], (256, 64)>)
代表算子的原输入,对于第一个MatMul算子,第一、第二个输入的shape分别为(256, 784)、(784, 64),输出的shape为(256, 64)。
在xx_validate_xxx.ir中,可以看到各个算子的输入输出张量是已经被切分后的:
...
%3(equiv[CNode]4) = MatMul(%1, %2) {instance name: matmul} primitive_attrs: {input_names: [x1, x2], out_strategy: None, transpose_x2: Bool(0), transpose_b: Bool(0), in_strategy: ((2, 1), (1, 4)), output_names: [output], transpose_a: Bool(0), transpose_x1: Bool(0)} cnode_attrs: {related_comm_node_id: "30707"} cnode_primal_attrs: {unique_id: "31021", related_fusion_key: "all_reduce_2-511848487187618470_1", related_node_id: "28192"} {in_strategy: ((2, 1), (1, 4))}
: (<Tensor[Float32], (128, 784)>, <Tensor[Float32], (784, 16)>) -> (<Tensor[Float32], (128, 16)>)
# Scope: (Default)
# In file train.py:40/ x = self.matmul(x, self.weight)/
%4(equiv[CNode]1647) = Load(%para4_dense1.bias, U) cnode_primal_attrs: {unique_id: "31025"}
: (<Ref[Tensor[Float32]], (16), ref_key=:dense1.bias>, <UMonad, NoShape>) -> (<Tensor[Float32], (16)>)
# Scope: (Default)
%5(equiv[CNode]4) = Add(%3, %4) primitive_attrs: {output_names: [output], input_names: [x, y]} cnode_attrs: {related_comm_node_id: "30709"} cnode_primal_attrs: {unique_id: "31020", related_fusion_key: "all_reduce_2-511848487187618470_1", related_node_id: "28190"} {in_strategy: ((2, 4), (4))}
: (<Tensor[Float32], (128, 16)>, <Tensor[Float32], (16)>) -> (<Tensor[Float32], (128, 16)>)
# Scope: (Default)
# In file train.py:41/ x = self.add(x, self.bias)/
%6(equiv[CNode]4) = ReLU(%5) {instance name: relu} primitive_attrs: {output_names: [output], input_names: [x]} cnode_primal_attrs: {unique_id: "31008"} {in_strategy: ((2, 4))}
: (<Tensor[Float32], (128, 16)>) -> (<Tensor[Float32], (128, 16)>)
# Scope: (Default)
# In file train.py:58/ x = self.relu(x)/
%7(equiv[CNode]1641) = Load(%para5_dense2.weight, U) cnode_primal_attrs: {unique_id: "31018"}
: (<Ref[Tensor[Float32]], (16, 10), ref_key=:dense2.weight>, <UMonad, NoShape>) -> (<Tensor[Float32], (16, 10)>)
# Scope: (Default)
%8(equiv[CNode]4) = MatMul(%6, %7) {instance name: matmul} primitive_attrs: {output_names: [output], transpose_a: Bool(0), input_names: [x1, x2], transpose_x2: Bool(0), transpose_x1: Bool(0), transpose_b: Bool(0)} cnode_attrs: {related_comm_node_id: "30724"} cnode_primal_attrs: {unique_id: "31015", related_fusion_key: "all_reduce_2-511848487187618470_1", related_node_id: "28180"} {in_strategy: ((2, 4), (4, 1))}
: (<Tensor[Float32], (128, 16)>, <Tensor[Float32], (16, 10)>) -> (<Tensor[Float32], (128, 10)>)
# Scope: (Default)
# In file train.py:40/ x = self.matmul(x, self.weight)/
...
对于第一个MatMul算子,其输入根据策略((2, 1), (1, 4))切分后,第一、第二个输入的shape分别从原来的(256, 784)、(784, 64)切分为(128, 784)、(784, 16),因此得到输出的shape为(128, 16)。
其他启动方式如动态组网、rank table的启动可参考启动方式。
配置算子切分策略的经验性原则
给定一个新模型,从用户的角度,关键问题是配置哪些算子的切分策略来获得较好的性能。由于策略传播的目标是最小化张量重排布的代价,而非最小化端到端的迭代时间,因此,为“关键算子”配置合适的切分策略是十分重要的。然而,并不存在明确的规定约束哪些算子是必须配置切分策略的。尽管如此,基于我们训练大模型的经验,确实有一些原则可以用来指导新用户配置并行策略。我们总结出3条经验性的原则供参考,详见切分技巧。