实现区域海洋模型GOMO
概述
GOMO(Generalized Operator Modelling of the Ocean)是基于 OpenArray 的三维区域海洋模型,由清华大学黄小猛老师开发的用于海洋建模和并行计算的通用模型(Xiaomeng Huang et al, 2019)。GOMO模型中的基本方程和实现算法来自于POM2k模型(Blumberg and Mellor, 1987)。三维海洋模型在地球系统模式中有重要的作用,以质量能量守恒定律为约束,通过模拟海洋洋流、漩涡等现象,不仅能够很好的表示海面温度和海表面高度的分布,还能够实时的预测台风、海啸等现象。传统的海洋模型代码实现复杂,且都是基于CPU运行,我们使用MindSpore对GOMO模型进行框架加速,结合GPU,能获得较大的性能提升。
本篇教程将主要介绍如何在GPU上,使用MindSpore构建并运行三维海洋模型GOMO。
示例代码目录结构如下:
└── ocean_model
├── README.md # descriptions about ocean model GOMO
├── scripts
│ ├── run_distribute_train.sh # launch distributed training for GPU
├──src
│ ├── GOMO.py # GOMO model
│ ├── Grid.py # grid initial
│ ├── stencil.py # averaging and differential stencil oprator
│ ├── op_operator.py # averaging and differential kernel operator
│ ├── read_var.py # read variables from nc file
├── train.py # train script
整体执行流程如下:
准备海洋模拟数据集Seamount文件,加载处理数据;
定义GOMO变量初始化;
定义GOMO模型;
加载数据集并进行训练,训练完成后,查看结果及保存文件。
准备环节
安装软件依赖
安装MindSpore
实践前,确保已经正确安装MindSpore。如果没有,可以通过MindSpore安装页面安装。
安装netCDF4
pip install netCDF4
准备数据
本教程使用的是netCDF格式的Seamount文件,贝克曼和海德沃格尔提出的Seamount问题是区域海洋模型广泛使用的理想试验案例(Beckmann and Haidvogel, 1993)。
加载数据
加载Seamount数据文件,从文件脚本中读取变量的初始化值,Seamount文件中的数据类型是双精度Float64,需要将其转成Float32进入MindSpore计算。加载处理数据的脚本在源码的src/read_var.py脚本中。
import numpy as np
import netCDF4 as nc
# variable name list
params_name = ['z', 'zz', 'dz', 'dzz', 'dx', 'dy', 'cor', 'h', 'fsm', 'dum', 'dvm', 'art', 'aru', 'arv', 'rfe', 'rfw',
'rfn', 'rfs', 'east_e', 'north_e', 'east_c', 'north_c', 'east_u', 'north_u', 'east_v', 'north_v', 'tb',
'sb', 'tclim', 'sclim', 'rot', 'vfluxf', 'wusurf', 'wvsurf', 'e_atmos', 'ub', 'vb', 'uab', 'vab', 'elb',
'etb', 'dt', 'uabw', 'uabe', 'vabs', 'vabn', 'els', 'eln', 'ele', 'elw', 'ssurf', 'tsurf', 'tbe', 'sbe',
'sbw', 'tbw', 'tbn', 'tbs', 'sbn', 'sbs', 'wtsurf', 'swrad']
def load_var(file_obj, name):
"""load variable from nc data file"""
data = file_obj.variables[name]
data = data[:]
data = np.float32(np.transpose(data, (2, 1, 0)))
return data
def read_nc(file_path):
""" put the load variable into the dict """
variable = {}
file_obj = nc.Dataset(file_path)
for name in params_name:
variable[name] = load_var(file_obj, name)
return variable
定义GOMO网络
GOMO模型基于动量、能量和质量守恒定律,推导微分方程组和边界条件,确定需要求解的7个方程组,详细的公式推导参考论文。图1是GOMO的整体执行流程图。
首先,从Seamount数据中加载数据,用于模型中变量的初始化。加载初始值和模型参数后,计算分为内模态循环和外模态循环两个部分。在外模态循环中,主要计算二维海表面高度el和二维平均风速ua、va。在内模态循环中,循环次数iend是训练的总时间步数(由用户输入设定),内模态循环的计算三维数组占主导地位,依次计算湍流动能q2和产生湍流动能的湍流长度q2l、温度t和盐度s、x和y方向的风速u和v。计算完成之后,保存所需的变量结果,结束训练。
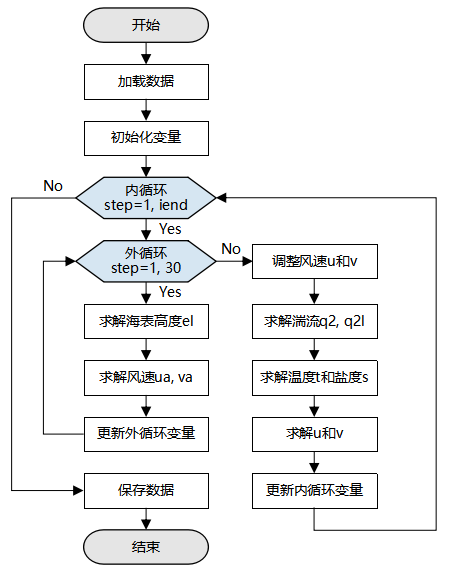
图1:GOMO模型流程图
初始化变量
...
from src.GOMO import GOMO_init
...
if __name__ == "__main__":
...
# define grid and init variable update
net_init = GOMO_init(im, jm, kb, stencil_width)
...
定义GOMO模型
def construct(self, etf, ua, uab, va, vab, el, elb, d, u, v, w, kq, km, kh, q2, q2l, tb, t, sb, s,
rho, wubot, wvbot, ub, vb, egb, etb, dt, dhb, utb, vtb, vfluxb, et):
"""construct"""
x_d, y_d, z_d = self.x_d, self.y_d, self.z_d
q2b, q2lb = self.q2b, self.q2lb
dx, dy = self.dx, self.dy
# surface forcing
w = w * (1 - self.z_h) + self.z_h * self.vfluxf
# lateral_viscosity
advx, advy, drhox, drhoy, aam = self.lateral_viscosity(dx, dy, u, v, dt, self.aam, ub, vb, x_d, y_d, z_d, rho, self.rmean)
# mode_interaction
adx2d, ady2d, drx2d, dry2d, aam2d, advua, advva, egf, utf, vtf = self.mode_interaction(advx, advy, drhox, drhoy, aam, x_d, y_d, d, uab, vab, ua, va, el)
# ===========external model===========
vamax = 0
elf = 0
for iext in range(1, 31):
# external_el
elf = self.external_el(x_d, y_d, d, ua, va, elb)
# external_ua
advua, uaf = self.external_ua(iext, x_d, y_d, elf, d, ua, va, uab, vab, el, elb, advua, aam2d, adx2d, drx2d, wubot)
# external_va
advva, vaf = self.external_va(iext, x_d, y_d, elf, d, ua, va, uab, vab, el, elb, advva, aam2d, ady2d, dry2d, wvbot)
# external_update
etf, uab, ua, vab, va, elb, el, d, egf, utf, vtf, vamax = self.external_update(iext, etf, ua, uab, va, vab, el, elb, elf, uaf, vaf, egf, utf, vtf, d)
# ===========internal model===========
if self.global_step != 0:
# adjust_uv
u, v = self.adjust_uv(u, v, utb, vtb, utf, vtf, dt)
# internal_w
w = self.internal_w(x_d, y_d, dt, u, v, etf, etb, vfluxb)
# internal_q
dhf, a, c, gg, ee, kq, km, kh, q2b_, q2, q2lb_, q2l = self.internal_q(x_d, y_d, z_d, etf, aam, q2b, q2lb, q2, q2l, kq, km, kh, u, v, w, dt, dhb, rho, wubot, wvbot, t, s)
q2b = ops.Assign()(self.q2b, q2b_)
q2lb = ops.Assign()(self.q2lb, q2lb_)
# internal_t_t
a, c, ee, gg, tb, t = self.internal_t_(t, tb, self.wtsurf, self.tsurf, self.swrad, self.tclim, self.tbe, self.tbw, self.tbn, self.tbs, x_d, y_d, z_d, dt, u, aam, self.h, self.dum, v, self.dvm, w, dhf, etf, a, kh, self.dzz, c, self.dzz1, ee, gg, dx, self.dz, dy, self.fsm, dhb)
# internal_t_s
a, c, ee, gg, sb, s = self.internal_t_(s, sb, self.wssurf, self.ssurf, self.swrad0, self.sclim, self.sbe, self.sbw, self.sbn, self.sbs, x_d, y_d, z_d, dt, u, aam, self.h, self.dum, v, self.dvm, w, dhf, etf, a, kh, self.dzz, c, self.dzz1, ee, gg, dx, self.dz, dy, self.fsm, dhb)
# dense
rho = self.dens(s, t, self.zz, self.h, self.fsm)
# internal_u
uf, a, c, gg, ee, wubot = self.internal_u(x_d, z_d, dhf, u, v, w, ub, vb, egf, egb, ee, gg, self.cbc, km, advx, drhox, dt, dhb)
# internal_v
vf, a, c, gg, ee, wvbot = self.internal_v(y_d, z_d, dhf, u, v, w, ub, vb, egf, egb, ee, gg, self.cbc, km, advy, drhoy, dt, dhb)
# adjust_ufvf
u, v, ub, vb = self.adjust_ufvf(u, v, uf, vf, ub, vb)
# internal_update
egb, etb, dt, dhb, utb, vtb, vfluxb, et = self.internal_update(egf, etb, utf, vtf, etf, et)
steps = ops.AssignAdd()(self.global_step, 1)
return elf, etf, ua, uab, va, vab, el, elb, d, u, v, w, kq, km, kh, q2, q2l, tb, t, sb, s, rho, wubot, wvbot, \
ub, vb, egb, etb, dt, dhb, utb, vtb, vfluxb, et, steps, vamax, q2b, q2lb
在__main__函数中调用定义好的GOMO模型:
...
from src.GOMO import GOMO
...
if __name__ == "__main__":
...
# define GOMO model
Model = GOMO(im=im, jm=jm, kb=kb, stencil_width=stencil_width, variable=variable, x_d=x_d, y_d=y_d, z_d=z_d,
q2b=q2b, q2lb=q2lb, aam=aam, cbc=cbc, rmean=rmean)
...
训练网络
运行脚本
训练脚本定义完成之后,调用scripts目录下的shell脚本,启动训练进程。
使用以下命令运行脚本:
sh run_distribute_train.sh <im> <jm> <kb> <step> <DATASET_PATH>
脚本需要传入变量im、jm、kb、step、DATASET_PATH,其中:
im,jm,kb:模拟的海洋区域分辨率,与使用的数据相关;step:训练的时间步数(与图1中的iend对应);DATASET_PATH:训练数据路径。
训练完后,训练过程中变量的变化值保存在train/outputs目录下,每隔5个时间步保存一次数据,主要保存了4个变量值,分别是东向的风速、北向的风速(单位是m/s),位温度(单位是K),海表面高度(单位是m)。
└─outputs
├─u_5.npy
├─v_5.npy
├─t_5.npy
├─et_5.npy
├─u_10.npy
├─v_10.npy
├─t_10.npy
├─et_10.npy
其中,
*.npy:指保存的变量。文件名称具体含义:变量名称_step数.npy。
引用
Huang X, Huang X, Wang D, et al. OpenArray v1. 0: a simple operator library for the decoupling of ocean modeling and parallel computing[J]. Geoscientific Model Development, 2019, 12(11).
Blumberg A F, Mellor G L. A description of a three‐dimensional coastal ocean circulation model[J]. Three‐dimensional coastal ocean models, 1987, 4: 1-16.
Beckmann A, Haidvogel D B. Numerical simulation of flow around a tall isolated seamount. Part I: Problem formulation and model accuracy[J]. Journal of Physical Oceanography, 1993, 23(8): 1736-1753.
