量子神经网络初体验
量子神经网络的结构
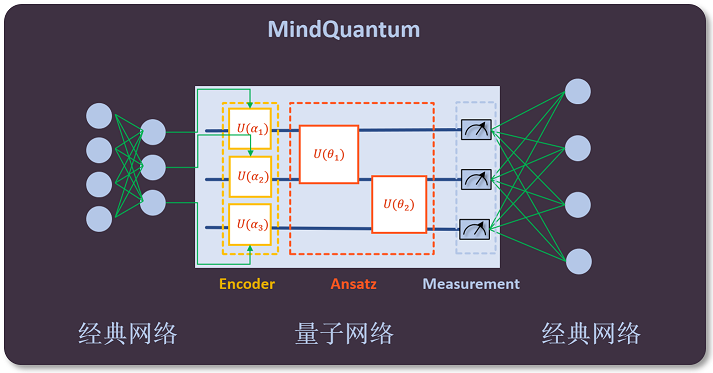
在MindQuantum中,量子神经网络(Quantum Neural Network, QNN)的结构如下图所示,其通常由三部分构成:
(1)一个(或多个)编码线路,用于将经典数据编码到量子数据(通常称为Encoder);
(2)一个(或多个)训练线路,用于训练带参量子门中的参数(通常称为Ansatz);
(3)一个(或多个)测量,用于检测测量值(例如在Z方向上测量,就是某个量子比特的量子态在Z轴上的投影,该测量得到的是量子态关于泡利Z算符(不限定于泡利Z算符,换成其它的算符亦可)的期望值)是否接近于目标期望值。
下面,我们通过一个简单的例子来体验一下如何使用MindQuantum。
简单的例子

我们搭建如上图所示的量子神经网络,其中Encoder由一个H门,1个RX门、1个RY门和1个RZ门构成,Ansatz由1个RX门和1个RY门构成,测量则是作用在第0位量子比特上的泡利Z算符。
问题描述:我们将Encoder看成是系统对初始量子态的误差影响(参数\(\alpha_0, \alpha_1\)和\(\alpha_2\)是将原经典数据经过预处理(可选)后得到的某个固定值,即为已知值,在此分别设为0.2, 0.3和0.4)。我们需要训练一个Ansatz来抵消掉这个误差,使得最后的量子态还是处于\(|0\rangle\)态。
思路:对末态执行泡利Z算符测量,此时的测量值就是此时的量子态关于泡利Z算符的期望值。由于\(|0\rangle\)是算符Z的本征态,且本征值为1,容易知道
也就是说,目标期望值为1。可以通过测量得到的期望值来验证此时的状态是否为\(|0\rangle\)。
解决方案:通过训练Ansatz中的参数,希望测量值接近于目标期望值,换句话说,我们只需让测量值尽可能接近于\(|0\rangle\)态关于泡利Z算符对应的期望值,那么此时的状态就是\(|0\rangle\),即Ansatz抵消了Encoder对初始量子态产生的误差。
环境准备
导入本教程所依赖的模块
[1]:
import numpy as np # 导入numpy库并简写为np
from mindquantum.core.circuit import Circuit # 导入Circuit模块,用于搭建量子线路
from mindquantum.core.gates import H, RX, RY, RZ # 导入量子门H, RX, RY, RZ
搭建Encoder
根据图示的量子线路图,我们可以在MindQuantum中搭建Encoder。
[2]:
# pylint: disable=W0104
encoder = Circuit() # 初始化量子线路
encoder += H.on(0) # H门作用在第0位量子比特
encoder += RX(f'alpha{0}').on(0) # RX(alpha_0)门作用在第0位量子比特
encoder += RY(f'alpha{1}').on(0) # RY(alpha_1)门作用在第0位量子比特
encoder += RZ(f'alpha{2}').on(0) # RZ(alpha_2)门作用在第0位量子比特
encoder = encoder.no_grad() # Encoder作为整个量子神经网络的第一层,不用对编码线路中的梯度求导数,因此加入no_grad()
encoder.as_encoder() # 将量子线路设置为encoder线路
encoder.summary() # 总结Encoder
encoder.svg()
==================Circuit Summary==================
|Total number of gates : 4. |
|Parameter gates : 3. |
|with 3 parameters are : alpha0, alpha1, alpha2. |
|Number qubit of circuit: 1 |
===================================================
[2]:
从对Encoder的Summary中可以看到,该量子线路由4个量子门组成,其中有3个含参量子门且参数为\(\alpha_0,\alpha_1,\alpha_2\),该量子线路调控的量子比特数为1。
然后,我们需要对Encoder中的参数进行赋值。由于Encoder中的参数\(\alpha_0, \alpha_1\)和\(\alpha_2\)分别为已知值0.2, 0.3和0.4,因此可以直接对参数进行赋值,并打印此时的状态。
[3]:
alpha0, alpha1, alpha2 = 0.2, 0.3, 0.4 # alpha0, alpha1, alpha2为已知的固定值,分别赋值0.2, 0.3 和0.4
state = encoder.get_qs(pr={'alpha0': alpha0, 'alpha1': alpha1, 'alpha2': alpha2}, ket=True)
print(state)
(0.5669903122552596-0.1753906567580312j)¦0⟩
(0.800814626197614+0.08034947292077024j)¦1⟩
上述步骤为了展示MindQuantum可以演化量子线路(若量子线路中的量子门带参数,则需要对参数赋值)并得到演化后的末态。从上述打印可以看到,演化后得到的末态为\(|0\rangle\)和\(|1\rangle\)组成的叠加态,各项对应的振幅为上述打印的状态左边对应的数值。
说明:
(1)通过调用量子线路的get_qs函数,我们能够得到该量子线路在全零态基础上演化出来的量子态。
(2)get_qs的pr参数代表变分量子线路中的参数值,ket表示是否将量子态输出为右矢形式。
搭建Ansatz
同样地,我们也可以在MindQuantum中搭建Ansatz。
[4]:
# pylint: disable=W0104
ansatz = Circuit() # 初始化量子线路
ansatz += RX(f'theta{0}').on(0) # RX(theta_0)门作用在第0位量子比特
ansatz += RY(f'theta{1}').on(0) # RY(theta_1)门作用在第0位量子比特
ansatz.as_ansatz() # 将量子线路设置成待训练线路
ansatz.svg() # 打印量子线路
[4]:
从对Ansatz的Summary中可以看到,该量子线路由2个量子门组成,其中有2个含参量子门且参数为\(\theta_0, \theta_1\),该量子线路调控的量子比特数为1。
然后,对Ansatz中的参数进行赋值。由于Ansatz为需要训练的量子线路,因此Ansatz中的参数\(\theta_0\)和\(\theta_1\)可以随机设定,通常默认设为初始值0。我们同样可以打印此时的量子态,不过这并不是必要的步骤,只是为了再次熟悉一下get_qs函数。
[5]:
theta0, theta1 = 0, 0 # 对theta0, theta1进行赋值,设为初始值0, 0
state = ansatz.get_qs(pr=dict(zip(ansatz.params_name, [theta0, theta1])), ket=True)
print(state)
1¦0⟩
从上述打印可以看到,此时的状态为\(|0\rangle\)且振幅为1。这是因为对于Ansatz来说,默认的输入量子态为\(|0\rangle\),而且其中的参数\(\theta_0\)和\(\theta_1\)都为0,此时的RX(0)门和RY(0)门都相当于I门,因此整个线路演化的过程就是\(|0\rangle\)经过\(I\cdot I\),那么最后输出的态当然就是\(|0\rangle\)了。
那么完整的量子线路就是Encoder加上Ansatz。
[6]:
# pylint: disable=W0104
circuit = encoder.as_encoder() + ansatz.as_ansatz() # 完整的量子线路由Encoder和Ansatz组成
circuit.svg()
[6]:
从对完整的量子线路的Summary中可以看到,该量子线路由6个量子门组成,其中有5个含参量子门且参数为\(\alpha_0,\alpha_1,\alpha_2,\theta_0,\theta_1\),该量子线路调控的量子比特数为1。
构建哈密顿量
我们对第0位量子比特执行泡利Z算符测量,构建对应的哈密顿量。
[7]:
from mindquantum.core.operators import QubitOperator # 导入QubitOperator模块,用于构造泡利算符
from mindquantum.core.operators import Hamiltonian # 导入Hamiltonian模块,用于构建哈密顿量
ham = Hamiltonian(QubitOperator('Z0', -1)) # 对第0位量子比特执行泡利Z算符测量,且将系数设置为-1,构建对应的哈密顿量
print(ham)
-1 [Z0]
从上述打印可以看到,此时构建的哈密顿量为对第0位量子比特执行泡利Z算符测量,且系数为-1。之所以将系数设为-1,是因为在量子神经网络的训练中,Ansatz中的参数的梯度会一直下降,同时测量值也会一直减少。如果最后收敛于-1,那么此时对应的量子态是\(|1\rangle\)而不是\(|0\rangle\),如下所示
而我们所希望得到的是\(|0\rangle\)态。所以,将系数设为-1,那么当测量值为-1时,此时对应的量子态就是\(|0\rangle\)态,如下所示
说明:
(1)QubitOperator是作用于量子比特的算子的总和,主要用于构造泡利算符;一般格式如下:QubitOperator(term=None, coefficient=1.0);
(2)Hamiltonian是哈密顿量包装器,主要用于构建哈密顿量,一般格式如下:Hamiltonian(QubitOperator(‘X0 Y2’, 0.5)),X0和Y2表示泡利X算符作用在第0位量子比特,泡利Y算符作用在第2位量子比特,系数为0.5。
生成变分量子线路模拟算子
对于上述搭建的量子线路,我们可以在MindQuantum生成一个变分量子线路模拟算子对其进行模拟。
首先,为了方便,我们对Encoder和Ansatz中的参数数组分别命名为encoder_names和ansatz_names。
[8]:
encoder_names = encoder.params_name # Encoder中所有参数组成的数组,encoder.para_name系统会自动生成
ansatz_names = ansatz.params_name # Ansatz中所有参数组成的数组,ansatz.para_name系统会自动生成
print('encoder_names = ', encoder.params_name, '\nansatz_names =', ansatz.params_name)
encoder_names = ['alpha0', 'alpha1', 'alpha2']
ansatz_names = ['theta0', 'theta1']
从上述打印可以看到,encoder_names为Encoder中所有参数\(\alpha_0, \alpha_1, \alpha_2\)组成的数组,ansatz_names为Ansatz中所有参数\(\theta_0,\theta_1\)组成的数组,这两个数组会在生成变分量子线路模拟算子时用到。
然后,我们通过Simulator模块得到变分量子线路演化和梯度求解的算子。
[9]:
# 导入Simulator模块
from mindquantum.simulator import Simulator
# 生成一个基于mqvector后端的模拟器,并设置模拟器的比特数为量子线路的比特数。
sim = Simulator('mqvector', circuit.n_qubits)
# 获取模拟器基于当前量子态的量子线路演化以及期望、梯度求解算子
grad_ops = sim.get_expectation_with_grad(ham,
circuit)
# Encoder中的alpha0, alpha1, alpha2这三个参数组成的数组,
# 将其数据类型转换为float32,并储存在encoder_data中。
# MindQuantum支持多样本的batch训练,Encoder数组是两个维度,
# 第一个维度为样本,第二个维度为特征(即参数)
encoder_data = np.array([[alpha0, alpha1, alpha2]]).astype(np.float32)
# Ansatz中的theta0, theta1这两个参数组成的数组,将其数据类型转换为float32,
# 并储存在ansatzr_data中,Ansatz数据只有一个维度,特征(即参数)
ansatz_data = np.array([theta0, theta1]).astype(np.float32)
# 根据Encoder和Ansatz的数据,输出变分量子线路的测量值,Encoder中的参数的导数和Ansatz中的参数的导数
measure_result, encoder_grad, ansatz_grad = grad_ops(encoder_data, ansatz_data)
print('Measurement result: ', measure_result)
print('Gradient of encoder parameters: ', encoder_grad)
print('Gradient of ansatz parameters: ', ansatz_grad)
Measurement result: [[0.29552022+0.j]]
Gradient of encoder parameters: [[[0.+0.j 0.+0.j 0.+0.j]]]
Gradient of ansatz parameters: [[[-0.37202556+0.j 0.87992317+0.j]]]
从上述打印可以看到,测量结果(期望值)为0.29552022,Encoder中的3个参数的导数为0,0,0(因为我们对Encoder设置了no_grad()),Ansatz中的2个参数的导数为-0.37202555,-0.87992316。
这里通过get_expectation_with_grad产生的只是一个算子,还不能进行训练,要把它放到量子神经网络里面才能进行训练。通过训练Ansatz中的参数,可以使得Ansatz中的参数的导数一直下降并接近于0,那么测量值也就会接近于-1。
说明:
(1)Simulator的get_expectation_with_grad用于生成变分量子线路来模拟算子,一般格式如下:
Simulator.get_expectation_with_grad(ham,
circ_right,
circ_left,
parallel_worker=1)
此函数适用于计算如下模型:
其中circ_right是\(U_r\),circ_left是\(U_l\),当不提供时,默认跟circ_right是相同的线路,parallel_worker指定并行数,当需要编码的经典数据是一个batch时,合理设置此参数可以提高计算效率。
(2)MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景覆盖三大目标,提供支持异构加速的张量可微编程能力,支持云、服务器、边和端多种硬件平台。
搭建量子神经网络
[10]:
# pylint: disable=W0104
from mindquantum.framework import MQLayer # 导入MQLayer
import mindspore as ms # 导入mindspore
ms.set_seed(1) # 设置生成随机数的种子
ms.set_context(mode=ms.PYNATIVE_MODE, device_target="CPU")
QuantumNet = MQLayer(grad_ops)
QuantumNet
[10]:
MQLayer<
(evolution): MQOps<1 qubit mqvector VQA Operator>
>
上述打印可以看到,我们已经成功搭建了量子机器学习层,其可以无缝地跟MindSpore中其它的算子构成一张更大的机器学习网络。
说明:
(1)MindQuantum中的量子线路梯度计算算子都是在PYNATIVE_MODE下的,因此需要设置MindSpore的运行模式。
(2)我们也可以通过如下代码方式搭建量子机器学习层,只是在MindQuantum中,已经将下述过程封装打包,这样我们就可以直接利用MQLayer模块搭建量子机器学习层。对于更复杂的量子-经典混合神经网络,如下搭建方式会展示它的优势。
from mindspore import nn
class MQLayer(nn.Cell):
def __init__(self, expectation_with_grad, weight='normal'):
super(MQLayer, self).__init__()
self.evolution = MQOps(expectation_with_grad)
weight_size = len(
self.evolution.expectation_with_grad.ansatz_params_name)
self.weight = Parameter(initializer(weight,
weight_size,
dtype=ms.float32),
name='ansatz_weight')
def construct(self, x):
return self.evolution(x, self.weight)
训练
我们采用Adam优化器优化Ansatz中的参数。
[11]:
from mindspore.nn import Adam, TrainOneStepCell # 导入Adam模块和TrainOneStepCell模块
opti = Adam(QuantumNet.trainable_params(), learning_rate=0.5) # 需要优化的是Quantumnet中可训练的参数,学习率设为0.5
net = TrainOneStepCell(QuantumNet, opti)
for i in range(200):
res = net(ms.Tensor(encoder_data))
if i % 10 == 0:
print(i, ': ', res)
0 : [[0.2837115]]
10 : [[-0.8851233]]
20 : [[-0.97001773]]
30 : [[-0.9929431]]
40 : [[-0.9939507]]
50 : [[-0.9967015]]
60 : [[-0.99878186]]
70 : [[-0.9995535]]
80 : [[-0.9999011]]
90 : [[-0.99998033]]
100 : [[-0.9999989]]
110 : [[-0.99999785]]
120 : [[-0.999997]]
130 : [[-0.9999987]]
140 : [[-0.9999998]]
150 : [[-1.]]
160 : [[-0.99999994]]
170 : [[-1.]]
180 : [[-1.]]
190 : [[-1.]]
从上述打印可以看到,最后测量值收敛于-1。
说明:
(1)Adam模块通过自适应矩估计算法更新梯度,可以优化Ansazt中的参数,输入的是神经网络中可训练的参数;一般格式如下:nn.Adam(net.trainable_params(), learning_rate=0.5);
(2)TrainOneStepCell模块为网络训练包类,用优化器包装网络。生成的单元格使用输入“inputs”进行训练,将在构造函数中创建反向图,以更新参数,有不同的并行模式可用于训练。一般格式如下:nn.TrainOneStepCell(network, optimizer, sens=1.0)。
结果呈现
由于测量值已经收敛于-1,所以我们可以打印此时Ansatz中的参数。
[12]:
theta0, theta1 = QuantumNet.weight.asnumpy()
print(QuantumNet.weight.asnumpy())
[ 2.2420275 -1.0756909]
从上述打印可以看到,此时Ansatz中的参数\(\theta_1, \theta_2\)分别为2.2420275和-1.0756909。
通过get_qs,可以输出量子线路在最优参数时的量子态。
[13]:
pr = {'alpha0': alpha0, 'alpha1': alpha1, 'alpha2': alpha2, 'theta0': theta0, 'theta1': theta1}
state = circuit.get_qs(pr=pr, ket=True)
print(state)
(0.37129760050057437-0.9285139157007681j)¦0⟩
(1.4564552975271372e-05+6.455516706194153e-07j)¦1⟩
从上述打印可以看到,这就是量子线路在最优参数时的量子态。从其数值表示可以看到,这是一个接近于目标态\(|0\rangle\)的态。最后,我们计算一下此量子态与目标态\(|0\rangle\)的保真度(用于验证两个量子态的相似程度),并将保真度打印。
[14]:
state = circuit.get_qs(pr=pr)
fid = np.abs(np.vdot(state, [1, 0]))**2 # 保真度fidelity为向量内积的绝对值的模平方,即计算此时量子态对应的向量与|0>态对应的向量[1,0]的内积的模平方
print(fid)
0.9999999997874573
可以看到,此时的保真度为100.00%,也就是说,该状态与目标态\(|0\rangle\)的相似程度为100.00%。
综上所述,我们搭建了一个简单的量子神经网络,通过训练Ansatz中的参数,抵消了Encoder对初始量子态产生的误差,使得最后的量子态仍为\(|0\rangle\),且保真度达到100.00%。
至此,我们通过MindQuantum完成了对量子神经网络的初体验!赶紧动手体验一下量子编程的乐趣吧!
若想查询更多关于MindQuantum的API,请点击:https://mindspore.cn/mindquantum/。



