Reading IR

Overview

When a model compiled using MindSpore runs in the graph mode set_context(mode=GRAPH_MODE) and set_context(save_graphs=True) is set in the configuration, some intermediate files will be generated during graph compliation. These intermediate files are called IR files. Currently, there are three IR files:

.ir file: An IR file that describes the model structure in text format and can be directly viewed using any text editors.
.dat file: An IR file that describes the model structure more strictly than the .ir file. It contains more contents and can be directly viewed using any text editors.
.dot file: An IR file that describes the topology relationships between different nodes. You can use this file by graphviz as the input to generate images for users to view the model structure. For models with multiple operators, it is recommended using the visualization component MindInsight to visualize computing graphs.

Saving IR

set_context(save_graphs=True) is used to save the intermediate code in each compilation phase. The intermediate code can be saved in two formats. One is the text format with the suffix .ir, and the other is the graphical format with the suffix .dot. When the network scale is small, you are advised to use the graphical format that is more intuitive. When the network scale is large, you are advised to use the text format that is more efficient.

You can run the graphviz command to convert a .dot file to the picture format. For example, you can run the dot -Tpng *.dot -o *.png command to convert a .dot file to a .png file.

In the training script train.py, we add the following code to the set_context function, when running the training script, MindSpore will automatically store the IR file generated during compilation to the specified path.

if __name__ == "__main__":
    set_context(save_graphs=True, save_graphs_path="path/to/ir/files")

After the training command is executed, several files were generated under the specified path.

.
├──00_parse_0000.ir
├──00_parse_0001.dat
├──00_parse_0002.dot
├──01_symbol_resolve_0003.ir
├──01_symbol_resolve_0004.dat
├──01_symbol_resolve_0005.dot
├──02_combine_like_graphs_0006.ir
├──02_combine_like_graphs_0007.dat
├──02_combine_like_graphs_0008.dot
├──03_inference_opt_prepare_0009.ir
├──03_inference_opt_prepare_0010.dat
├──03_inference_opt_prepare_0011.dot
├──04_abstract_specialize_0012.ir
├──04_abstract_specialize_0013.dat
├──04_abstract_specialize_0014.dot
...

The IR files starting with digits and underscores are generated during the ME graph compilation. The compute graph is saved in each phase of the pipeline. Let’s see the important phases.

The parse phase parses the entrance function and this phase generates MindIR initially. If viewing the IR file, we can see that only the graph information of the top Cell is parsed in this phase.
The symbol_resolve phase recursively parses entrance function, mainly recursive resolution entry functions directly or indirectly reference to other functions and objects. When using the unsupported syntax, it will get an error in this phase.
The abstract_specialize phase means that the data type and shape information for all nodes in the IR is deduced from the input information. When you want to know the shape or data type of a specific operator in IR, you can view this IR file.
The optimize phase refers hardware-independent optimization is performed. The automatic differential and automatic parallel functions are also performed. This stage can be subdivided into several substages. In the list of IR files, where the files prefixed with opt_pass_ [ordinal] are IR files saved after the end of these sub-stages, non-framework developers do not need to pay too much attention.
The validate phase will verify the compiled compute graph and check the temporary operators which should be removed in the prior phase. If any temporary operator exists, the process will report an error and exit.
The task_emit phase will transfer the compute graph to the backend for further processing.
The execute phase will execute the compute graph. The IR graph in this stage is the final graph in the phase of frontend.

In addition, because the backend is closer to the bottom layer, non-framework developers do not need to pay much attention to other IR files saved during the backend optimization process (such as files that begin with hwopt). Non-framework developers only need to look at the file named graph_build_[Graph Sequence Number]_[IR File Sequence Number].ir, i.e. IR after all front and back end optimizations.

Multiple files may be saved because the backend is optimized on subgraphs, which is different from the mechanism by which multiple subgraphs on the front end are saved in the same file.

IR File Contents Introduction

The following is an example to describe the contents of the IR file. Run the script:

import mindspore as ms
from mindspore import nn, ops

ms.set_context(mode=ms.GRAPH_MODE)
ms.set_context(save_graphs=True, save_graphs_path="./")

class Net(nn.Cell):
    def __init__(self):
        super().__init__()
        self.add = ops.Add()
        self.sub = ops.Sub()
        self.mul = ops.Mul()
        self.div = ops.Div()

    def func(x, y):
        return self.div(x, y)

    def construct(self, x, y):
        a = self.sub(x, 1)
        b = self.add(a, y)
        c = self.mul(b, self.func(a, b))
        return c

input1 = ms.Tensor(3, ms.float32)
input2 = ms.Tensor(2, ms.float32)
net = Net()
out = net(input1, input2)
print(out)

ir Introduction

Use a text editing software (for example, vi) to open the 04_abstract_specialize_0012.ir file output after execution. The file contents are as follows (Here is MindSpore 1.6, and the content may have some imperceptible changes with the version upgrade):

#IR entry      : @1_construct_wrapper.21
#attrs         :
#Total params  : 2
  4
%para1_x : <Tensor[Float32]x()>
%para2_y : <Tensor[Float32]x()>
  7
#Total subgraph : 3
  9
subgraph attr:
Undeterminate : 0
subgraph @2_construct.22(%para3_x, %para4_y) {
 %0(a) = Sub(%para3_x, Tensor(shape=[], dtype=Float32, value= 1)) {instance name: sub} primitive_attrs: {input_names: [x, y], output_names: [output]}
     : (<Tensor[Float32]x()>, <Tensor[Float32]x()>) -> (<Tensor[Float32]x()>)
     # In file train.py(34)/        a = self.sub(x, 1)/
 %1(b) = Add(%0, %para4_y) {instance name: add} primitive_attrs: {input_names: [x, y], output_names: [output]}
     : (<Tensor[Float32]x()>, <Tensor[Float32]x()>) -> (<Tensor[Float32]x()>)
     # In file train.py(35)/        b = self.add(a, y)/
 %2([CNode]5) = call @3_func.23(%0, %1)
     : (<Tensor[Float32]x()>, <Tensor[Float32]x()>) -> (<Tensor[Float32]x()>)
     # In file train.py(36)/        c = self.mul(b, self.func(a, b))/
 %3(c) = Mul(%1, %2) {instance name: mul} primitive_attrs: {input_names: [x, y], output_names: [output]}
     : (<Tensor[Float32]x()>, <Tensor[Float32]x()>) -> (<Tensor[Float32]x()>)
     # In file train.py(36)/        c = self.mul(b, self.func(a, b))/
 Return(%3)
     : (<Tensor[Float32]x()>)
     # In file train.py(37)/        return c/
}
 29
subgraph attr:
Undeterminate : 0
subgraph @3_func.23(%para5_x, %para6_y) {
 %0([CNode]20) = Div(%para5_x, %para6_y) {instance name: div} primitive_attrs: {input_names: [x, y], output_names: [output]}
     : (<Tensor[Float32]x()>, <Tensor[Float32]x()>) -> (<Tensor[Float32]x()>)
     # In file train.py(31)/        return self.div(x, y)/
 Return(%0)
     : (<Tensor[Float32]x()>)
     # In file train.py(31)/        return self.div(x, y)/
}
 40
subgraph attr:
subgraph @1_construct_wrapper.21() {
 %0([CNode]2) = call @2_construct.22(%para1_x, %para2_y)
     : (<Tensor[Float32]x()>, <Tensor[Float32]x()>) -> (<Tensor[Float32]x()>)
     # In file train.py(37)/        return c/
 Return(%0)
     : (<Tensor[Float32]x()>)
     # In file train.py(37)/        return c/
}

The above contents can be divided into two parts. The first part is the input list and the second part is the graph structure:

Line 1 tells us 1_construct_wrapper.21, the name of the top MindSpore graph about the network, which is the entry graph.
Line 3 tells us how many inputs are in the network.
Line 5 to 6 are the input list, which is in the format of %para[No.]_[name] : <[data_type]x[shape]>.
Line 8 tells us the number of subgraph parsed by the network. There are 3 graphs in this IR. Line 42 is the entry graph 1_construct_wrapper.21. Line 32 is graph 3_func.23, parsed from the func(x, y) defined in the network. Line 12 is graph 2_construct.22, parsed from the function construct.

Taking graph 2_construct.22 as an example:

Line 10 to 28 indicate the graph structure, which contains several nodes, namely, CNode. In this example, there are Sub, Add, Mul defined in the function __init__.
Line 19 shows that figure 3_func.23 is called in the form of call @3_func.23, corresponding to the execution of the two-digit division of the function func in the script.

The CNode (check the design of ANF-IR) information format is as follows: from left to right, the ordinal number, node name - debug_name, operator name - op_name, input node - arg, attributes of the node - primitive_attrs, input and output specifications, source code parsing call stack and other information. Because the ANF graph is a unidirectional acyclic graph, the connection between nodes is displayed only based on the input relationship. The corresponding source code reflects the relationship between the CNode and the script source code. For example, line 15 is parsed from a = self.sub(x, 1).

  %[No.]([debug_name]) = [op_name]([arg], ...) primitive_attrs: {[key]: [value], ...}
      : (<[input data_type]x[input shape]>, ...) -> (<[output data_type]x[output shape]>, ...)
      # Corresponding source code

About the corresponding source code:

There are two mode for the corresponding source code displaying. The first mode is to display the complete call stack, such as 15_execute_0141.ir on the frontend and graph_build_0_136.ir on the backend. The second mode only displays one code line for reducing the size of the IR file, which eliminates the call stack, such as 04_abstract_specialize_0012.ir.
If the operator is a back propagation operator, the associated code line will not only display its own code, but also the corresponding forward code, identified by “Corresponding forward node candidate:”.
If the operator is a fusion operator, the associated code line will display the fusion related code, identified by “Corresponding code candidate:”, where the separator “-” is used to distinguish different codes.

After several optimizations by the compiler, the node may undergo several changes (such as operator splitting and operator merging). The source code parsing call stack information of the node may not be in a one-to-one correspondence with the script. This is only an auxiliary method.

After the kernel select phase at the backend, two lines of input and output specification information (that is, the content after :) will appear. The first line represents the specifications on the HOST side, and the second line represents the specifications on the DEVICE side.

dat Introduction

Use a text editing software (for example, vi) to open the 04_abstract_specialize_0013.dat file. The file contents are as follows (Here is MindSpore 1.6, and the content may have some imperceptible changes with the version upgrade):

# [No.1] 1_construct_wrapper.21
# In file train.py(33)/    def construct(self, x, y):/
funcgraph fg_21(
       %para1 : Tensor(F32)[]    # x
       , %para2 : Tensor(F32)[]    # y
   ) {
   %1 : Tensor(F32)[] = FuncGraph::fg_22(%para1, %para2)    #(Tensor(F32)[], Tensor(F32)[])    # fg_22=2_construct.22 #scope: Default
     # In file train.py(37)/        return c/#[CNode]2
   Primitive::Return{prim_type=1}(%1)    #(Tensor(F32)[]) #scope: Default
     # In file train.py(37)/        return c/#[CNode]1
}
# order:
#   1: 1_construct_wrapper.21:[CNode]2{[0]: ValueNode<FuncGraph> 2_construct.22, [1]: x, [2]: y}
#   2: 1_construct_wrapper.21:[CNode]1{[0]: ValueNode<Primitive> Return, [1]: [CNode]2}
 15
 16
# [No.2] 2_construct.22
# In file train.py(33)/    def construct(self, x, y):/
funcgraph fg_22(
       %para3 : Tensor(F32)[]    # x
       , %para4 : Tensor(F32)[]    # y
   ) {
   %1 : Tensor(F32)[] = PrimitivePy::Sub{prim_type=2}[input_names=["x", "y"], output_names=["output"]](%para3, Tensor(43)[])    #(Tensor(F32)[], Tenso    r(F32)[]) #scope: Default
     # In file train.py(34)/        a = self.sub(x, 1)/#a
   %2 : Tensor(F32)[] = PrimitivePy::Add{prim_type=2}[input_names=["x", "y"], output_names=["output"]](%1, %para4)    #(Tensor(F32)[], Tensor(F32)[])     #scope: Default
     # In file train.py(35)/        b = self.add(a, y)/#b
   %3 : Tensor(F32)[] = FuncGraph::fg_23(%1, %2)    #(Tensor(F32)[], Tensor(F32)[])    # fg_23=3_func.23 #scope: Default
     # In file train.py(36)/        c = self.mul(b, self.func(a, b))/#[CNode]5
   %4 : Tensor(F32)[] = PrimitivePy::Mul{prim_type=2}[input_names=["x", "y"], output_names=["output"]](%2, %3)    #(Tensor(F32)[], Tensor(F32)[]) #sco    pe: Default
     # In file train.py(36)/        c = self.mul(b, self.func(a, b))/#c
   Primitive::Return{prim_type=1}(%4)    #(Tensor(F32)[]) #scope: Default
     # In file train.py(37)/        return c/#[CNode]4
}
# order:
#   1: 2_construct.22:a{[0]: ValueNode<PrimitivePy> Sub, [1]: x, [2]: ValueNode<Tensor> Tensor(shape=[], dtype=Float32, value= 1)}
#   2: 2_construct.22:b{[0]: ValueNode<PrimitivePy> Add, [1]: a, [2]: y}
#   3: 2_construct.22:[CNode]5{[0]: ValueNode<FuncGraph> 3_func.23, [1]: a, [2]: b}
#   4: 2_construct.22:c{[0]: ValueNode<PrimitivePy> Mul, [1]: b, [2]: [CNode]5}
#   5: 2_construct.22:[CNode]4{[0]: ValueNode<Primitive> Return, [1]: c}
 40
 41
# [No.3] 3_func.23
# In file train.py(30)/    def func(x, y):/
funcgraph fg_23(
       %para5 : Tensor(F32)[]    # x
       , %para6 : Tensor(F32)[]    # y
   ) {
   %1 : Tensor(F32)[] = PrimitivePy::Div{prim_type=2}[input_names=["x", "y"], output_names=["output"]](%para5, %para6)    #(Tensor(F32)[], Tensor(F32)    []) #scope: Default
     # In file train.py(31)/        return self.div(x, y)/#[CNode]20
   Primitive::Return{prim_type=1}(%1)    #(Tensor(F32)[]) #scope: Default
     # In file train.py(31)/        return self.div(x, y)/#[CNode]19
}
# order:
#   1: 3_func.23:[CNode]20{[0]: ValueNode<PrimitivePy> Div, [1]: x, [2]: y}
#   2: 3_func.23:[CNode]19{[0]: ValueNode<Primitive> Return, [1]: [CNode]20}
 56
 57
# num of total function graphs: 3

Above, it lists all the graphs beginning with the entry graph. Line 1 indicates graph 1_construct_wrapper.21 whose id is No.1. And line 7 calls graph 2_construct.22. Line 17 to 39 show the information of graph 2_construct.22.

Taking graph 2_construct.22 whose information is located at Line 17 to 39 as an example:

Line 18 tells us which function this graph is parsed from.
Line 20 to 21 indicates the input information which is in the format of %para[No.] : [data_type][shape] # [name].
Line 23 to 32 indicates the graph structure, which contains several nodes, namely, CNode. In this example, there are Sub, Add, Mul. They are defined in the function __init__.
Line 34 to 39 shows the execution order of the compute nodes in the graph, corresponding to the order of code execution. The information format is: No.: belonging graph:node name{[0]: the first input, [1]: the second input, ...}. For CNode, the first input indicates how to compute for this CNode.
Line 58 indicates the number of graphs. Here is 3.

The CNode (check the design of ANF-IR) information format is as follows: including the node name, attribute, input node, output information, format and the corresponding source code.

%[No,] : [outputs' Spec] = [op_name]{[prim_type]}[attr0, attr1, ...](arg0, arg1, ...)    #(inputs' Spec)#[scope]
  # Corresponding source code/#debug_name

dot Introduction

We can use this file by graphviz as the input to generate images for users to view the model structure. For example, under the Linux operating system, we can convert a PNG image by the following command.

dot -Tpng -o 04_abstract_specialize_0014.png 04_abstract_specialize_0014.dot

The transformed image is shown below, and we can visually see the model structure. The different black boxes distinguish different subgraphs, and the blue arrows between graphs represent calling another graph. The blue area represents the parameter, the rectangle represents the parameter list of the graph, the hexagon and the black arrow represent the parameter as the input of the CNode to participate in the calculation process. The yellow rectangle represents the CNode. As can be seen from the picture, the CNode input starts from index 0, and the 0th input (that is, the purple or green area) represents what calculation the operator will perform, which is connected by a dotted arrow. The type is usually an operator primitive, or it can also be another graph. The rest inputs are the parameters required for the calculation.

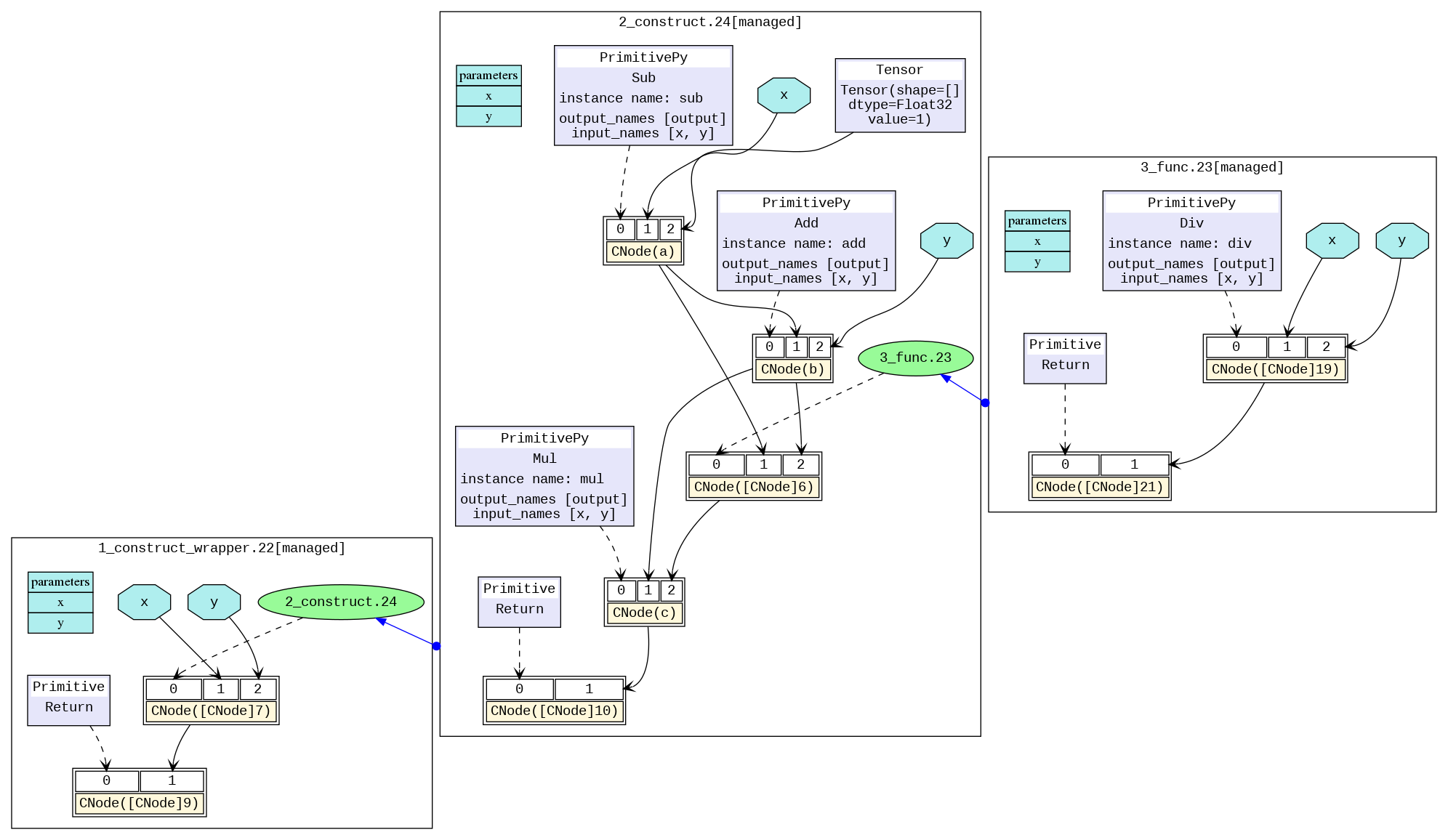
For models with multiple operators, the picture will be very large. It is recommended by using the visualization component MindInsight to visualize compute graphs.

How to derive the cause of the failure based on the analyze_fail.dat file analysis graph

In the process of MindSpore compiling a graph, the exceptions about graph evaluating fail usually happen. But we can find the reason by analyzing the exception information and analyze_fail.dat.

Example 1: parameters number mismatch

import mindspore as ms
import mindspore.nn as nn
from mindspore.nn import Cell
from mindspore import ops
  5
ms.set_context(mode=ms.GRAPH_MODE)
ms.set_context(save_graphs=True)
  8
class Net(nn.Cell):
  def __init__(self):
      super().__init__()
      self.add = ops.Add()
      self.sub = ops.Sub()
      self.mul = ops.Mul()
      self.div = ops.Div()
 16
  def func(x, y):
      return self.div(x, y)
 19
  def construct(self, x, y):
      a = self.sub(x, 1)
      b = self.add(a, y)
      c = self.mul(b, self.func(a, a, b))
      return c
 25
input1 = ms.Tensor(3, ms.float32)
input2 = ms.Tensor(2, ms.float32)
net = Net()
out = net(input1, input2)
print(out)

An error happens.

[EXCEPTION] ANALYZER(31946,7f6f03941740,python):2021-09-18-15:10:49.094.863 [mindspore/ccsrc/pipeline/jit/static_analysis/stack_frame.cc:85] DoJump] The parameters number of the function is 2, but the number of provided arguments is 3.
FunctionGraph ID : func.18
NodeInfo: In file test.py(17)
   def func(x, y):
  5
Traceback (most recent call last):
 File "test.py", line 29, in <module>
   out = net(input1, input2)
 File "/home/workspace/mindspore/mindspore/nn/cell.py", line 404, in __call__
   out = self.compile_and_run(*inputs)
 File "/home/workspace/mindspore/mindspore/nn/cell.py", line 682, in compile_and_run
   self.compile(*inputs)
 File "/home/workspace/mindspore/mindspore/nn/cell.py", line 669, in compile
   _cell_graph_executor.compile(self, *inputs, phase=self.phase, auto_parallel_mode=self._auto_parallel_mode)
 File "/home/workspace/mindspore/mindspore/common/api.py", line 542, in compile
   result = self._graph_executor.compile(obj, args_list, phase, use_vm, self.queue_name)
TypeError: mindspore/ccsrc/pipeline/jit/static_analysis/stack_frame.cc:85 DoJump] The parameters number of the function is 2, but the number of provided arguments is 3.
FunctionGraph ID : func.18
NodeInfo: In file test.py(17)
   def func(x, y):
 21
The function call stack (See file '/home/workspace/mindspore/rank_0/om/analyze_fail.dat' for more details):
# 0 In file test.py(24)
       return c
       ^
# 1 In file test.py(23)
       c = self.mul(b, self.func(a, a, b))
                       ^

Above exception is “TypeError: mindspore/ccsrc/pipeline/jit/static_analysis/stack_frame.cc:85 DoJump] The parameters number of the function is 2, but the number of provided arguments is 3…”. And it tells us FunctionGraph ID : func.18 only needs two parameters, but actually gives 3. We can find the related code is self.func(a, a, b) from ‘The function call stack … In file test.py(23)’. Easily, by checking the code, we know that we gave too much parameter to the calling function.

Sometimes when the exception information is not enough easy to understand, or we want to see the part of graph information that have evaluated, we use text editing software (e.g., vi) to open the file (in parentheses on line 20) that prompts in the error message: /home/workspace/mindspore/rank_0/om/analyze_fail.dat with the following content (Here is MindSpore 1.6, and the content may have some imperceptible changes with the version upgrade):

# [No.1] construct_wrapper.0
# In file test.py(22)/    def construct(self, x, y):/
funcgraph fg_0(
       %para1 : Tensor(F32)[]    # x
       , %para2 : Tensor(F32)[]    # y
   ) {
  7
#------------------------> 0
   %1 = FuncGraph::fg_3(%para1, %para2)    #(Tensor(F32)[], Tensor(F32)[])    # fg_3=construct.3 #scope: Default
     # In file test.py(26)/        return c/#[CNode]2
   Primitive::Return{prim_type=1}(%1)    #(Undefined) #scope: Default
     # In file test.py(26)/        return c/#[CNode]1
}
# order:
#   1: construct_wrapper.0:[CNode]2{[0]: ValueNode<FuncGraph> construct.3, [1]: x, [2]: y}
#   2: construct_wrapper.0:[CNode]1{[0]: ValueNode<Primitive> Return, [1]: [CNode]2}
 17
 18
# [No.2] construct.3
# In file test.py(22)/    def construct(self, x, y):/
funcgraph fg_3(
       %para3 : Tensor(F32)[]    # x
       , %para4 : Tensor(F32)[]    # y
   ) {
   %1 : Tensor(F32)[] = DoSignaturePrimitive::S-Prim-Sub{prim_type=1}[input_names=["x", "y"], output_names=["output"]](%para3, I64(1))    #(Tensor(F32)[], I64) #scope: Default
     # In file test.py(23)/        a = self.sub(x, 1)/#a
   %2 : Tensor(F32)[] = DoSignaturePrimitive::S-Prim-Add{prim_type=1}[input_names=["x", "y"], output_names=["output"]](%1, %para4)    #(Tensor(F32)[], Tensor(F32)[]) #scope: Default
     # In file test.py(24)/        b = self.add(a, y)/#b
 29
#------------------------> 1
   %3 = FuncGraph::fg_18(%1, %1, %2)    #(Tensor(F32)[], Tensor(F32)[], Tensor(F32)[])    # fg_18=func.18 #scope: Default
     # In file test.py(25)/        c = self.mul(b, self.func(a, a, b))/#[CNode]5
   %4 = DoSignaturePrimitive::S-Prim-Mul{prim_type=1}[input_names=["x", "y"], output_names=["output"]](%2, %3)    #(Tensor(F32)[], Undefined) #scope: Default
     # In file test.py(25)/        c = self.mul(b, self.func(a, a, b))/#c
   Primitive::Return{prim_type=1}(%4)    #(Undefined) #scope: Default
     # In file test.py(26)/        return c/#[CNode]4
}
# order:
#   1: construct.3:a{[0]: a, [1]: ValueNode<Int64Imm> 1, [2]: ValueNode<Float> Float32}
#   2: construct.3:a{[0]: ValueNode<DoSignaturePrimitive> S-Prim-Sub, [1]: x, [2]: ValueNode<Int64Imm> 1}
#   3: construct.3:b{[0]: ValueNode<DoSignaturePrimitive> S-Prim-Add, [1]: a, [2]: y}
#   4: construct.3:[CNode]5{[0]: ValueNode<FuncGraph> func.18, [1]: a, [2]: a, [3]: b}
#   5: construct.3:c{[0]: ValueNode<DoSignaturePrimitive> S-Prim-Mul, [1]: b, [2]: [CNode]5}
#   6: construct.3:[CNode]4{[0]: ValueNode<Primitive> Return, [1]: c}
 45
 46
#===============================================================================
# num of function graphs in stack: 2

The file analyze_fail.dat has the same information format with the file .dat. The only difference is analyze_fail.dat will locate the node which inferring failed. Searching the point by the text of ------------------------>, we reach the last position of the ------------------------> 1 at line 30. This last arrow points to the node that derives the error, which is %3 = FuncGraph::fg_18(%1, %1, %2)..., which expresses the information of the node in IR. How to view the dat file has been described in the Dat File Introduction section earlier, and will not be repeated here. The node at line 31 to 32 have an error. Its IR expression is %3 = FuncGraph::fg_18(%1, %1, %2) .... We can know the node have 3 parameters from (%1, %1, %2). From the source parsing call stack, it can be known that the function is actually self.func, which is defined in the script as def dunc(x, y):.... In the function definition, only two parameters are needed, so there will be a deduction failure error, and we need to modify the number of parameters passed in the script to solve the problem.

Example 2: BiasAdd inputs shape mismatch

import numpy as np
import mindspore
from mindspore import nn, ops, context, Tensor, Parameter
from mindspore.common.initializer import initializer
  5
class Net(nn.Cell):
 def __init__(self):
   super(Net, self).__init__()
   self.weight = Parameter(initializer('normal', [32, 8]), name="weight")
   self.bias = Parameter(initializer('zeros', [4]), name="bias")
 11
   self.matmul = ops.MatMul()
   self.bias_add = ops.BiasAdd()
 14
 def construct(self, x1):
   x = self.matmul(x1, self.weight)
   x = self.bias_add(x, self.bias)
   return x
 19
net = Net()
x = Tensor(np.arange(3*32).reshape(3, 32), mindspore.float32)
out = net(x)
print('out', out.shape)

An error happens.

 Traceback (most recent call last):
  File "test.py", line 22, in <module>
    out = net(x)
  File "/home/workspace/mindspore/build/package/mindspore/nn/cell.py", line 573, in __call__
    out = self.compile_and_run(*args)
  File "/home/workspace/mindspore/build/package/mindspore/nn/cell.py", line 956, in compile_and_run
    self.compile(*inputs)
  File "/home/workspace/mindspore/build/package/mindspore/nn/cell.py", line 929, in compile
    _cell_graph_executor.compile(self, *inputs, phase=self.phase, auto_parallel_mode=self._auto_parallel_mode)
  File "/home/workspace/mindspore/build/package/mindspore/common/api.py", line 1076, in compile
    result = self._graph_executor.compile(obj, args_list, phase, self._use_vm_mode())
ValueError: For 'BiasAdd', bias[0] shape must be equal to input_x[1] shape when data_format is NHWC or input_x[1] shape, but got bias[0] shape: 4, input_x[1] or input_x[1] shape: 8.

----------------------------------------------------
- The Traceback of Net Construct Code:
----------------------------------------------------
The function call stack (See file '/home/workspace/mindspore/rank_0/om/analyze_fail.dat' for more details. Get instructions about `analyze_fail.dat` at https://www.mindspore.cn/search?inputValue=analyze_fail.dat):
# 0 In file test.py(17)
    x = self.bias_add(x, self.bias)
        ^

----------------------------------------------------
- C++ Call Stack: (For framework developers)
----------------------------------------------------
mindspore/core/ops/bias_add.cc:71 BiasAddInferShape

The above reports that the errors is caused by the mismatching of the shape of the first input and the second input of the operator BiasAdd. To further understand what changes have taken place in the shape of the operator, we use text editing software (e.g., vi) to open the file that prompts in the error message: /home/workspace/mindspore/rank_0/om/analyze_fail.dat with the following content (Here is MindSpore 1.8, and the content may have some imperceptible changes with the version upgrade):

# 1.This file shows the parsed IR info when graph evaluating failed to help find the problem.
# 2.You can search the last `------------------------>` to the node which is inferred failed.
# 3.Refer to https://www.mindspore.cn/search?inputValue=analyze_fail.dat to get more instructions.
# ===============================================================================
  5
# [No.1] construct_wrapper.1
# In file test.py(15)/  def construct(self, x1):/
funcgraph fg_1(
       %para1 : Tensor(F32)[3, 32]    # x1
       , %para2 : Ref[Tensor(F32)][4]    # bias
       , %para3 : Ref[Tensor(F32)][32, 8]    # weight
   ) {
 13
#------------------------> 0
   %1 = FuncGraph::fg_2(%para1)    #(Tensor(F32)[3, 32])    # fg_2=construct.2 #scope: Default
#[CNode]3
   Primitive::Return{prim_type=1}(%1)    #(Undefined) #scope: Default
     # In file test.py(18)/    return x/#[CNode]4
}
# order:
#   1: construct_wrapper.1:[CNode]3{[0]: ValueNode<FuncGraph> construct.2, [1]: x1}
#   2: construct_wrapper.1:[CNode]4{[0]: ValueNode<Primitive> Return, [1]: [CNode]3}
 23
 24
# [No.2] construct.2
# In file test.py(15)/  def construct(self, x1):/
funcgraph fg_2[fg_1](
       %para4 : Tensor(F32)[3, 32]    # x1
   ) {
   %1 : Tensor(F32)[3, 8] = DoSignaturePrimitive::S-Prim-MatMul{prim_type=1}[output_names=["output"], transpose_a=Bool(0), input_names=["x1", "x2"], transpose_x2=Bool(0), transpose_x1    =Bool(0), transpose_b=Bool(0)](%para4, %para3)    #(Tensor(F32)[3, 32], Ref[Tensor(F32)][32, 8]) #scope: Default
     # In file test.py(16)/    x = self.matmul(x1, self.weight)/#x
 32
#------------------------> 1
   %2 = DoSignaturePrimitive::S-Prim-BiasAdd{prim_type=1}[output_names=["output"], format="NCHW", input_names=["x", "b"]](%1, %para2)    #(Tensor(F32)[3, 8], Ref[Tensor(F32)][4]) #sco    pe: Default
     # In file test.py(17)/    x = self.bias_add(x, self.bias)/#x
   Primitive::Return{prim_type=1}(%2)    #(Undefined) #scope: Default
     # In file test.py(18)/    return x/#[CNode]5
}
# order:
#   1: construct.2:x{[0]: ValueNode<DoSignaturePrimitive> S-Prim-MatMul, [1]: x1, [2]: weight}
#   2: construct.2:x{[0]: ValueNode<DoSignaturePrimitive> S-Prim-BiasAdd, [1]: x, [2]: bias}
#   3: construct.2:[CNode]5{[0]: ValueNode<Primitive> Return, [1]: x}
 43
 44
#===============================================================================
# num of function graphs in stack: 2/3 (Ignored 1 internal frames).

Search ------------------------> to the position where inferring failed at line 33. According to ...(%1, %para2) #(Tensor(F32)[3, 8], Ref[Tensor(F32)][4]), BiasAdd’s inputs are %1 and %para2. That %1’ with shape [3, 8] and %para2 with shape [4] doesn’t meet the requirement about bias (Tensor) - The bias tensor, with shape (C). C must be the same as channel dimension C of input_x... for BiasAdd API. Thus, an error happens.

To solve this problem, we need modify the shape of %1 or %para2 (namely self.bias).

For %para2 (namely self.bias), we modify the shape of self.bias by self.bias = Parameter(initializer('zeros', [8]), name="bias").
For %1, we need know what %1 is. According to line 30, %1 is a MatMul with output shape [3, 8]. Its inputs are (%para4, %para3). The first input (namely given arg x) shape is [3, 32] and the second input (namely self.weight) shape is [32, 8]. To meet the requirement of BiasAdd with the data shape [4], the shape of %1 output needs to be [3, 4]. Therefore, we modify self.weight by self.weight = Parameter(initializer('normal', [32, 4]), name="weight").