量子相位估计算法

概述

量子相位估计算法(Quantum Phase Estimation Algorithm，简称QPE)，是很多量子算法的关键。假设一个幺正算符 \(U\)，这个幺正算符作用在其本征态 \(|u\rangle\) 上会出现一个相位 \(e^{2\pi i \varphi}\)，现在我们假设 \(U\) 算符的本征值未知，也就是 \(\varphi\) 未知，但是 \(U\) 算符和本征态 \(|u\rangle\) 已知，相位估计算法的作用就是对这个相位 \(\varphi\) 进行估计。

算法解析

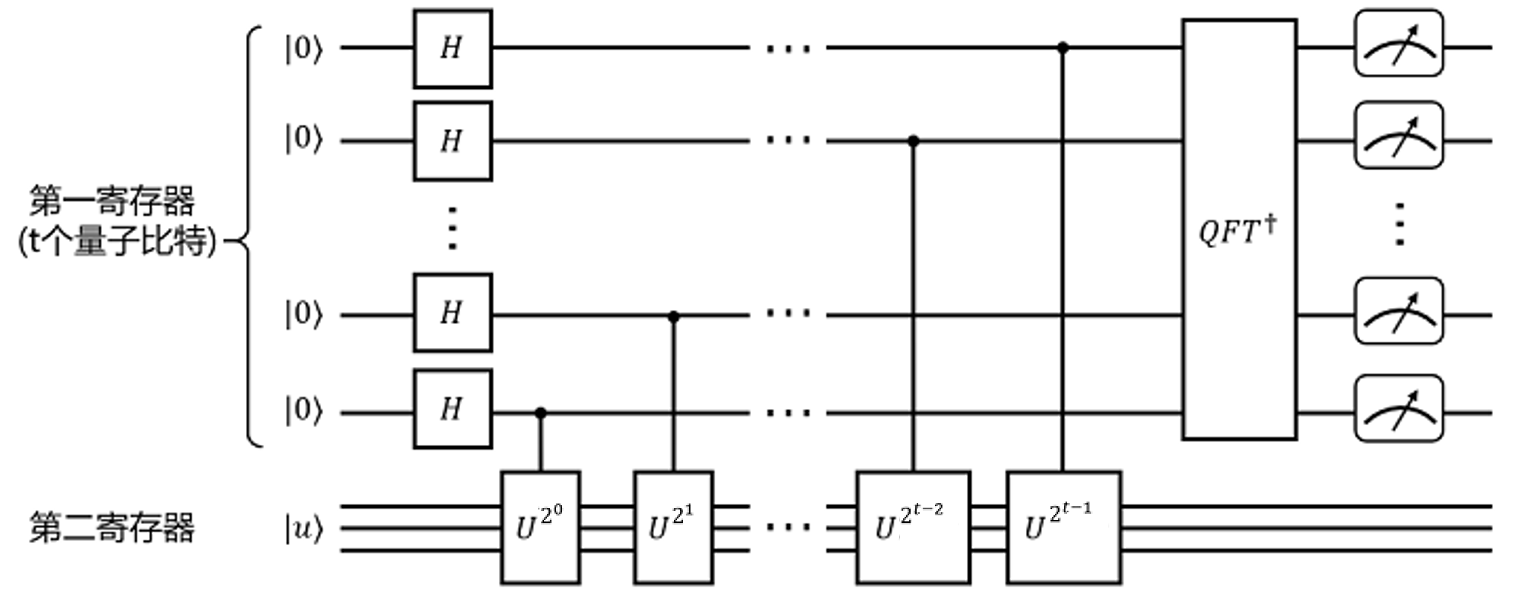
量子相位估计算法的实现需要两个寄存器(register)，第一寄存器包含\(t\)个初始在 \(|0\rangle\) 的量子比特，比特数和最后相位估计的结果的精度和算法的成功概率相关；第二个寄存器初始化在幺正算符 \(U\) 的本征态 \(|u\rangle\) 上。相位估计算法主要分为三步：

1. 对第一寄存器的所有量子比特进行 Hadamard 门操作，对第二寄存器连续进行 控制U 门操作，其中 \(U\) 门的幂次依次为 \(2^0, 2^1,...,2^{t-1}\)，控制比特依次为 \(q_{t-1}, q_{t-2},..., q_{1}, q_{0}\)。这时第一寄存器中的态就会变为

\[|\psi_1\rangle=\frac{1}{2^{t/2}}\left(|0\rangle+e^{i2\pi 2^{t-1}\varphi}|1\rangle\right)\left(|0\rangle+e^{i2\pi2^{t-2}\varphi}|1\rangle\right)...\left(|0\rangle+e^{i2\pi 2^{0}\varphi}|1\rangle\right) = \frac{1}{2^{t/2}}\sum_{k=0}^{2^t-1}e^{i2\pi\varphi k}|k\rangle\]

其中\(k\)为直积态的十进制表示，比如 \(k=0\) 表示第一寄存器中t个比特全部在基态 \(|00...00\rangle\), \(k=2\) 表示 \(|00...10\rangle\)，以此类推。

2. 对第一寄存器的进行量子傅里叶变换的逆变换(Inverse Quantum Fourier Transform)，在线路中表示成 \(QFT^\dagger\), 对 \(|\psi_1\rangle\) 进行逆量子傅里叶变换可得 \(|\psi_2\rangle\)

\[|\psi_2\rangle=QFT^\dagger|\psi_1\rangle =\frac{1}{2^t}\sum_{x=0}^{2^t-1}a_x|x\rangle\]

其中

\[a_x=\sum_{k=0}^{2^t-1}e^{2\pi i k(\varphi-x/2^t)}\]

为本征基矢 \(|x\rangle\) (\(x=0.1,...,2^t\)) 对应的概率幅 。由上式可得，当 \(2^t\varphi\) 为整数，且满足 \(x=2^t\varphi\) 时，概率幅取最大值1，此时第一寄存器的末态可以精确反映 \(\varphi\)；当 \(2^t\varphi\) 不是整数时，\(x\) 为 \(\varphi\) 的估计，且\(t\)越大，估计精度越高。

3. 对第一寄存器的量子比特进行测量，得到第一寄存器的末态 \(f=\sum_{x}^{2^t-1}a_x|x\rangle\), \(x=0,1,...,2^t\)，从中找到最大的振幅 \(a_{max}\)，其对应的本征基矢 \(|x\rangle\) 中的 \(x\) 再除以 \(2^t\) 即为相位的估计值。

QPE代码实现

下面用一个实例来演示如何在MindQuantum实现量子相位估计算法，选择 T 门作为进行估计的幺正算符，由定义

\[T|1\rangle=e^{i\pi/4}|1\rangle\]

可知需要估计的相位角为 \(\varphi=\frac{1}{8}\)。

现在假设我们不知道 T 门的相位信息，只知道幺正算符 \(U\) 是 T 门且本征态为 \(|1\rangle\) ，接下来我们需要用量子相位估计算法求出其对应的本征值，即需要估计本征值指数上的相位角。

首先导入相关依赖。

from mindquantum.core import Circuit, UN, T, H, X, Power, BARRIER
from mindquantum.simulator import Simulator
from mindquantum.algorithm import qft
import numpy as np

UN 可以指定量子门，目标比特和控制比特，从而在线路中搭建门操作； Power 可以得到指定量子门的指数形式。因为我们已知 T 门的本征态为 \(|1\rangle\)，所以第二寄存器只需1个比特，而在第一寄存器中的比特数越多，得到的结果就越准确，在这里我们使用4个比特。

因此我们需要搭建5比特线路， \(q_0, q_1, q_2, q_3\) 比特用于估计，属于第一寄存器， \(q_4\) 属于第二寄存器用于传入 \(T\) 算符的本征态。

利用 UN 对 \(q_0, q_1, q_2, q_3\) 进行 Hadamard 门操作， 用 X 门对 \(q_4\) 进行翻转，得到 T 门的本征态 \(|1\rangle\)。

# pylint: disable=W0104
n = 4
circ = Circuit()
circ += UN(H, n) # 对前4个比特作用力H门
circ += X.on(n)  # 对q4作用X门
circ

q0: ──H──

q1: ──H──

q2: ──H──

q3: ──H──

q4: ──X──

以 \(q_4\) 为目标比特，添加控制\(T^{2^i}\)门。

# pylint: disable=W0104
for i in range(n):
    circ += Power(T, 2**i).on(n, n - i - 1) # 添加T^2^i门，其中q4为目标比特，n-i-1为控制比特
circ

q0: ──H──────────────────────────●───
                                 │
q1: ──H───────────────────●──────┼───
                          │      │
q2: ──H────────────●──────┼──────┼───
                   │      │      │
q3: ──H─────●──────┼──────┼──────┼───
            │      │      │      │
q4: ──X────T^1────T^2────T^4────T^8──

对第一寄存器中的比特进行逆量子傅里叶变换。

# pylint: disable=W0104
circ += BARRIER
circ += qft(range(n)).hermitian() # 对前4个比特作用量子傅立叶变换的逆变换
circ

q0: ──H──────────────────────────●──────────@───────────────────────────────────────────────────────PS(-π/8)────PS(-π/4)────PS(-π/2)────H──
                                 │          │                                                          │           │           │
q1: ──H───────────────────●──────┼─────@────┼──────────────────────────PS(-π/4)────PS(-π/2)────H───────┼───────────┼───────────●───────────
                          │      │     │    │                             │           │                │           │
q2: ──H────────────●──────┼──────┼─────@────┼─────────PS(-π/2)────H───────┼───────────●────────────────┼───────────●───────────────────────
                   │      │      │          │            │                │                            │
q3: ──H─────●──────┼──────┼──────┼──────────@────H───────●────────────────●────────────────────────────●───────────────────────────────────
            │      │      │      │
q4: ──X────T^1────T^2────T^4────T^8────────────────────────────────────────────────────────────────────────────────────────────────────────

选择后端、传入总比特数创建模拟器，对量子线路进行演化，得到末态。

# pylint: disable=W0104
from mindquantum import Measure
sim = Simulator('projectq', circ.n_qubits)                      # 创建模拟器
sim.apply_circuit(circ)                                         # 用模拟器演化线路
qs = sim.get_qs()                                               # 获得演化得到的量子态
res = sim.sampling(UN(Measure(), circ.n_qubits - 1), shots=100) # 在寄存器1中加入测量门并对线路进行100次采样，获得统计结果
res

shots: 100
Keys: q3 q2 q1 q0│0.00     0.2         0.4         0.6         0.8         1.0
─────────────────┼───────────┴───────────┴───────────┴───────────┴───────────┴
             0100│▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
                 │
{'0100': 100}

需要注意的是，测量结果作为二进制串的读取顺序应为\(|q_0q_1q_2q_3\rangle\)，因此我们得到寄存器1的测量结果为0010，概率幅为1，该末态可以精准地反映相位\(\varphi\)。但0010是二进制结果，因此我们将它转回十进制后再除以\(2^n\)，就得到了我们最终的估计值：\(\varphi=\frac{2}{2^4}=\frac{1}{8}\)。

我们也可以通过线路演化得到的量子态 qs 找出第一寄存器中振幅最大值 \(a_{max}\) 的位置，进而得到其对应的本征基矢 \(|x\rangle\) ，其中的 \(x\) 再除以 \(2^t\) 即为相位的估计值。

index = np.argmax(np.abs(qs))
print(bin(index)[2:])

10100

需要注意的是，qs 对应的是整个量子线路的末态，因此得到的 index 也包含第二寄存器中的比特，不能直接得到第一寄存器末态中 \(a_{max}\) 对应的 \(|x\rangle\) ，需要将 index 转成二进制后将 \(q4\) 对应的比特位剔除，然后得到的才是第一寄存器的 \(|x\rangle\) 。

bit_string = bin(index)[2:].zfill(circ.n_qubits)[1:]        # 将index转换成01串并剔除q4
bit_string = bit_string[::-1]                               # 将比特串顺序调整为q0q1q2q3
print(bit_string)

0010

再将二进制转回十进制，得到我们最终的估计值。

# pylint: disable=W0104
theta_exp = int(bit_string, 2) / 2**n
theta_exp

0.125

可见得到的估计相位和 \(\varphi\) 近似相等。

参考文献

[1] Michael A. Nielsen and Isaac L. Chuang. Quantum computation and quantum information