文档反馈

问题文档片段

问题文档片段包含公式时，显示为空格。

提交类型

issue

有点复杂...

找人问问吧。

PR

小问题，全程线上修改...

一键搞定！

请选择提交类型

问题类型

规范和低错类

- 规范和低错类：

- 错别字或拼写错误，标点符号使用错误、公式错误或显示异常。

- 链接错误、空单元格、格式错误。

- 英文中包含中文字符。

- 界面和描述不一致，但不影响操作。

- 表述不通顺，但不影响理解。

- 版本号不匹配：如软件包名称、界面版本号。

易用性

- 易用性：

- 关键步骤错误或缺失，无法指导用户完成任务。

- 缺少主要功能描述、关键词解释、必要前提条件、注意事项等。

- 描述内容存在歧义指代不明、上下文矛盾。

- 逻辑不清晰，该分类、分项、分步骤的没有给出。

正确性

- 正确性：

- 技术原理、功能、支持平台、参数类型、异常报错等描述和软件实现不一致。

- 原理图、架构图等存在错误。

- 命令、命令参数等错误。

- 代码片段错误。

- 命令无法完成对应功能。

- 界面错误，无法指导操作。

- 代码样例运行报错、运行结果不符。

风险提示

- 风险提示：

- 对重要数据或系统存在风险的操作，缺少安全提示。

内容合规

- 内容合规：

- 违反法律法规，涉及政治、领土主权等敏感词。

- 内容侵权。

请选择问题类型

问题描述

点击输入详细问题描述，以帮助我们快速定位问题。

文档反馈

二维黎曼问题

本案例要求MindSpore版本 >= 2.0.0调用如下接口: mindspore.jit，mindspore.jit_class。

黎曼问题，以伯恩哈德·黎曼命名，是由守恒方程和分段常数初始条件组成的特定初值问题，在研究区域内具有单个间断面。黎曼问题在理解欧拉方程等方程具有重要作用，因为该方程所有的性质，如冲击和稀疏波，都出现在黎曼问题的解中。此外，黎曼问题还给出了包括欧拉方程在内的一些复杂非线性方程的精确解。

在数值分析中，由于网格的离散性，很自然地，黎曼问题出现在守恒方程的有限体积求解中，因此，它被广泛应用在计算流体力学和计算磁流体力学的模拟中。

问题描述

二维黎曼问题的定义为：

\begin{array}{r} \frac{\partial}{\partial t} (\begin{array}{c} ρ \\ ρ u \\ ρ v \\ E \end{array}) + \frac{\partial}{\partial x} (\begin{array}{c} ρ u \\ ρ u^{2} + p \\ ρ u v \\ u (E + p) \end{array}) + \frac{\partial}{\partial y} (\begin{array}{c} ρ v \\ ρ u v \\ ρ v^{2} + p \\ v (E + p) \end{array}) = 0 \end{array}

E = \frac{ρ}{γ - 1} + \frac{1}{2} ρ u^{2}

其中，对理想气体， $γ = 1.4$ ，初始条件为：

\begin{array}{r} {(\begin{array}{c} ρ \\ u \\ v \\ p \end{array})}_{x < 0.5, y > 0.5} = (\begin{array}{c} 0.5323 \\ 1.206 \\ 0.0 \\ 0.3 \end{array}), {(\begin{array}{c} ρ \\ u \\ v \\ p \end{array})}_{x > 0.5, y > 0.5} = (\begin{array}{c} 1.5 \\ 0.0 \\ 0.0 \\ 1.5 \end{array}) \end{array}

\begin{array}{r} {(\begin{array}{c} ρ \\ u \\ v \\ p \end{array})}_{x < 0.5, y < 0.5} = (\begin{array}{c} 0.138 \\ 1.206 \\ 1.206 \\ 0.029 \end{array}), {(\begin{array}{c} ρ \\ u \\ v \\ p \end{array})}_{x > 0.5, y < 0.5} = (\begin{array}{c} 0.5323 \\ 0.0 \\ 1.206 \\ 0.3 \end{array}) \end{array}

本案例中src包可以在src下载。

[1]:

import mindspore as ms
from mindflow import load_yaml_config, vis_2d
from mindflow import cfd
from mindflow.cfd.runtime import RunTime
from mindflow.cfd.simulator import Simulator

from src.ic import riemann2d_ic

ms.set_context(device_target="GPU", device_id=3)

定义Simulator和RunTime

网格、材料、仿真时间、边界条件和数值方法的设置在文件numeric.yaml中。

[2]:

config = load_yaml_config('numeric.yaml')
simulator = Simulator(config)
runtime = RunTime(config['runtime'], simulator.mesh_info, simulator.material)

初始条件

根据网格坐标确定初始条件。

[3]:

mesh_x, mesh_y, _ = simulator.mesh_info.mesh_xyz()
pri_var = riemann2d_ic(mesh_x, mesh_y)
con_var = cfd.cal_con_var(pri_var, simulator.material)

执行仿真

随时间推进执行仿真。

[4]:

while runtime.time_loop(pri_var):
    pri_var = cfd.cal_pri_var(con_var, simulator.material)
    runtime.compute_timestep(pri_var)
    con_var = simulator.integration_step(con_var, runtime.timestep)
    runtime.advance()

current time = 0.000000, time step = 0.001005
current time = 0.001005, time step = 0.001005
current time = 0.002010, time step = 0.001005
current time = 0.003016, time step = 0.001005
current time = 0.004021, time step = 0.001005
current time = 0.005026, time step = 0.001005
current time = 0.006031, time step = 0.001005
current time = 0.007036, time step = 0.001005
current time = 0.008041, time step = 0.001005
current time = 0.009046, time step = 0.001005
current time = 0.010051, time step = 0.001005
current time = 0.011057, time step = 0.001005
current time = 0.012062, time step = 0.001005
current time = 0.013067, time step = 0.001005
current time = 0.014072, time step = 0.001005
current time = 0.015076, time step = 0.001005
current time = 0.016081, time step = 0.001005
current time = 0.017086, time step = 0.001005
current time = 0.018091, time step = 0.001005
current time = 0.019097, time step = 0.001005
current time = 0.020102, time step = 0.001005
current time = 0.021107, time step = 0.001005
current time = 0.022112, time step = 0.001005
current time = 0.023117, time step = 0.001005
current time = 0.024121, time step = 0.001005
current time = 0.025126, time step = 0.001005
current time = 0.026131, time step = 0.001005
current time = 0.027137, time step = 0.001005
current time = 0.028142, time step = 0.001005
...
current time = 0.297090, time step = 0.000760
current time = 0.297849, time step = 0.000759
current time = 0.298609, time step = 0.000759
current time = 0.299368, time step = 0.000759

仿真结果后处理

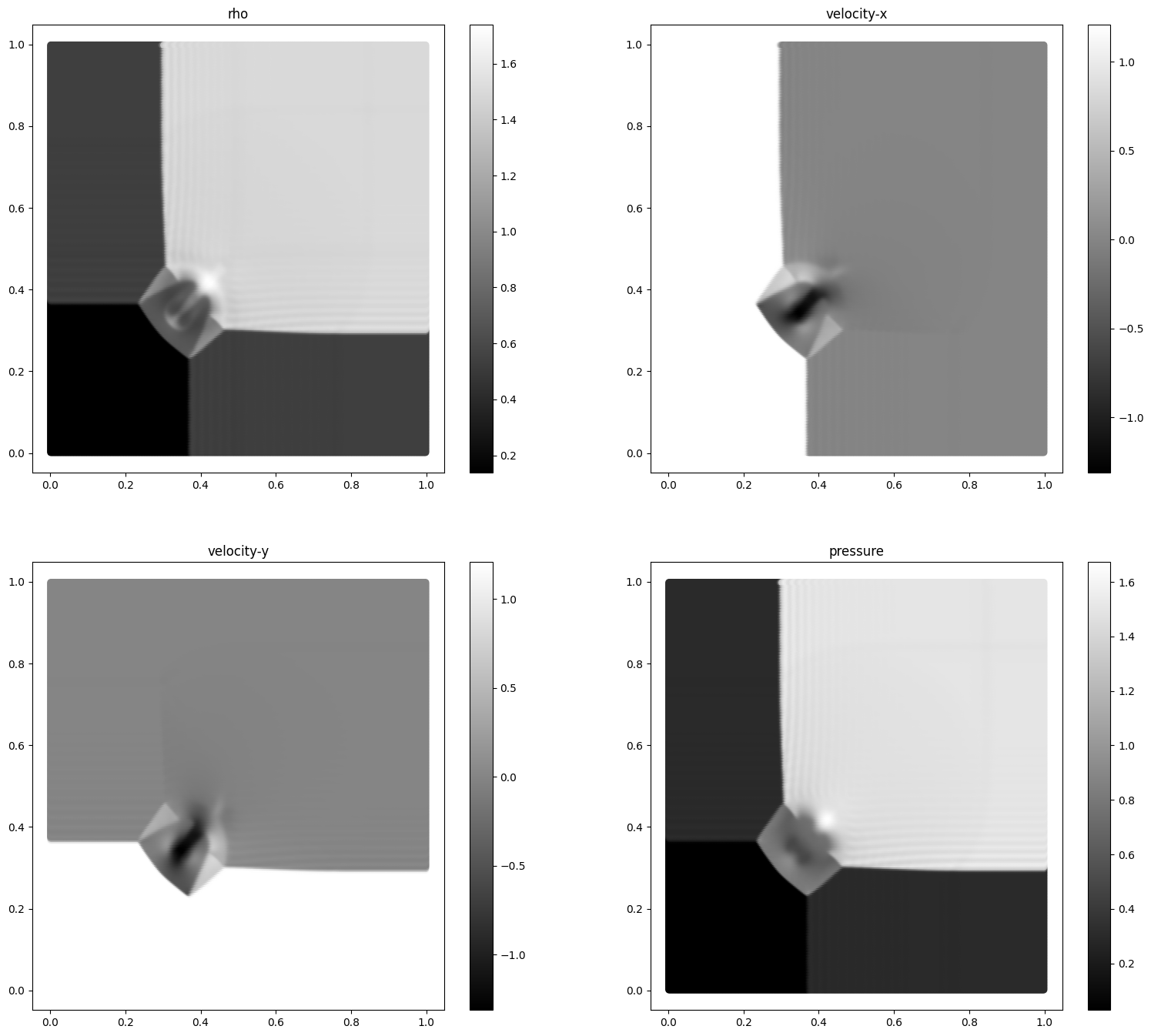
您可以对密度、压力、速度进行可视化。

[5]:

pri_var = cfd.cal_pri_var(con_var, simulator.material)
vis_2d(pri_var, 'riemann2d.jpg')

../_images/cfd_solver_riemann2d_10_0.png