感知量化训练
Ascend GPU 扩展功能
背景
随着深度学习的发展,神经网络被广泛应用于各种领域,模型性能提高的同时也引入了巨大的参数量和计算量。越来越多的应用选择在移动设备或者边缘设备上使用深度学习技术。
以手机为例,为了提供人性化和智能化的服务,操作系统和APP应用都开始集成AI功能。而使用该功能,涉及训练或者推理,自然包含大量的网络模型及权重文件。以经典的AlexNet为例,原始权重文件已经超过了200MB,而最近出现的新模型正往结构更复杂、参数更多的方向发展。
概述
由于移动设备、边缘设备的硬件资源有限,需要对模型进行精简,而量化(Quantization)技术就是应对该类问题衍生出的技术之一。模型量化是一种将浮点计算转成低比特定点计算的技术,可以有效地降低模型计算强度、参数大小和内存消耗,但往往带来巨大的精度损失。
量化方法
模型量化即以较低的推理精度损失将连续取值(或者大量可能的离散取值)的浮点型模型权重或流经模型的张量数据定点近似为(通常为int8)有限多个(或较少的)离散值的过程,它是以更少位数的数据类型用于近似表示32位有限范围浮点型数据的过程,而模型的输入输出依然是浮点型,从而达到减少模型尺寸大小、减少模型内存消耗及加快模型推理速度等目标。
首先量化会损失精度,这相当于给网络引入了噪声,但是神经网络一般对噪声是不太敏感的,只要控制好量化的程度,对高级任务精度影响可以做到很小。
其次,传统的卷积操作都是使用FP32浮点,浮点运算时需要很多时间周期来完成,但是如果我们将权重参数和激活在输入各个层之前量化到INT8,减少了位数和乘法操作,而且此时做的卷积操作都是整型的乘加运算,比浮点快很多。

如上图所示,与FP32类型相比,FP16、INT8等低精度数据表达类型所占用空间更小。使用低精度数据表达类型替换高精度数据表达类型,可以大幅降低存储空间和传输时间。而低比特的计算性能也更高,INT8相对比FP32的加速比可达到3倍甚至更高,对于相同的计算,功耗上也有明显优势。
当前业界量化方案主要分为两种:感知量化训练(Quantization Aware Training)和训练后量化(Post-training Quantization)。
1)感知量化训练需要训练数据,在模型准确率上通常表现更好,适用于对模型压缩率和模型准确率要求较高的场景。目的是减少精度损失,其参与模型训练的前向推理过程令模型获得量化损失的差值,但梯度更新需要在浮点下进行,因而其并不参与反向传播过程。
2)训练后量化简单易用,只需少量校准数据,适用于追求高易用性和缺乏训练资源的场景。
3)训练后校正量化同样是训练后静态量化,也称为校正量化或者数据集量化。其原理是在端侧低比特推理时,生成一个校准表来量化模型。
伪量化节点
伪量化节点,是指感知量化训练中插入的节点,用以寻找网络数据分布,并反馈损失精度,具体作用如下:
找到网络数据的分布,即找到待量化参数的最大值和最小值;
模拟量化为低比特时的精度损失,把该损失作用到网络模型中,传递给损失函数,让优化器在训练过程中对该损失值进行优化。
BatchNorm折叠
基本卷积Conv操作为:
大部分网络模型中为了对卷积后的数据进行规约,会使用BatchNorm层。因此Conv和BatchNorm两个算子在正向传播的时候,根据公式可以融合为一个算子,该操作称为BN折叠:
网络模型中经常使用BN层对数据进行规约,有效降低上下层之间的数据依赖性。然而大部分在推理框架当中都会对BN层和卷积操作进行融合,为了更好地模拟在推理时的算子融合操作,这里对BN层进行folding处理。MindSpore在进行感知量化训练的时候会默认进行BN折叠。
下面左边图是普通训练时模型,右边图是融合后推理时模型。
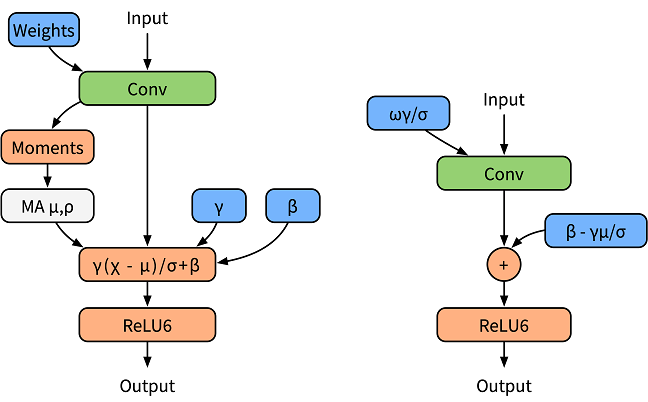
感知量化训练
MindSpore的感知量化训练是指在训练时使用伪量化节点来模拟量化操作,过程中仍然采用浮点数计算,并通过反向传播学习更新网络参数,使得网络参数更好地适应量化带来的损失。对于权值和数据的量化,MindSpore采用了参考文献[1]中的方案。
表1:感知量化训练规格
规格 |
规格说明 |
|---|---|
硬件支持 |
GPU、Ascend AI 910处理器的硬件平台 |
网络支持 |
已实现的网络包括LeNet、ResNet50等网络,具体请参见https://gitee.com/mindspore/models/tree/master。 |
算法支持 |
支持非对称和对称的量化算法;支持逐层和逐通道的量化算法。 |
方案支持 |
支持4、7和8比特的量化方案。 |
数据类型支持 |
Ascend平台支持精度为FP32和FP16的网络进行量化训练,GPU平台支持FP32。 |
运行模式支持 |
Graph模式 |
感知量化训练示例
感知量化训练与一般训练步骤一致,在定义量化网络和生成量化模型阶段需要进行额外的操作,完整流程如下:
加载数据集,处理数据。
定义量化网络。
定义优化器和损失函数。
训练网络,保存模型文件。
加载保存的模型,进行推理。
导出量化模型。
在上面流程中,步骤2和步骤6是感知量化训练区别普通训练需要额外进行的步骤。接下来,以LeNet网络为例,展开叙述量化相关步骤。
你可以在这里找到完整可运行的样例代码:https://gitee.com/mindspore/models/tree/r1.6/official/cv/lenet_quant 。
定义量化网络
量化网络是指在原网络定义的基础上修改需要量化的网络层后生成的带有伪量化节点的网络。根据构建量化网络的不同,定义量化网络可分为如下两种的方法:
自动构建量化网络:定义融合网络后,调用转换接口后会自动将融合网络转化为量化网络。用户无需感知插入伪量化节点的过程,更简单易用。
手动构建量化网络:手动将需要量化的网络层替换成对应的量化节点,或者直接在需要量化的网络层后插入伪量化节点,修改后的网络即量化网络。用户可以自定义需要量化的网络层,更加灵活易扩展。
自动构建量化网络方法支持量化的网络层包含
nn.Conv2dBnAct、nn.DenseBnAct、Add、Sub、Mul和RealDiv。如果只需量化这些网络层的部分层,或者要支持量化其他网络层,请使用手动构建量化网络方法。自动构建量化网络的转换接口是
QuantizationAwareTraining.quantize。
原网络模型LeNet5的定义如下所示:
class LeNet5(nn.Cell):
"""
Lenet network
Args:
num_class (int): Num classes. Default: 10.
num_channel (int): Num channel. Default: 1.
Returns:
Tensor, output tensor
Examples:
>>> LeNet(num_class=10, num_channel=1)
"""
def __init__(self, num_class=10, num_channel=1):
super(LeNet5, self).__init__()
self.conv1 = nn.Conv2d(num_channel, 6, 5, pad_mode='valid')
self.conv2 = nn.Conv2d(6, 16, 5, pad_mode='valid')
self.fc1 = nn.Dense(16 * 5 * 5, 120, weight_init=Normal(0.02))
self.fc2 = nn.Dense(120, 84, weight_init=Normal(0.02))
self.fc3 = nn.Dense(84, num_class, weight_init=Normal(0.02))
self.relu = nn.ReLU()
self.max_pool2d = nn.MaxPool2d(kernel_size=2, stride=2)
self.flatten = nn.Flatten()
def construct(self, x):
x = self.max_pool2d(self.relu(self.conv1(x)))
x = self.max_pool2d(self.relu(self.conv2(x)))
x = self.flatten(x)
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
return x
自动构建量化网络
首先定义融合网络:
使用
nn.Conv2dBnAct算子替换原网络模型中的2个算子nn.Conv2d和nn.ReLU。使用
nn.DenseBnAct算子替换原网络模型中的2个算子nn.Dense和nn.ReLU。
无论
nn.Dense和nn.Conv2d算子后面有没有nn.BatchNorm和nn.ReLU,都要按规定使用上述两个算子进行融合替换。
替换算子后的融合网络如下:
class LeNet5(nn.Cell):
def __init__(self, num_class=10):
super(LeNet5, self).__init__()
self.num_class = num_class
self.conv1 = nn.Conv2dBnAct(1, 6, kernel_size=5, pad_mode='valid', activation='relu')
self.conv2 = nn.Conv2dBnAct(6, 16, kernel_size=5, pad_mode='valid', activation='relu')
self.fc1 = nn.DenseBnAct(16 * 5 * 5, 120, activation='relu')
self.fc2 = nn.DenseBnAct(120, 84, activation='relu')
self.fc3 = nn.DenseBnAct(84, self.num_class)
self.max_pool2d = nn.MaxPool2d(kernel_size=2, stride=2)
self.flatten = nn.Flatten()
def construct(self, x):
x = self.max_pool2d(self.conv1(x))
x = self.max_pool2d(self.conv2(x))
x = self.flatten(x)
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
return x
使用感知量化训练进行微调时,需要加载预训练模型的参数。
from mindspore.compression.quant import load_nonquant_param_into_quant_net
...
# define fusion network
network = LeNet5(cfg.num_classes)
param_dict = load_checkpoint(args.ckpt_path)
load_nonquant_param_into_quant_net(network, param_dict)
然后使用QuantizationAwareTraining.quantize接口自动在融合网络中插入伪量化节点,将融合网络转化为量化网络。
from mindspore.compression.quant import QuantizationAwareTraining
quantizer = QuantizationAwareTraining(quant_delay=900,
bn_fold=False,
per_channel=[True, False],
symmetric=[True, False])
net = quantizer.quantize(network)
如果量化精度不满足要求,请先调整合适的量化策略参数。例如,一般量化bit数越大量化精度损失越小,权重采用逐通道量化会比逐层量化获取更好的精度。另外,还可以选择手动构建量化网络方法,通过手动选择量化部分网络层来平衡准确率和推理性能之间的关系。
手动构建量化网络
把原网络中需要量化的层替换成对应的量化算子:
使用
nn.Conv2dQuant替换原网络模型中的nn.Conv2d算子。使用
nn.DenseQuant替换原网络模型中nn.Dense算子。使用
nn.ActQuant替换原网络模型中的nn.ReLU算子。
class LeNet5(nn.Cell):
def __init__(self, num_class=10, channel=1):
super(LeNet5, self).__init__()
self.num_class = num_class
self.qconfig = create_quant_config(quant_dtype=(QuantDtype.INT8, QuantDtype.INT8), per_channel=(True, False), symmetric=[True, False])
self.conv1 = nn.Conv2dQuant(channel, 6, 5, pad_mode='valid', quant_config=self.qconfig, quant_dtype=QuantDtype.INT8)
self.conv2 = nn.Conv2dQuant(6, 16, 5, pad_mode='valid', quant_config=self.qconfig, quant_dtype=QuantDtype.INT8)
self.fc1 = nn.DenseQuant(16 * 5 * 5, 120, quant_config=self.qconfig, quant_dtype=QuantDtype.INT8)
self.fc2 = nn.DenseQuant(120, 84, quant_config=self.qconfig, quant_dtype=QuantDtype.INT8)
self.fc3 = nn.DenseQuant(84, self.num_class, quant_config=self.qconfig, quant_dtype=QuantDtype.INT8)
self.relu = nn.ActQuant(nn.ReLU(), quant_config=self.qconfig, quant_dtype=QuantDtype.INT8)
self.max_pool2d = nn.MaxPool2d(kernel_size=2, stride=2)
self.flatten = nn.Flatten()
def construct(self, x):
x = self.conv1(x)
x = self.relu(x)
x = self.max_pool2d(x)
x = self.conv2(x)
x = self.relu(x)
x = self.max_pool2d(x)
x = self.flatten(x)
x = self.fc1(x)
x = self.relu(x)
x = self.fc2(x)
x = self.relu(x)
x = self.fc3(x)
return x
量化算子:
nn.Conv2dQuant、nn.DenseQuant、nn.ActQuant等为含有伪量化节点的算子。更多的量化算子内容请见 quantized-functions。在需要量化的网络层后面插入伪量化节点
nn.FakeQuantWithMinMaxObserver可以实现更多网络层的量化。建议优先选择量化网络中靠后的层,因为量化前面的网络层可能会造成更多的精度损失。
使用感知量化训练进行微调时,需要加载预训练模型的参数。
from mindspore.compression.quant import load_nonquant_param_into_quant_net
...
# define quant network
network = LeNet5(cfg.num_classes)
param_dict = load_checkpoint(args.ckpt_path)
load_nonquant_param_into_quant_net(network, param_dict)
虽然面向用户API层的使用方式跟正常的使用方式相差不大,但是MindSpore引入了伪量化节点和BN折叠操作,下面左边为原始论文[1]中设计BN折叠训练图,右边是实际MindSpore执行经过优化融合的训练图。
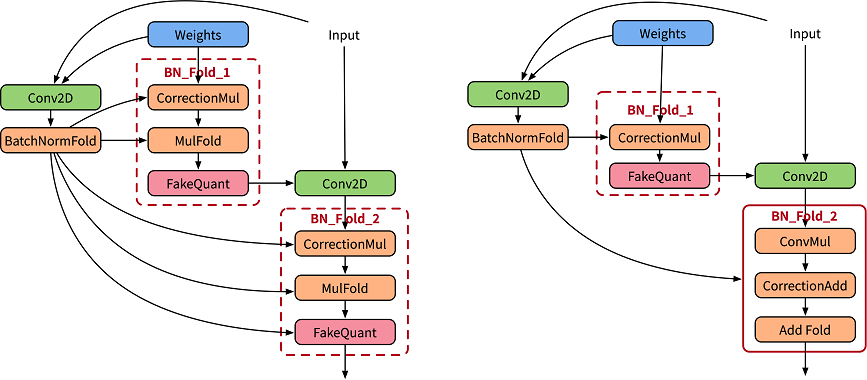
导出量化模型
在端侧硬件平台上部署的量化模型为通用模型格式(AIR、MindIR等),并且不包含伪量化节点。导出步骤为:
定义量化网络。该步骤的量化网络和感知量化训练时的量化网络相同。
加载感知量化训练时保存的CheckPoint格式文件。
导出量化模型。设置
export接口的quant_mode、mean和std_dev参数。
from mindspore import Tensor, context, load_checkpoint, load_param_into_net, export
if __name__ == "__main__":
...
# define fusion network
network = LeNet5(cfg.num_classes)
quantizer = QuantizationAwareTraining(bn_fold=False,
per_channel=[True, False],
symmetric=[True, False])
network = quantizer.quantize(network)
# load quantization aware network checkpoint
param_dict = load_checkpoint(args.ckpt_path)
load_param_into_net(network, param_dict)
# export network
inputs = Tensor(np.ones([1, 1, cfg.image_height, cfg.image_width]), mindspore.float32)
export(network, inputs, file_name="lenet_quant", file_format='MINDIR', quant_mode='QUANT', mean=127.5, std_dev=127.5)
导出量化模型后,请使用MindSpore进行推理。
导出的模型格式支持MindIR和AIR。
感知量化训练后导出的模型支持端侧推理和Ascend 310 AI处理器上推理。
参考文献
[1] Jacob B, Kligys S, Chen B, et al. Quantization and training of neural networks for efficient integer-arithmetic-only inference[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 2704-2713.

