MindSpore IR(MindIR)
Linux Windows Ascend GPU 框架开发 中级 模型开发 高级 贡献者
简介
中间表示(IR)是程序编译过程中介于源语言和目标语言之间的程序表示,以方便编译器进行程序分析和优化,因此IR的设计需要考虑从源语言到目标语言的转换难度,同时考虑程序分析和优化的易用性和性能。
MindIR是一种基于图表示的函数式IR,其最核心的目的是服务于自动微分变换。自动微分采用的是基于函数式编程框架的变换方法,因此IR采用了接近于ANF函数式的语义。此外,借鉴Sea of Nodes[1]和Thorin[2]的优秀设计,采用了一种基于显性依赖图的表示方式。关于ANF-IR的具体介绍,可以参考MindSpore IR文法定义。
在图模式context.set_context(mode=context.GRAPH_MODE)下运行用MindSpore编写的模型时,若配置中设置了context.set_context(save_graphs=True),运行时会输出一些图编译过程中生成的一些中间文件,我们称为IR文件。当前主要有三种格式的IR文件:
ir后缀结尾的IR文件:一种比较直观易懂的以文本格式描述模型结构的文件,可以直接用文本编辑软件查看。在下文中我们也将介绍此文件的查看方式。
dat后缀结尾的IR文件:一种相对于ir后缀结尾的文件格式定义更为严谨的描述模型结构的文件,包含的内容更为丰富,可以直接用文本编辑软件查看。
dot后缀结尾的IR文件:描述了不同节点间的拓扑关系,可以用graphviz将此文件作为输入生成图片,方便用户直观地查看模型结构。对于算子比较多的模型,推荐使用可视化组件MindInsight对计算图进行可视化。
文法定义
ANF是函数式编程中常用且简洁的中间表示,其文法定义如下所示:
<aexp> ::= NUMBER | STRING | VAR | BOOLEAN | PRIMOP
| (lambda (VAR …) <exp>)
<cexp> ::= (<aexp> <aexp> …)
| (if <aexp> <exp> <exp>)
<exp> ::= (let ([VAR <cexp>]) <exp>) | <cexp> | <aexp>
ANF中表达式分为原子表达式(aexp)和复合表达式(cexp),原子表达式表示一个常数值或一个变量或一个匿名函数;复合表达式由多个原子表达式复合组成,表示一个匿名函数或原语函数调用,组合的第一个输入是调用的函数,其余输入是调用的参数。
MindIR文法继承于ANF,其定义如下所示:
<ANode> ::= <ValueNode> | <ParameterNode>
<ParameterNode> ::= Parameter
<ValueNode> ::= Scalar | Named | Tensor | Type | Shape
| Primitive | MetaFuncGraph | FuncGraph
<CNode> ::= (<AnfNode> …)
<AnfNode> ::= <CNode> | <ANode>
MindIR中的ANode对应于ANF的原子表达式,ANode有两个子类分别为ValueNode和ParameterNode。ValueNode表示常数节点,可承载一个常数值(标量、符号、张量、类型、维度等),也可以是一个原语函数(Primitive)或一个元函数(MetaFuncGraph)或一个普通函数(FuncGraph),因为在函数式编程中函数定义本身也是一个值。ParameterNode是参数节点,表示函数的形参。
MindIR中CNode对应于ANF的复合表达式,表示一次函数调用。
在MindSpore自动微分时,会计算ParameterNode和CNode的梯度贡献,并返回最终ParameterNode的梯度,而不计算ValueNode的梯度。
示例
下面以一段程序作为示例,对比理解MindIR。
def func(x, y):
return x / y
@ms_function
def test_f(x, y):
a = x - 1
b = a + y
c = b * func(a, b)
return c
这段Python代码对应的ANF表达为:
lambda (x, y)
let a = x - 1 in
let b = a + y in
let func = lambda (x, y)
let ret = x / y in
ret end in
let %1 = func(a, b) in
let c = b * %1 in
c end
对应的MindIR为ir.dot:
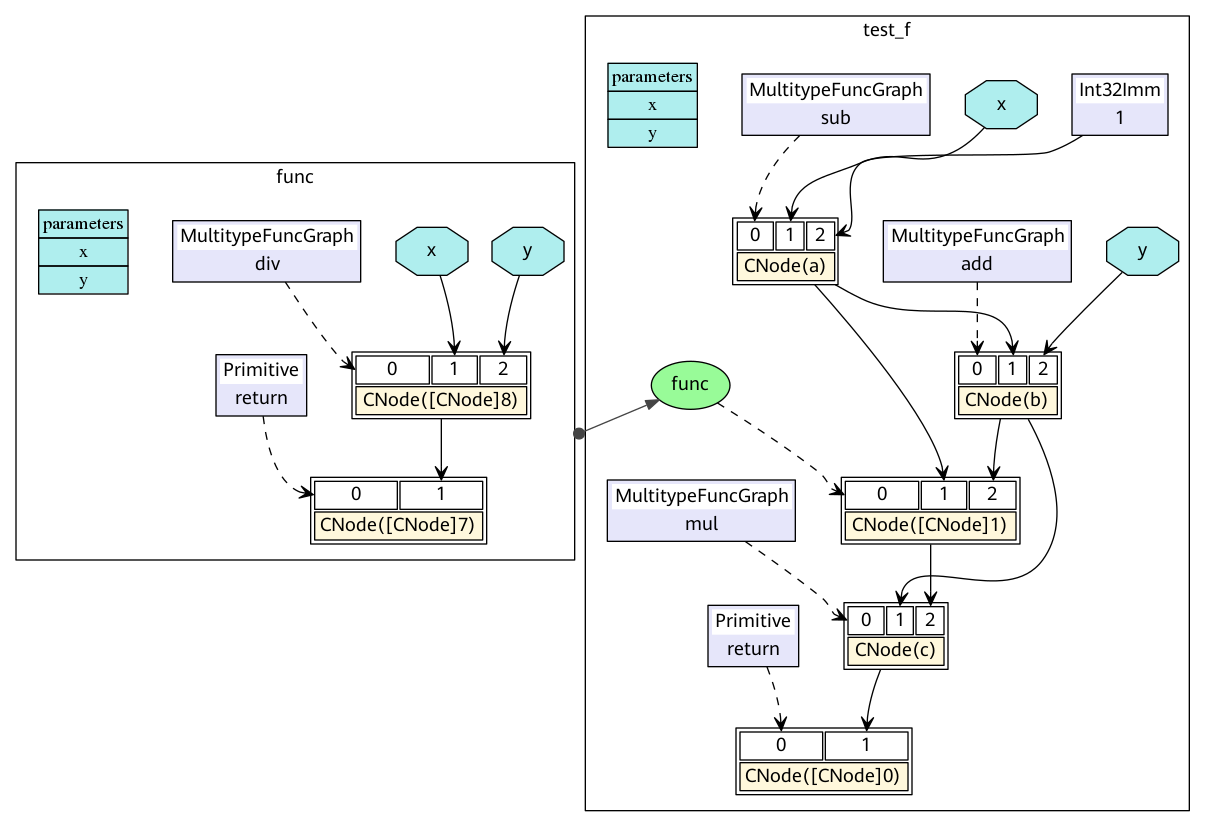
在MindIR中,一个函数图(FuncGraph)表示一个普通函数的定义,函数图一般由ParameterNode、ValueNode和CNode组成有向无环图,可以清晰地表达出从参数到返回值的计算过程。在上图中可以看出,python代码中两个函数test_f和func转换成了两个函数图,其参数x和y转换为函数图的ParameterNode,每一个表达式转换为一个CNode。CNode的第一个输入链接着调用的函数,例如图中的add、func、return。值得注意的是这些节点均是ValueNode,因为它们被理解为常数函数值。CNode的其他输入链接这调用的参数,参数值可以来自于ParameterNode、ValueNode和其他CNode。
在ANF中每个表达式都用let表达式绑定为一个变量,通过对变量的引用来表示对表达式输出的依赖,而在MindIR中每个表达式都绑定为一个节点,通过节点与节点之间的有向边表示依赖关系。
如何保存IR
通过context.set_context(save_graphs=True)来保存各个编译阶段的中间代码。被保存的中间代码有两种格式,一个是后缀名为.ir的文本格式,一个是后缀名为.dot的图形化格式。当网络规模不大时,建议使用更直观的图形化格式来查看,当网络规模较大时建议使用更高效的文本格式来查看。
DOT文件可以通过graphviz转换为图片格式来查看,例如将dot转换为png的命令是dot -Tpng *.dot -o *.png。
在训练脚本train.py中,我们在set_context函数中添加如下代码,运行训练脚本时,MindSpore会自动将编译过程中产生的IR文件存放到指定路径。
if __name__ == "__main__":
context.set_context(save_graphs=True, save_graphs_path="path/to/ir/files")
此处为单机版本的训练脚本。当运行的脚本使用多个计算设备时,MindSpore会为每一个计算设备生成一个独立的进程。因此我们建议用户在多卡版本的训练脚本中读取当前的计算设id,从而为每个设备设置独立的save_graphs_path实现将每个设备的IR文件保存在不同的路径下。例如:
device_id = os.getenv("DEVICE_ID")
context.set_context(save_graphs=True, save_graphs_path="path/to/ir/files"+device_id)
执行训练命令后,在指定的目录生成如下文件。其中以数字下划线开头的IR文件是在ME编译图过程中输出的,pipeline各阶段分别会保存一次计算图。下面介绍比较重要的阶段,例如parse阶段会解析入口的construct函数;symbol_resolve阶段会递归解析入口函数直接或间接引用到的其他函数和对象;abstract_specialize阶段会做类型推导和shape推导;optimize阶段主要是进行和硬件无关的优化,自动微分与自动并行功能也是在该阶段展开;validate阶段会校验编译出来的计算图;task_emit阶段将计算图传给后端进一步处理;execute阶段会执行该计算图。
.
├── 00_parse_[xxxx].ir
├── 00_parse.dat
├── 00_parse.dot
├── 01_symbol_resolve_[xxxx].ir
├── 01_symbol_resolve.dat
├── 01_symbol_resolve.dot
├── 02_combine_like_graphs_[xxxx].ir
├── 02_combine_like_graphs.dat
├── 02_combine_like_graphs.dot
├── 03_inference_opt_prepare_[xxxx].ir
├── 03_inference_opt_prepare.dat
├── 03_inference_opt_prepare.dot
├── 04_abstract_specialize_[xxxx].ir
├── 04_abstract_specialize.dat
├── 04_abstract_specialize.dot
├── 05_inline_[xxxx].ir
├── 05_inline.dat
├── 05_inline.dot
├── 06_py_pre_ad_[xxxx].ir
├── 06_py_pre_ad.dat
├── 06_py_pre_ad.dot
├── 07_pipeline_split_[xxxx].ir
├── 07_pipeline_split.dat
├── 07_pipeline_split.dot
├── 08_optimize_[xxxx].ir
├── 08_optimize.dat
├── 08_optimize.dot
├── 09_py_opt_[xxxx].ir
├── 09_py_opt.dat
├── 09_py_opt.dot
├── 10_validate_[xxxx].ir
├── 10_validate.dat
├── 10_validate.dot
├── 11_task_emit_[xxxx].ir
├── 11_task_emit.dat
├── 11_task_emit.dot
├── 12_execute_[xxxx].ir
├── 12_execute.dat
├── 12_execute.dot
...
IR文件内容介绍
下面以一个简单的例子来说明IR文件的内容,执行以下一段训练代码:
import mindspore.context as context
import mindspore.nn as nn
from mindspore import Tensor
from mindspore import dtype as mstype
context.set_context(mode=context.GRAPH_MODE, device_target="Ascend")
context.set_context(save_graphs=True, save_graphs_path="./ir_files")
class Net(nn.Cell):
def __init__(self):
super().__init__()
def construct(self, x, y):
x = x + y
x = x * y
return x
x = Tensor(3, mstype.float32)
y = Tensor(2, mstype.float32)
net = Net()
out = net(x, y)
print(out)
使用文本编辑软件(例如vi)打开执行完后输出的IR文件12_execute_[xxxx].ir,内容如下所示:
1 #IR entry : @6_5_1_construct_wrapper.15
2 #attrs :
3 check_set_strategy_valid_once_only : 1
4 #Total params : 2
5
6 %para1_x : <Tensor[Float32]x[const vector][]>
7 %para2_y : <Tensor[Float32]x[const vector][]>
8
9 #Total subgraph : 1
10
11 subgraph attr:
12 check_set_strategy_valid_once_only : 1
13 subgraph @6_5_1_construct_wrapper.15() {
14 %0([CNode]8) = Add(%para1_x, %para2_y) primitive_attrs: {output_names: [output], input_names: [x, y]}
15 : (<Tensor[Float32]x[const vector][]>, <Tensor[Float32]x[const vector][]>) -> (<Tensor[Float32]x[const vector][]>)
16 # In file /home/workspace/mindspore/mindspore/ops/composite/multitype_ops/add_impl.py(129)/ return F.add(x, y)/
17 # In file demo.py(14)/ x = x + y/
18 %1([CNode]10) = Mul(%0, %para2_y) primitive_attrs: {output_names: [output], input_names: [x, y]}
19 : (<Tensor[Float32]x[const vector][]>, <Tensor[Float32]x[const vector][]>) -> (<Tensor[Float32]x[const vector][]>)
20 # In file /home/workspace/mindspore/mindspore/ops/composite/multitype_ops/mul_impl.py(48)/ return F.tensor_mul(x, y)/
21 # In file demo.py(15)/ x = x * y/
22 return(%1)
23 : (<Tensor[Float32]x[const vector][]>)
24 }
以上内容可分为两个部分,第一部分为输入列表,第二部分为图结构。 其中第1行告诉了我们该网络的顶图名称@6_5_1_construct_wrapper.15,也就是入口图。 第4行告诉了我们该网络有多少个输入。 第6-7行为输入列表,遵循%para[序号]_[name] : <[data_type]x[shape]>的格式。 第9行告诉我们该网络解析出来的子图数量。 第11-24行为图结构,含有若干节点,即CNode。该示例中只有2个节点,分别为14行的Add和18行的Mul。
CNode的信息遵循如下格式,包含节点名称、属性、输入节点、输出信息、格式、源码解析调用栈等信息,由于ANF图为单向无环图,所以这里仅根据输入关系体现节点与节点的连接关系。源码解析调用栈则体现了CNode与脚本源码之间的关系,例如第20行由第21行解析而来,而第21行能对应到脚本的x = x * y。
%[序号]([debug_name]) = [OpName]([arg], ...) primitive_attrs: {[key]: [value], ...}
: (<[输入data_type]x[输入shape]>, ...) -> (<[输出data_type]x[输出shape]>, ...)
# 源码解析调用栈
需要注意的是经过编译器的若干优化处理后,节点可能经过了若干变幻(如算子拆分、算子融合等),节点的源码解析调用栈信息与脚本可能无法完全一一对应,这里仅作为辅助手段。
函数式语义
MindIR较传统计算图的一个重要特性是不仅可以表达算子之间的数据依赖,还可以表达丰富的函数式语义。
高阶函数
在MindIR中,函数的定义是由一个子图来定义,但其本身可以是一个被传递的值,作为其他高阶函数的输入或输出。
例如下面一个简单的示例中,函数f作为参数传入了函数g,因此函数g是一个接收函数输入的高阶函数,函数f真正的调用点是在函数g内部。
@ms_function
def hof(x):
def f(x):
return x + 3
def g(function, x):
return function(x) * function(x)
res = g(f, x)
return res
对应的MindIR为hof.dot:
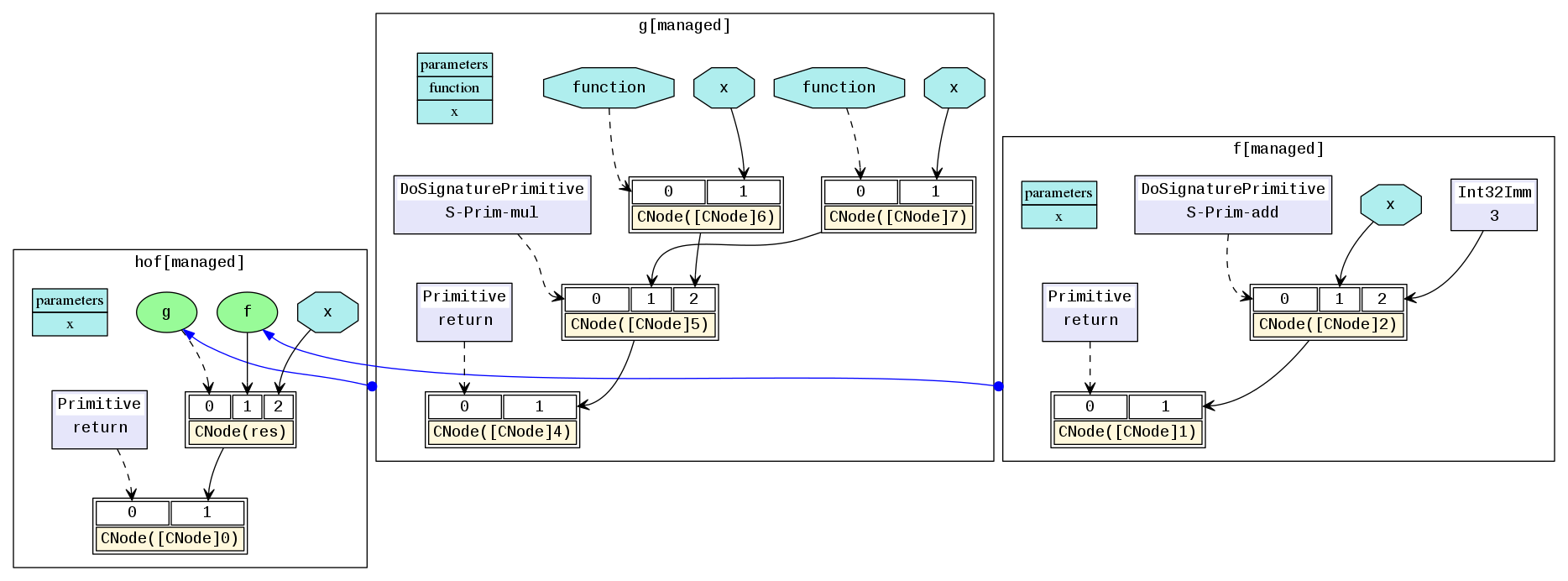
在实际网络训练脚本中,自动求导泛函GradOperation和优化器中常用到的Partial和HyperMap都是典型的高阶函数。高阶语义极大地提升了MindSpore表达的灵活性和简洁性。
控制流
控制流在MindIR中是以高阶函数选择调用的形式表达。这样的形式把控制流转换为高阶函数的数据流,从而使得自动微分算法更加强大。不仅可以支持数据流的自动微分,还可以支持条件跳转、循环和递归等控制流的自动微分。
下面以一个简单的斐波那契用例来演示说明。
@ms_function
def fibonacci(n):
if(n < 1):
return 0
elif(n == 1):
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
对应的MindIR为cf.dot:
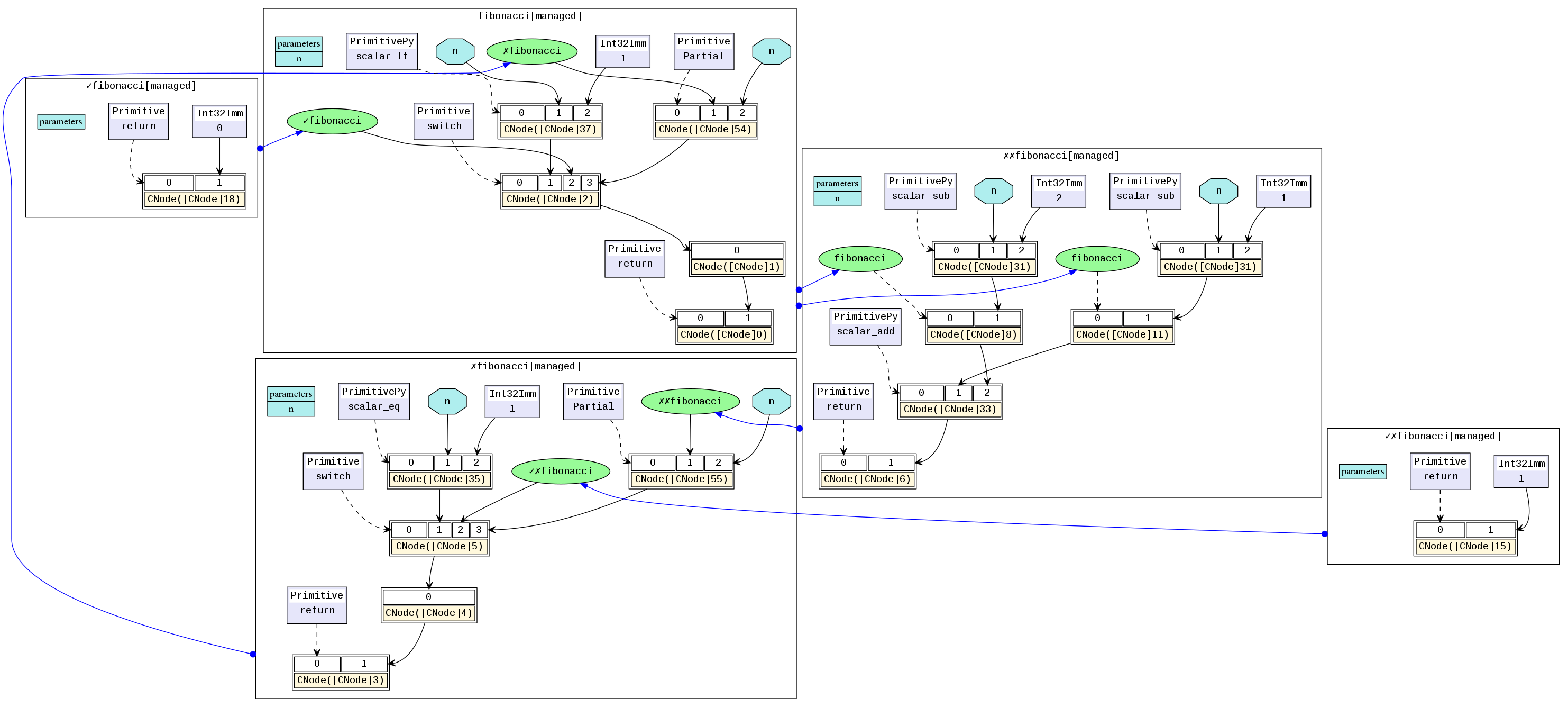
其中fibonacci是顶层函数图,在顶层中有两个函数图被switch选择调用。✓fibonacci是第一个if的True分支,✗fibonacci是第一个if的False分支。在✗fibonacci中被调用的✓✗fibonacci是elif的True分支,✗✗fibonacci是elif的False分支。这里需要理解的关键是在MindIR中,条件跳转和递归是以高阶控制流的形式表达的。例如,✓fibonacci和✗fibonacci是作为switch算子的参数传入,switch根据条件参数选择哪一个函数作为返回值。因此,switch是把输入的函数当成普通的值做了一个二元选择操作,并没有调用,而真正的函数调用是在紧随switch后的CNode上完成。
自由变量和闭包
闭包(closure)是一种编程语言特性,它指的是代码块和作用域环境的结合。自由变量(free variable)是指在代码块中引用作用域环境中的变量而非局部变量。在MindIR中,代码块是以函数图呈现的,而作用域环境可以理解为该函数被调用时的上下文环境,自由变量的捕获方式是值拷贝而非引用。
一个典型的闭包用例如下:
@ms_function
def func_outer(a, b):
def func_inner(c):
return a + b + c
return func_inner
@ms_function
def ms_closure():
closure = func_outer(1, 2)
out1 = closure(1)
out2 = closure(2)
return out1, out2
对应的MindIR为closure.dot:
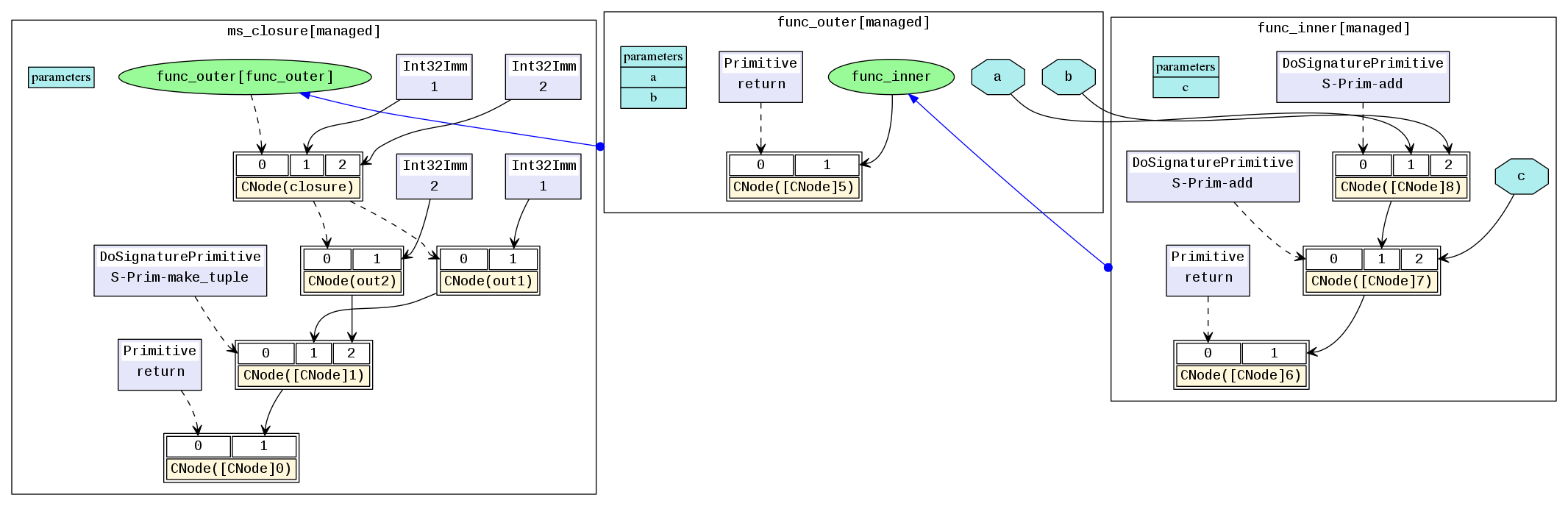
在例子中,a和b是自由变量,因为func_inner中变量a和b是引用的其父图func_outer中定义的参数。变量closure是一个闭包,它是函数func_inner与其上下文func_outer(1, 2)的结合。因此,out1的结果是4,因为其等价于1+2+1,out2的结果是5,因为其等价于1+2+2。
参考文献
[1] C. Click and M. Paleczny. A simple graph-based intermediate representation. SIGPLAN Not., 30:35–49, March 1995.
[2] Roland Leißa, Marcel Köster, and Sebastian Hack. A graph-based higher-order intermediate representation. In Proceedings of the 13th Annual IEEE/ACM International Symposium on Code Generation and Optimization, pages 202–212. IEEE Computer Society, 2015.
