mindspore.nn.GELU

class mindspore.nn.GELU(approximate=True)

Applies GELU function to each element of the input. The input is a Tensor with any valid shape.

GELU is defined as:

\[GELU(x_i) = x_i*P(X < x_i),\]

where \(P\) is the cumulative distribution function of standard Gaussian distribution and \(x_i\) is the element of the input.

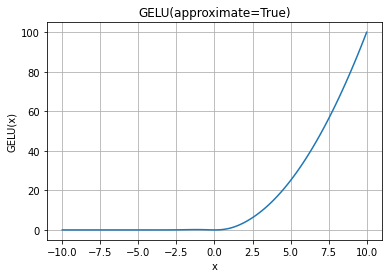
GELU Activation Function Graph:

Parameters

approximate (bool) –

Whether to enable approximation. Default: True .

If approximate is True, The gaussian error linear activation is:

\(0.5 * x * (1 + tanh(\sqrt(2 / \pi) * (x + 0.044715 * x^3)))\)

else, it is:

\(x * P(X <= x) = 0.5 * x * (1 + erf(x / \sqrt(2)))\), where P(X) ~ N(0, 1).

Inputs:

• x (Tensor) - The input of GELU with data type of float16, float32, or float64. The shape is \((N,*)\) where \(*\) means, any number of additional dimensions.

Outputs:

Tensor, with the same type and shape as the x.

Note

when calculating the input gradient of GELU with an input value of infinity, there are differences in the output of the backward between Ascend and GPU. when x is -inf, the computation result of Ascend is 0, and the computation result of GPU is Nan. when x is inf, the computation result of Ascend is dy, and the computation result of GPU is Nan. In mathematical terms, the result of Ascend has higher precision.

Raises

TypeError – If dtype of x is not one of float16, float32, or float64.

Supported Platforms:

Ascend GPU CPU

Examples

>>> import mindspore
>>> from mindspore import Tensor, nn
>>> import numpy as np
>>> x = Tensor(np.array([[-1.0, 4.0, -8.0], [2.0, -5.0, 9.0]]), mindspore.float32)
>>> gelu = nn.GELU()
>>> output = gelu(x)
>>> print(output)
[[-1.5880802e-01  3.9999299e+00 -3.1077917e-21]
 [ 1.9545976e+00 -2.2918017e-07  9.0000000e+00]]
>>> gelu = nn.GELU(approximate=False)
>>> # CPU not support "approximate=False", using "approximate=True" instead
>>> output = gelu(x)
>>> print(output)
[[-1.5865526e-01  3.9998732e+00 -0.0000000e+00]
 [ 1.9544997e+00 -1.4901161e-06  9.0000000e+00]]